Reference

Combinational Circuits in Computer Science

组合逻辑电路的分析

组合逻辑电路的定义

对于一个逻辑电路, 其输出状态在任何时候只取决于同一时刻的输入状态, 而与电路原来的状态无关, 这种电路被定义为 组合逻辑电路

组合逻辑电路的输出输出之间的逻辑关系可以用如下逻辑函数来描述

L_{i} = f (A_{1}, A_{2}, \dots, A_{n}), i = 1, 2, \dots, m

其中 $A_{1}, A_{2}, \dots, A_{n}$ 为输入变量

组合逻辑电路的结构具有如下特点

输出, 输入之间没有反馈延迟通路
电路中不含具有记忆功能的元件

组合逻辑电路的分析方法

写出逻辑函数表达式
化简逻辑表达式
列出真值表
分析真值表, 确定逻辑电路的功能

组合逻辑电路的设计

设计过程

明确逻辑功能
写出真值表
写出逻辑表达式
化简逻辑表达式

优化实现

优化电路使得成本降低, 逻辑电路的成本是由电路中总的逻辑门数量加上所有逻辑门的输入端数来表示

对于单输出门电路, 可以把与门和或门转化为与非门和或非门, 因为后者所用的三极管更少, 速度快
对于多输出电路, 可以考虑复用中间结果

多级逻辑电路

提取公因子

把

L = A BC D + A B \overset{ˉ}{C} E + A B D \overset{ˉ}{F}

转换为

L = A B (C D + \overset{ˉ}{C} E + D \overset{ˉ}{F})

组合逻辑电路中的竞争-冒险

竞争

当组合逻辑电路的输入信号发生变化时, 如果多个信号同时到达某个门电路, 并且这些信号的变化可能导致门电路的输出发生改变, 那么就可能出现竞争. 竞争本身不一定会导致错误, 但是它是冒险产生的必要条件.

考虑一个简单的与非门 (NAND) 电路, 它的输入是 $A$ 和 $\overline{A}$ . 理想情况下, 这个电路的输出应该始终为高电平 (1), 因为 $A$ 和 $\overline{A}$ 永远不会同时为高电平. 然而在实际电路中, 当 $A$ 从 0 变为 1 时, $\overline{A}$ 并不会立即从 1 变为 0, 而会有一个短暂的延迟.

假设假设反相器 (NOT) 的延迟为 $Δ t$ .

$t < 0$ 时: $A = 0$ , $\overline{A} = 1$ , NAND 输出 = 1.
$t = 0$ 时: $A$ 从 0 变为 1.
$0 < t < Δ t$ 时: $A = 1$ , $\overline{A}$ 仍然为 1 (由于反相器延迟), NAND 输出 = 0 (短暂的毛刺).
$t > Δ t$ 时: $A = 1$ , $\overline{A} = 0$ , NAND 输出 = 1.

冒险

冒险是指由于竞争而导致的输出端出现不希望的瞬时脉冲或毛刺 (glitch). 这种毛刺可能会导致后级电路误动作.

冒险的类型

静态冒险 (Static Hazard): 当输入发生变化, 理论上输出应该保持不变, 但实际上输出出现了短暂的跳变.

静态1冒险 (Static-1 Hazard): 输出应该保持为1, 但短暂变为0.
静态0冒险 (Static-0 Hazard): 输出应该保持为0, 但短暂变为1.

动态冒险 (Dynamic Hazard): 当输入发生变化, 理论上输出应该发生变化, 但输出发生了多次跳变才稳定到最终值.

检测方法

代数法 (Algebraic Method):

对于静态1冒险, 检查逻辑表达式是否可以化简为 $F = X + \overline{X}$ 的形式. 如果可以, 则可能存在静态1冒险.
对于静态0冒险, 检查逻辑表达式是否可以化简为 $F = X \cdot \overline{X}$ 的形式. 如果可以, 则可能存在静态0冒险. 卡诺图法 (Karnaugh Map Method):
对于静态1冒险, 在卡诺图中, 如果两个相邻的1之间没有被同一个圈覆盖, 则可能存在静态1冒险.
对于静态0冒险, 在卡诺图中, 如果两个相邻的0之间没有被同一个圈覆盖, 则可能存在静态0冒险. (这种情况通常在设计时避免产生0冒险) . 仿真法 (Simulation Method): 使用电路仿真软件, 输入不同的信号, 观察输出是否有毛刺.

消除方法

增加冗余项 (Adding Redundant Terms): 对于静态1冒险, 在卡诺图中, 增加一个圈来覆盖相邻的1, 对应于在逻辑表达式中增加一个冗余项.

例如, 如果表达式为 $F = A B + \overline{A} C$ , 可能存在静态1冒险 (如果 $B = C = 1$ , 无论 $A$ 取什么值, 输出均应该为 $1$ . 但是当 $A$ 从 $1$ 变成 $0$ 时, 由于 $\overset{ˉ}{A}$ 响应的延迟, 可能会导致 $\overset{ˉ}{A} C$ 项延迟变为 $1$ ). 增加冗余项 $BC$ (逻辑函数还是和原来等价), 得到 $F = A B + \overline{A} C + BC$ , 可以消除冒险.

增加滤波电容 (Adding Filtering Capacitors): 在输出端增加小的滤波电容, 可以滤除短暂的毛刺. 但是, 电容的增加会降低电路的响应速度.

选通法 (Strobing/Gating): 使用一个选通信号, 在输出稳定后才允许输出信号通过. 这会低电路的响应速度.

采用格雷码 (Using Gray Code): 在状态机设计中, 使用格雷码可以确保每次状态转换只有一个位发生变化, 从而减少竞争-冒险的发生.

同步电路设计 (Synchronous Circuit Design): 采用同步电路设计, 使用时钟信号来同步所有操作, 可以避免异步电路中出现的竞争-冒险.

常用组合逻辑电路模块

编码器

定义

具有编码功能的逻辑电路是编码器, 有 $n$ 位二进制输出, 与 $2^{n}$ 个输入相对应.

普通编码器: 任何时候只允许一个输入信号有效, 否则产生错误输出
优先编码器: 允许多个输入信号同时有效, 输出是对优先级别高的输入信号编码

普通编码器

4线-2线普通编码器是一种组合逻辑电路, 它将4个输入信号编码成2个输出信号. 编码器的主要功能是将多个输入信号中激活的信号转换成相应的二进制代码.

真值表

输入 I3	输入 I2	输入 I1	输入 I0	输出 Y1	输出 Y0
0	0	0	1	0	0
0	0	1	0	0	1
0	1	0	0	1	0
1	0	0	0	1	1
其它	其它	其它	其它	X	X

逻辑表达式 根据真值表, 可以得到输出信号的逻辑表达式:

$Y_{0} = \overline{I_{3}} \cdot \overline{I_{2}} \cdot I_{1} \cdot \overline{I_{0}} + \overline{I_{3}} \cdot I_{2} \cdot \overline{I_{1}} \cdot \overline{I_{0}} = I_{1} \overline{I_{2}} \overline{I_{3}} + I_{3} \overline{I_{2}} \overline{I_{1}}$
$Y_{1} = \overline{I_{3}} \cdot I_{2} \cdot \overline{I_{1}} \cdot \overline{I_{0}} + I_{3} \cdot \overline{I_{2}} \cdot \overline{I_{1}} \cdot \overline{I_{0}} = I_{2} \overline{I_{1}} \overline{I_{0}} \overline{I_{3}} + I_{3} \overline{I_{2}} \overline{I_{1}} \overline{I_{0}}$ 简化后的逻辑表达式:
$Y_{0} = I_{1} + I_{3}$
$Y_{1} = I_{2} + I_{3}$

优先编码器

8线-3线优先编码器是一种组合逻辑电路, 它将8个输入信号编码成3个输出信号. 与普通编码器不同, 优先编码器可以处理多个输入信号同时有效的情况. 当多个输入同时有效时, 优先编码器会选择优先级最高的输入信号进行编码, 忽略其他输入信号.

真值表

输入 I7	输入 I6	输入 I5	输入 I4	输入 I3	输入 I2	输入 I1	输入 I0	输出 Y2	输出 Y1	输出 Y0	有效输出(GS)
0	0	0	0	0	0	0	0	X	X	X	0
0	0	0	0	0	0	0	1	0	0	0	1
0	0	0	0	0	0	1	X	0	0	1	1
0	0	0	0	0	1	X	X	0	1	0	1
0	0	0	0	1	X	X	X	0	1	1	1
0	0	0	1	X	X	X	X	1	0	0	1
0	0	1	X	X	X	X	X	1	0	1	1
0	1	X	X	X	X	X	X	1	1	0	1
1	X	X	X	X	X	X	X	1	1	1	1

说明:

I0, I1, I2, I3, I4, I5, I6, I7 是输入信号, 代表8根输入线. I7 的优先级最高, I0 的优先级最低.
Y0, Y1, Y2 是输出信号, 代表3根输出线, 输出的是优先级最高的有效输入信号的二进制编码.
GS (有效输出) 指示信号, GS=1时, 表示至少有一个输入有效; GS=0时, 表示所有输入都无效 (都为0) .
X 表示无关项, 即该输入可以是0或1, 不影响输出结果.

译码器

译码就是编码的逆过程

二进制译码器

接收一个 $n$ 位的二进制输入, 并激活 $2^{n}$ 条输出线中对应于该输入数值的一条

使能端:

为高电平时, 译码器正常工作
为低电平时, 所有输出都为低电平

十进制译码器

七段显示译码器

数据分配器

相当于多个输出的单刀多掷开关, 把公共数据线上的数据根据需要送到不同的通道上去, 实现数据分配的功能.

数据分配器可以用带 使能端 的二进制译码器实现

译码器的每条输出线都可以作为数据分配器的一个输出通道
译码器的二进制输入线用作数据分配器的选择线, 这些选择线决定了哪个输出通道将被激活
将数据分配器的输入数据线连接到译码器的使能端

数据选择器

从多个输入信号中选择一个信号进行输出的器件

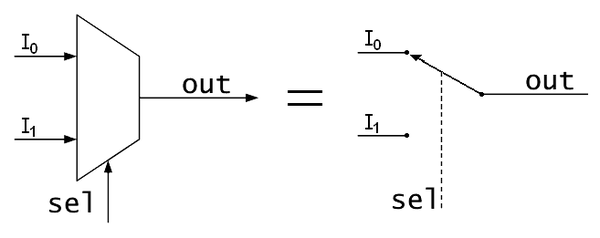
数值比较器

对两个二进制数 $A$ , $B$ 进行比较, 结果有 $A > B$ , $A < B$ 和 $A = B$ 三种情况

Lin's Notes Garden

Explorer

Combinational Logics Circuits