General Methods to Analyze Resistive Circuits

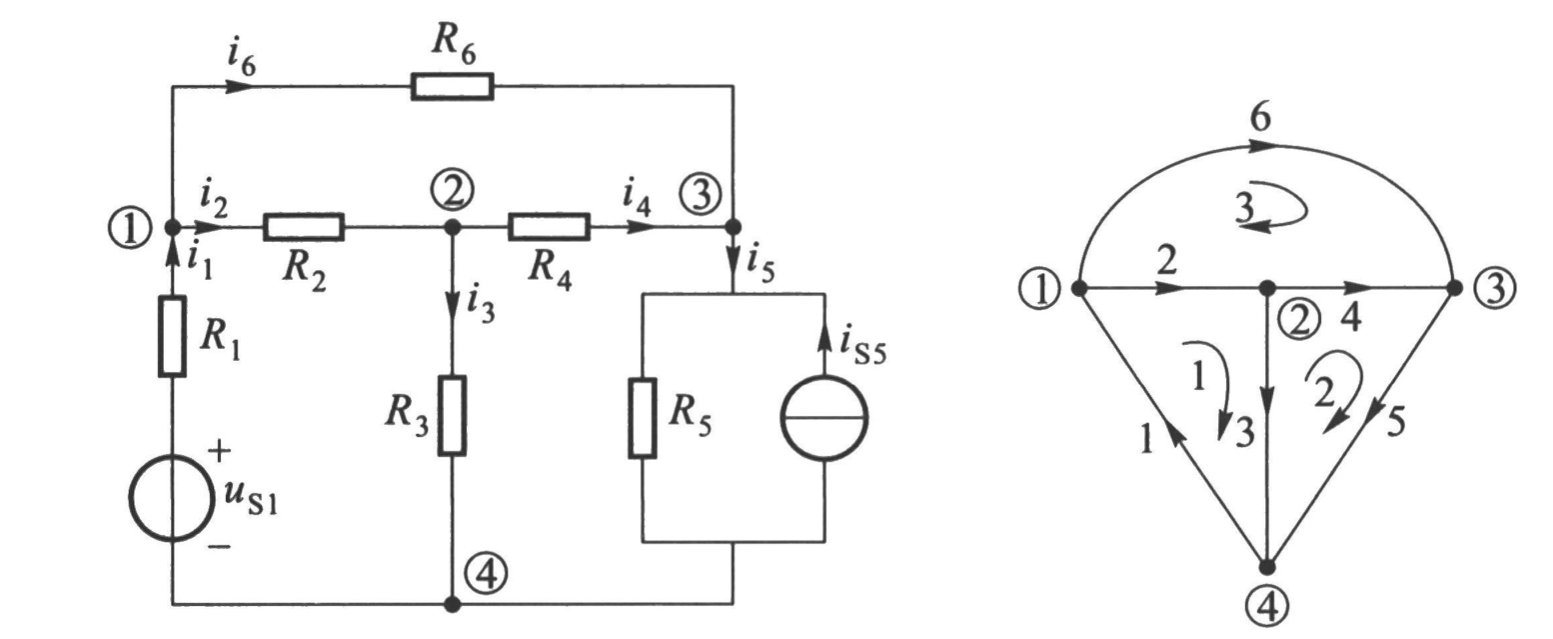
Branch Current Method

This method involves defining and calculating the current in each branch of the circuit. A branch is any part of a circuit with a unique current. For a circuit with $n$ nodes and $b$ branches:

1. Assigning a current variable to each branch.
2. Applying KCL at each node to account for the sum of currents entering and leaving the node. ($n-1$ equations)
3. Applying KVL to each loop or closed path to ensure that the sum of voltages around the loop equals zero. ($b-n+1$ equations) This method is general but can become cumbersome for circuits with many branches.

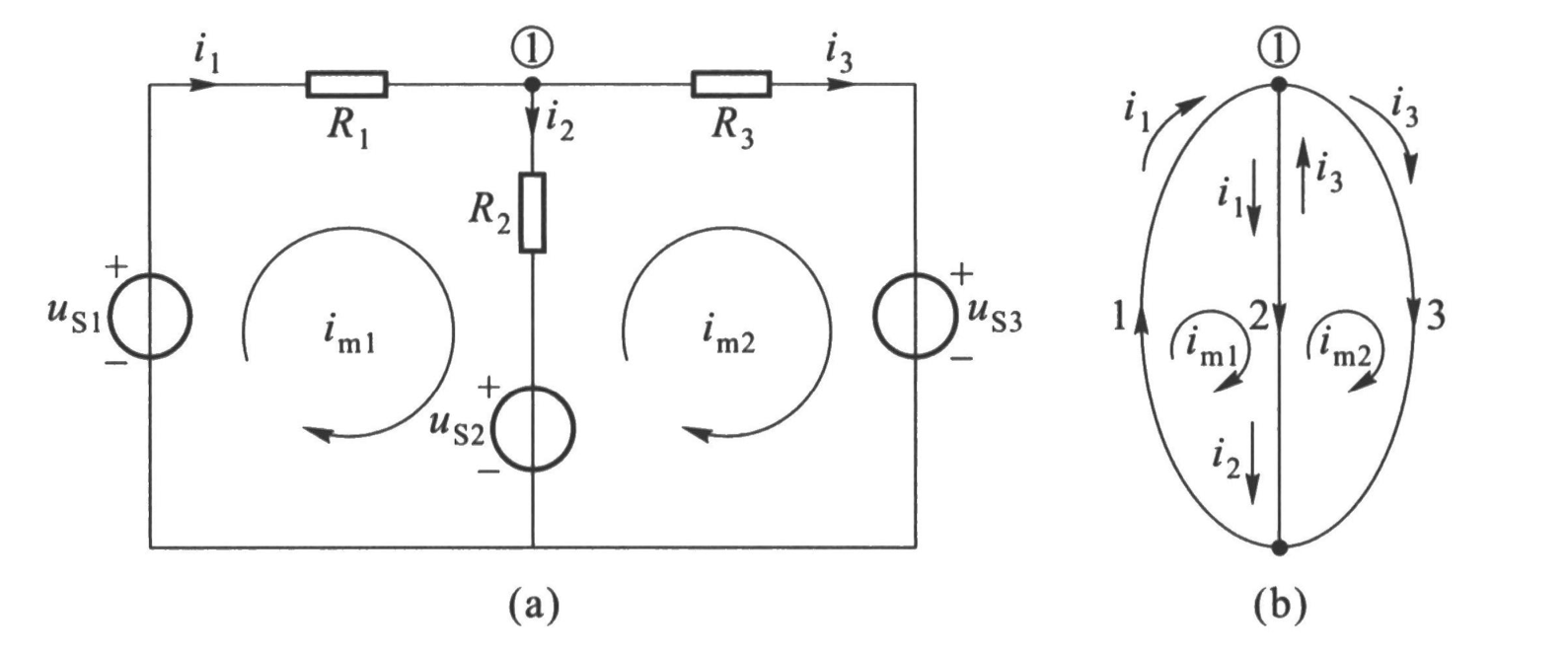
Mesh Current Method

The mesh current method is a simplification of the branch current method and is typically used for planar circuits (circuits that can be drawn on a plane without crossing wires). The process involves:

1. Identifying the meshes (loops that do not contain other loops) in the circuit.
2. Assigning a current variable to each mesh.
3. Applying KVL to each mesh to form equations based on the sum of voltage drops.
4. Solving the resulting system of equations to find the mesh currents. This method reduces the number of unknowns since each mesh is treated as a single current, instead of each branch having its own.

Tip

When a branch contains only a current source without any parallel resistance, the branch voltage cannot be expressed in terms of the branch current. Such a current source without parallel resistance is called a unattended current source.

In the mesh analysis method, there are two ways to handle unattended current sources:

1. When a unattended current source is present in only one mesh, the current of the current source can be considered as the current of that mesh.
2. When a unattended current source is located on a common branch of two meshes, the voltage at the terminals of the unattended current source can be treated as an unknown variable (referred to as the auxiliary variable method), and an additional mesh current equation describing the unattended current source should be added.

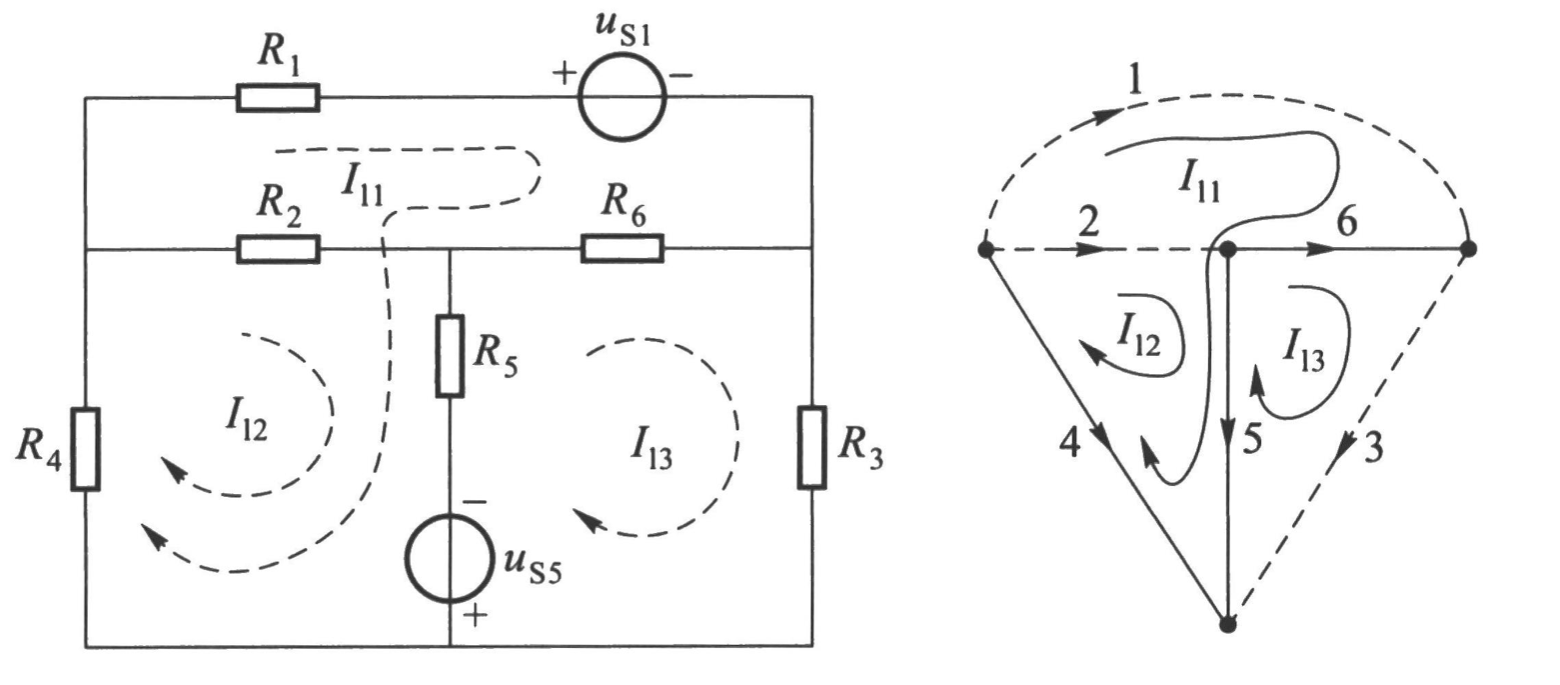
Loop Current Method

The loop current method is similar to the mesh current method but applies to both planar and non-planar circuits. In this method:

1. Loops are defined in the circuit, and a current variable is assigned to each loop.
2. KVL is applied to each loop to generate equations.
3. The equations are solved for the loop currents. In non-planar circuits, there may be more loops than meshes, leading to more variables compared to the mesh current method.

Node Voltage Method

The node voltage method analyzes circuits by focusing on the voltages at the circuit's nodes. This method is particularly efficient for planar circuits and can handle circuits with voltage sources, resistors, and other elements.

1. Nodes Identification: Identify all the nodes in the circuit, and choose a reference node (often referred to as the ground). Assign voltage variables to the remaining nodes.
2. KCL Application: Apply Kirchhoff' s Current Law (KCL) at each non-reference node. This results in equations that express the current in terms of node voltages and element values.
3. Solve the Equations: Use the system of equations to solve for the unknown node voltages. This method reduces the number of variables in comparison to the loop current method, as it focuses on node voltages rather than loop currents. It is especially advantageous when dealing with circuits that contain a large number of nodes but relatively fewer components.