Geometric Laplace Transform Analysis

几何分析方法

信号的 Fourier变换 就是沿 $j\omega$ 轴对其 Laplace变换 的求值. 本节讨论了一种利用与有理拉普拉斯变换相关的零极点图来求解傅里叶变换, 以及更一般地求解拉普拉斯变换在任意点 $s$ 处的值的方法.

为了建立这种方法, 让我们首先考虑只有一个零点的拉普拉斯变换 (即 $X(s)=(s-a)$) 在给定点 $s$ 处的求值, 例如 $s=s_1$. 代数表达式 $s_1-a$ 是两个复数的和, 一个是 $s_1$, 另一个是 $-a$: 每个都可以在复平面中表示为一个向量.

因此, $X(s_1)$ 的幅值就是这个向量的长度, 而相位是这个向量相对于实轴的角度. 如果 $X(s)$ 在 $s=a$ 处有一个极点, 即 $X(s)=1/(s-a)$, 那么 $X(s)$ 的分母就是上面讨论的同一个向量. 在这种情况下, $X(s_1)$ 的幅值是该向量长度（从极点 $s=\alpha$ 到点 $s=s_1$）的倒数, 而相位是该向量相对于实轴的角度的负值.

一个更一般的有理拉普拉斯变换由零点和极点项的乘积组成. 也就是说, 有理拉普拉斯变换可以分解为:

$$X(s)=M\frac{{\prod }_{i=1}^R(s-{\beta }_i)}{{\prod }_{j=1}^P(s-{\alpha }_j)}$$

为了求出 $X(s)$ 在 $s=s_1$ 处的值, 乘积中的每一项都可以表示为从零点或极点到点 ${\sigma }_l$ 的向量. 然后, $X(s_1)$ 的幅值是 $M$ 乘以所有零点向量（从每个零点到 $s_1$ 的向量）长度的乘积, 再除以所有极点向量（从每个极点到 $s_1$ 的向量）长度的乘积. 复数 $X(s_1)$ 的相位角是所有零点向量的相位角之和减去所有极点向量的相位角之和.

如果比例因子 $M$ 为负, 则会有一个额外的 $\pi$ 相位角. 如果 $X(s)$ 有重极点或重零点（或两者都有）, 即如果某些 ${\alpha }_i$ 和/或 ${\beta }_i$ 相等, 那么这些重极点或重零点的向量长度和相位角应该在 $X(s_1)$ 中以相应的重数（等于极点或零点的阶数）包含进去.

一阶系统

现在考虑一阶系统. 这类系统的单位冲激响应是

$$h(t)=\frac{1}{\tau }{\mathrm{e}}^{-t/\tau }u(t)$$

它的拉普拉斯变换就是

$$H(s)=\frac{1}{s\tau +1},\mathcal{R}e\{s\}>-\frac{1}{\tau }$$

其零-极点图如图1所示. 从该图可以看到, 极点向量的长度在 $\omega =0$ 最短, 并随 $\omega$ 增加而单调增加；同时, 极点向量的相角随 $\omega$ 从0增加到 $\infty$ 而单调地从0增加到 $\pi /2$ .

从极点向量随 $\omega$ 变化的规律来看, 很明显其频率响应 $H(j\omega )$ 的模随 $\omega$ 增加而单调下降, 而 $\sphericalangle H(j\omega )$ 则单调地从0下降到 $-\pi /2$ , 如该系统的伯德图所示. 同时也注意到, 当 $\omega =1/\tau$ 时, 极点向量的实部和虚部相等, 从而频率响应的模从它在 $\omega =0$ 时的最大值下降了 $1/\sqrt{2}$ , 或近似下降3 dB;而此时频率响应的相位是 $\pi /4$ 值. 这与6.5.1节讨论一阶系统时所得结论相一致, 在那里就将 $\omega =1/\tau$ 称为3dB点或转折频率, 也就是I $H(j\omega )$ 1伯德图的直线近似在斜率上有一个转折处的频率. 时间常数控制了一阶系统的响应速度, 这样一个系统在 $s=-1/\tau$ 的极点在负实轴上, 它到原点的距离就是该时间常数的倒数.
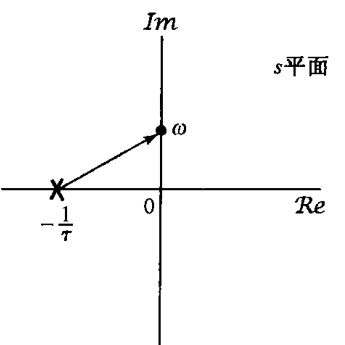图1 一阶系统的零-极点图

从图示效果也能看到, 时间常数, 或者等效地说 $\begin{array}{r}H(s)\end{array}$ 极点位置的变化如何改变一阶系统的特性. 特别是, 极点越朝左半平面移, 系统的转折频率, 或有效截止频率就会增加；同时, 极点向左移动对应于时间常数 $\tau$ 的减小, 结果单位冲激响应就衰减得更快, 而阶跃响应则有一个更快的上升时间. 极点位置的实部和系统响应速度之间的这一关系一般总是成立的, 即远离 $j\omega$ 轴的那些极点, 总是对应于单位冲激响应中的那些快速响应项.
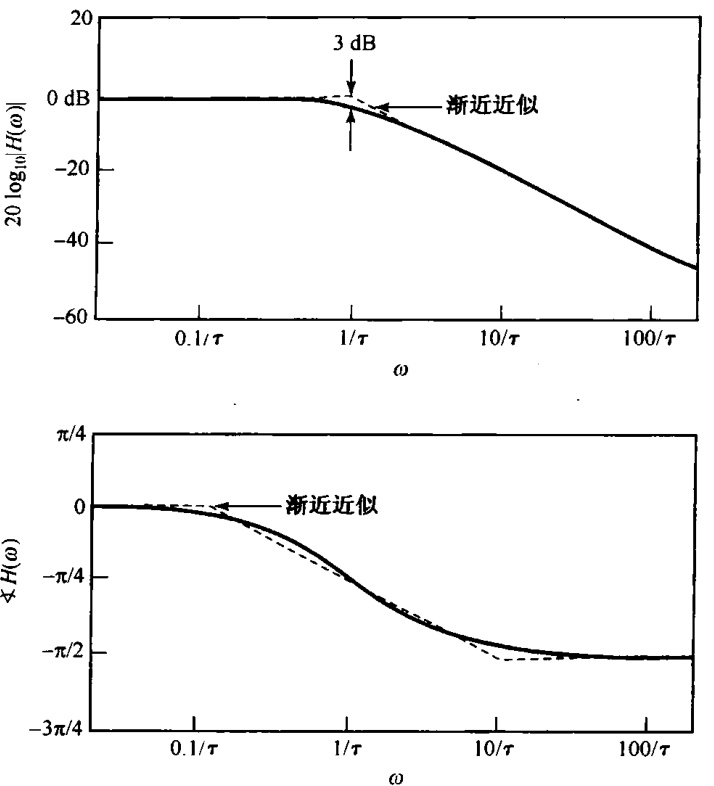图2 一阶系统的频率响应

二阶系统

下面来讨论二阶系统, 对于这类系统的单位冲激响应和频率响应

$$h(t)=M[{\mathrm{e}}^{c_{1}t}-{\mathrm{e}}^{c_{2}t}]u(t)$$

其中,

$$\begin{array}{l}{c}_1=-\xi {\omega }_n+{\omega }_n\sqrt{{\zeta }^2-1}\\ c_2=-\zeta {\omega }_n-{\omega }_n\sqrt{{\zeta }^2-1}\\ M=\frac{{\omega }_n}{2\sqrt{{\zeta }^2-1}}\end{array}$$

且

$$H(j\omega )=\frac{{\omega }_n^2}{(j\omega {)}^2+2\zeta {\omega }_n(j\omega )+{\omega }_n^2}$$

单位冲激响应的拉普拉斯变换是

$$H(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}=\frac{{\omega }_n^2}{(s-c_1)(s-c_2)}$$