Mathematical Model for Control Systems

时域模型

例子

弹簧-质量-阻尼器机械位移系统

$$m\ddot{x}=F(t,x,\dot{x})⟹m\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}+f\frac{\mathrm{d}x}{\mathrm{d}t}+Kx(t)=F(t)$$

RLC串联系统

...

标准形式

• 系数转化为时间常数
• 与输出有关的放在左边, 与输入有关的放在右边
• 按照求导阶数降序排列

$$T_1{T}_2\frac{{\mathrm{d}}^{2}x}{\mathrm{d}{t}^2}+T_2\frac{\mathrm{d}x}{\mathrm{d}t}+x(t)=F(t)$$

这里$T_1,T_2$的量纲为时间.

例如对于RLC串联系统, 可以为$T_1=L/R,T_2=RC$.

标准形式的微分方程

$$a_0\frac{{\mathrm{d}}^{n}c}{\mathrm{d}{t}^n}+a_1\frac{{\mathrm{d}}^{n-1}c}{\mathrm{d}{t}^{n-1}}+\cdots +a_{n-1}\frac{\mathrm{d}c}{\mathrm{d}t}+a_{n}c=b_0\frac{{\mathrm{d}}^{m}r}{\mathrm{d}{t}^m}+b_1\frac{{\mathrm{d}}^{m-1}r}{\mathrm{d}{t}^{m-1}}+\cdots +b_{m-1}\frac{\mathrm{d}r}{\mathrm{d}t}+b_{m}r$$

满足如下约束

• 系数都为实数
• 一般有$n>m$, 因为实际物理系统都具有惯性
• 左右两边的量纲是一致的

这描述了一个线性系统, 具有如下性质

• 叠加性: 可以相加
• 齐次性: 可以做缩放

非线性模型

线性化方法

• 忽略弱线性的环节
• Taylor系数展开
• 平均斜率法

$s$域模型

复习: Laplace Transform

• Final Value Theorem 求留数的方法:
• 一次分母
• 高次分母（把第次留数项直接减掉, 或者求导）

传递函数：单输入单输出线性定常动态对象的传递函数$G(s)$是零初值条件下该对象的输出量的Laplace变换$C(d)$和输入量的Laplace变换$R(s)$之比

$$G(s)=\frac{C(s)}{R(s)}$$

给定传递函数, 无论输入如何, 系统都以相同的传递作用输出信息或能量

传递函数的性质

• 传递函数和微分方程等价
• 和输入量无关
• 只适用于线形定常（Linear Time-Invariant Systems (LTI)）系统
• 不反映中间变量具体的传递关系, 只描述输入和输出之间的关系
• 一般为复变量$s$的有理实分式, 期中分母多项式是系统的特征多项式, 决定系统的动态性能 (极点决定了系统固有的运动属性)
• 在零初始条件下定义, 因此只能反应零状态响应
• 传递函数是系统单位冲激响应的Laplace变换

零-极点图

复习 Pole-Zero Plot

运动模态

$C(s)=\frac{s+6}{(s+1)(s^2+4s+5)}=\frac{5}{2}\cdot \frac{1}{s+1}-\frac{5}{2}\cdot \frac{s+2}{(s+2{)}^2+1}-\frac{3}{2}\cdot \frac{1}{(s+2{)}^2+1}$ 对应的时间域函数为 $c(t)=\frac{5}{2}{e}^{-t}-\frac{5}{2}{e}^{-2t}\cos t-\frac{3}{2}{e}^{-2t}\sin t$

自由运动的三种模态, 取决于对应的三个特征根

运动模态：一般来说, 如果微分方程的特征根是${\lambda }_1{\lambda }_2$ ……, ${\lambda }_n$ (无重复), 则函数$\exp ({\lambda }_{1}t),\exp ({\lambda }_{2}t),\dots ,\exp ({\lambda }_{n}t)$被定义为方程的运动模态.

如果特征根中有共轭复根$\sigma \pm j\omega$, 则共轭复模态可以写成$e^{\sigma t}\cos \omega$和$e^{\sigma t}\sin \omega t$.

如果特征根中有重根, 则模态将具有$t^k{e}^{\lambda t}$、$t^k{e}^{\sigma t}\cos \omega t$、$t^k{e}^{\sigma t}\cos \omega$的形式

极点位置决定模态的收敛性/稳定性: 当极点具有负实部或为负实数时, 对应运动模态是收敛的 ($\exp (\lambda t)$在$t\to \infty$时衰减到$0$). 稳定性问题完全取决于极点的位置, 在零极点分布图上, 全部极点在左半平面, 系统即稳定. 极点距离虚轴越远, 相应模态收敛越快

零点决定运动模态的比重: 若零点靠近某极点, 则该极点的对应模态比重会减小；当零极点对消时, 相应模态消失

两种形式的传递系数

传递系数决定了系统稳态的传递性能：稳态输出与输入成比例关系 设

$$\begin{array}{rl}G(s)& =\frac{b_0{s}^m+\cdots +b_{m-1}s+b_m}{a_0{s}^n+\cdots +a_{n-1}s+a_n}\\ & =K_g\frac{(s-z_1)\cdots (s-z_m)}{(s-p_1)\cdots (s-p_n)}\end{array}$$

其中

• 根轨迹增益 $K_g=\frac{b_0}{a_0}$
• 静态放大倍数（静态增益）$K={\lim }_{s\to 0}G(s)=\frac{b_m}{a_n}=\frac{K_g{\prod }_{i=1}^m(-z_i)}{{\prod }_{j=1}^n(-p_j)}$ 设系统输入为$r(t)=u_0\cdot 1(t)$, 则由终值定理得稳态输出为

$$\underset{t\to \infty }{\lim }c(t)=\underset{s\to 0}{\lim }sG(s)\frac{u_0}{s}=G(0)u_0=K{u}_0$$

结构图和信号流图

结构图

由具有一定函数关系的环节组成的，并标明信号流向的系统的方框图，称为系统的结构图

开环和闭环系统的结构图

闭环系统的传递函数

$$\frac{G(s)}{1+G(s)H(s)}$$

$G(s)$正向传递, $H(s)$反馈传递

结构图的等效变换

复杂结构图的化简

信号流图

信号流图是表示一组联立线性代数方程的图，由节点表示变量、 由支路表示传输（增益），可表达变量之间的信号传递关系、函数运算关系和变量因果关系

• 源点: 只有输出支路的节点称为源点或称为输入节点
• 汇点: 只有输入支路的节点称为汇点或称为输出节点
• 混合节点: 既有输入支路又有输出支路的节点称混合节点

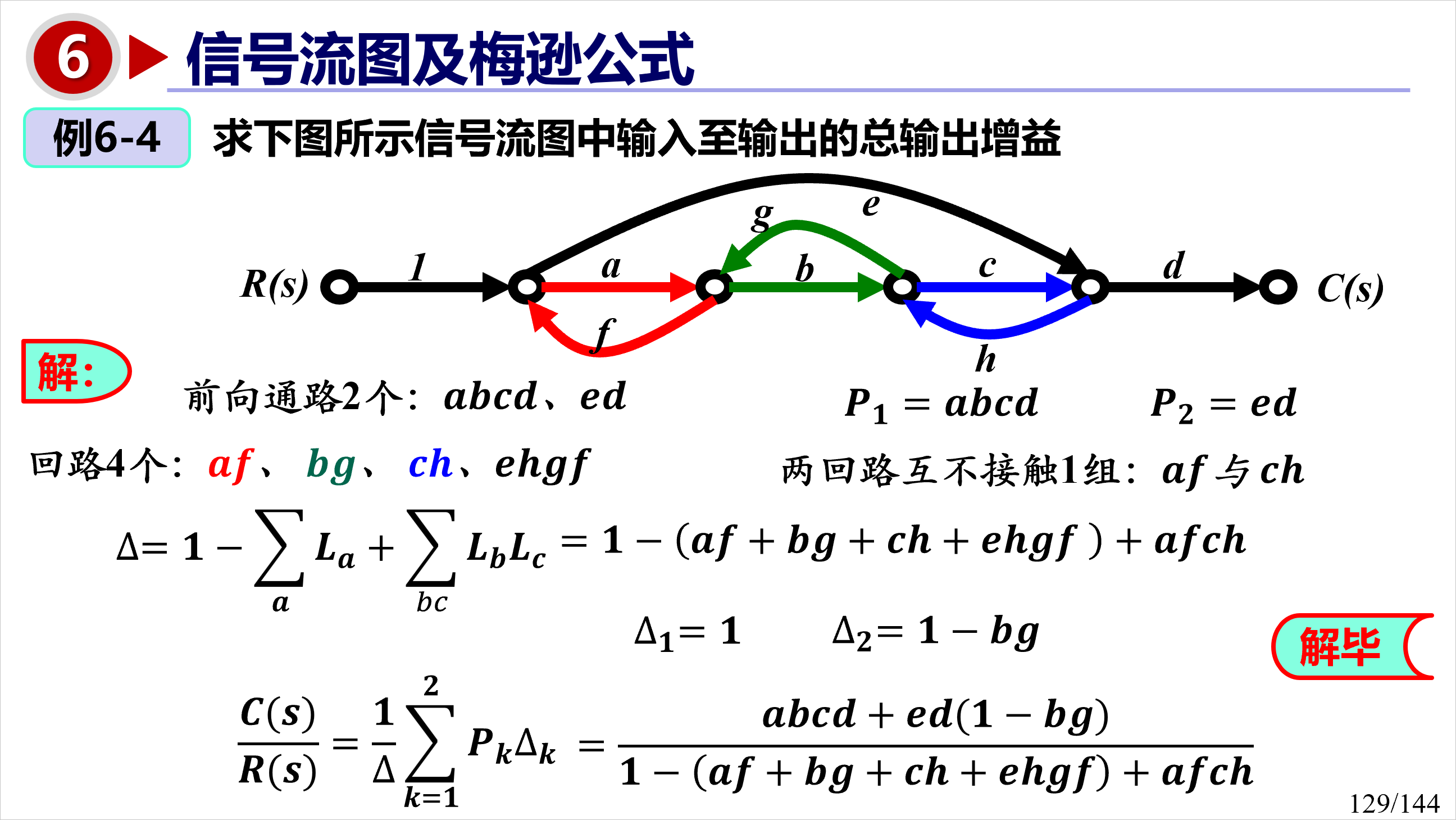
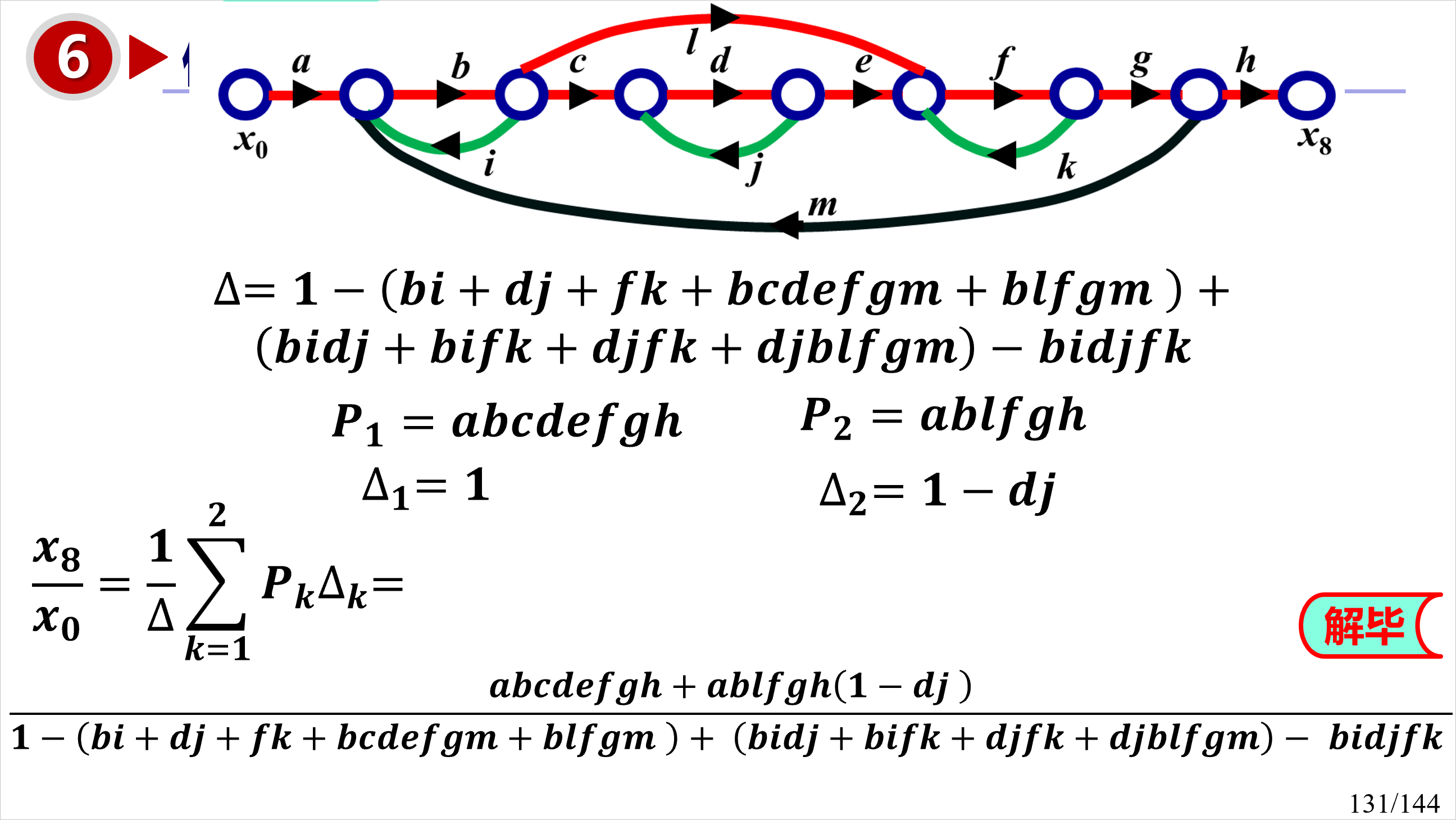
梅逊增益公式

对于一个信号流图，系统的传递函数 $T$ 可以表示为：

$$T=\frac{{\sum }_k{P}_k{\Delta }_k}{\Delta }$$

其中：

• $P_k$ 是第 $k$ 条前向路径的增益。
• $\Delta$ 是系统的行列式（determinant），计算公式为：

$$\Delta =1-\sum L_i+\sum L_i{L}_j-\sum L_i{L}_j{L}_k+\cdots +(-1{)}^m\sum \cdots$$

• $L_1$ 是单个环路的增益之和(这里的环路不能再被拆分成更小的环路, 也就是说这个环路的任意真子图都不能构成一个环路)
• $L_1{L}_2$ 是不接触环路的增益乘积之和(不能有公共的节点)
• $L_1{L}_2{L}_3$ 是三个不接触环路的增益乘积之和
• ${\Delta }_k$ 是与第 $k$ 条前向路径不接触的子图的行列式

Note

可以使用DFS的方式来找到所有回路