周期性电流, 电压的有效值

一般情况

I := \frac{1}{T} \int_{0}^{T} i^{2} (t) d t, U := \frac{1}{T} \int_{0}^{T} u^{2} (t) d t

I = \frac{1}{2} I_{m}, U = \frac{1}{2} U_{m}

i = 2 I cos (ω t + ϕ) \to F (t) = 2 I exp (jω t) exp (j ϕ) = 2 \dot{I} exp (jω t)

其中 $\dot{I}$ 为相量, $\dot{I} = I ∠ θ, \dot{U} = U ∠ θ$

u_{1} (t) u_{2} (t) u (t) = 2 U_{1} cos (ω t + Ψ_{1}) = Re (2 \dot{U}_{1} e^{j ω t}) = 2 U_{2} cos (ω t + Ψ_{2}) = Re (2 \dot{U}_{2} e^{j ω t}) = u_{1} (t) + u_{2} (t) = Re (2 \dot{U}_{1} e^{j ω t}) + Re (2 \dot{U}_{2} e^{j ω t}) = Re (2 \dot{U}_{1} e^{j ω t} + 2 \dot{U}_{2} e^{j ω t}) = Re (2 \dot{U} (\dot{U}_{1} + \dot{U}_{2}) e^{j ω t})

对于同频正弦量, $\dot{F} = \dot{F}_{1} + \dot{F}_{2}$

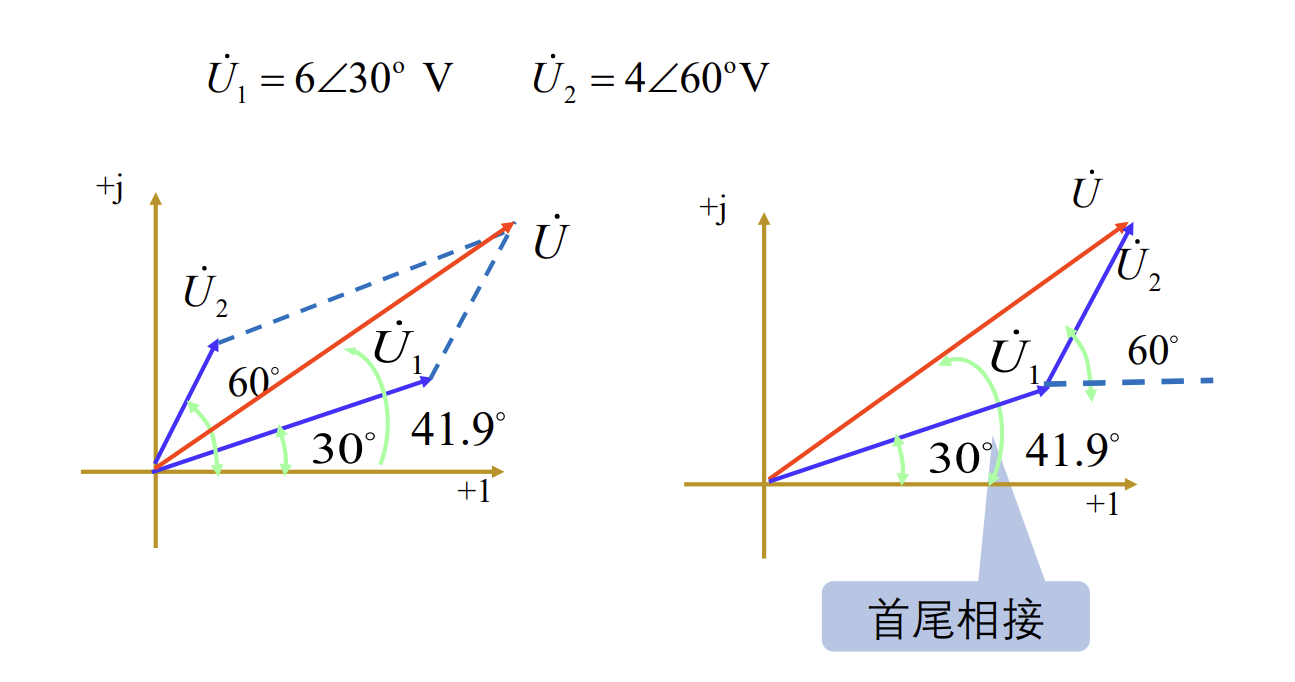
对于非同频的情况, 需要使用相量图

u (t) = R i + L \frac{d i}{d t} + \frac{1}{C} \int_{0}^{t} i (t) d t ⟹ \dot{U} = R \dot{I} + jω L \dot{I} + \frac{I ˙}{jω C}

\dot{U}_{R} = R \dot{I}

\dot{U_{L}} = jω L \dot{I} = j X_{L} \dot{I}

其中

同时 $\dot{U}$ 和 $\dot{I}$ 的相位为 $\frac{π}{2}$ , 从而瞬时功率正负在一个周期内正好相互抵消, 表明电感只储能不耗能

\dot{U}_{C} = \frac{1}{jω C} \dot{I} = - j \frac{1}{ω C} \dot{I} = j X_{C} \dot{I}

其中

对于同频率的情况, $\sum i (t) = 0, \sum u (t) = 0$