Generalized Permutations and Combinations

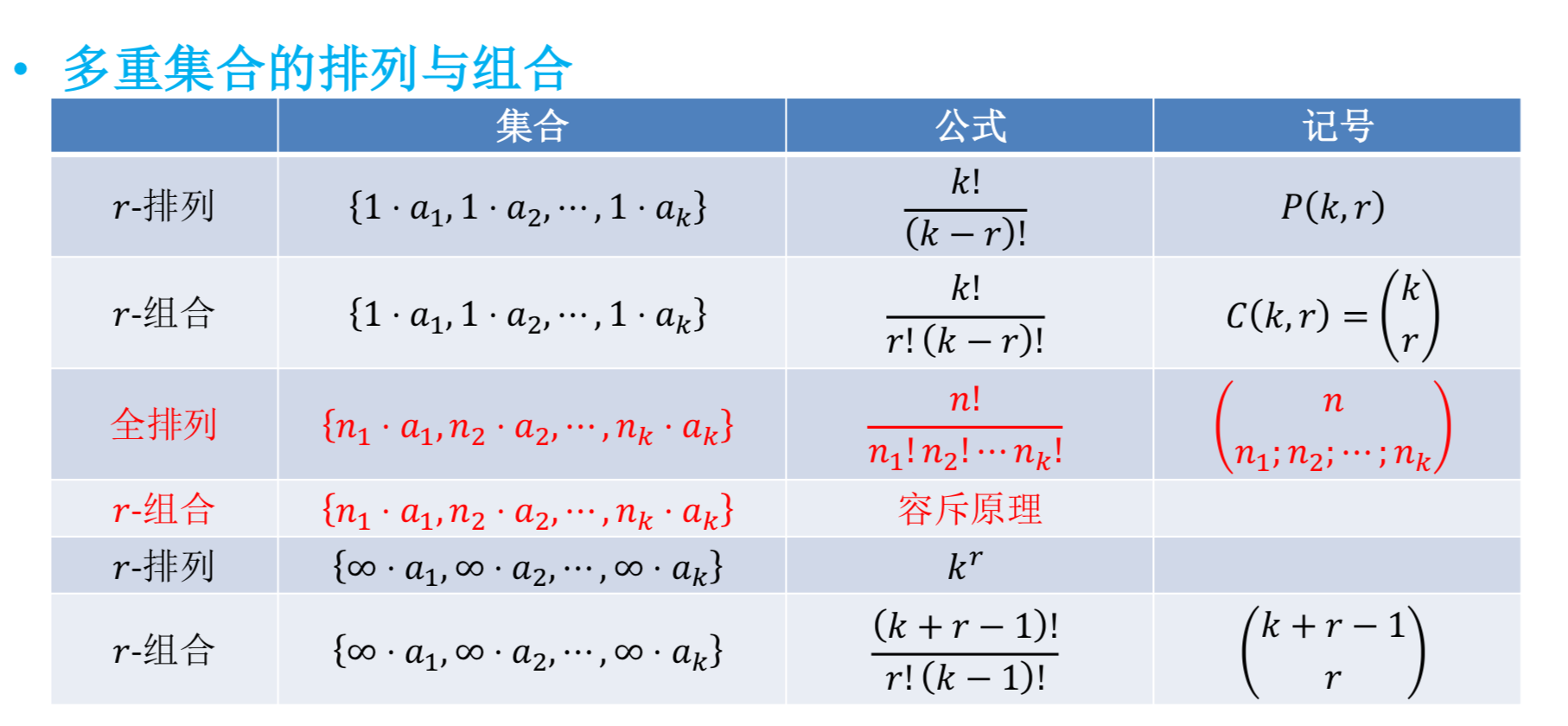
Permutations with Repetition

The number of $r$-permutations of a set of $n$ objects with repetition allowed is $n^r$

Combinations with Repetition

There are $C(n+r-1,r)=C(n+r-1,n-1)$ $r$-combinations from a set with $n$ elements when repetition of elements is allowed.

Each $r$-combination of a set with $n$ elements when repetition is allowed can be represented by a list of $n-1$ bars and $r$ stars. The $n-1$ bars are used to mark off $n$ different cells, with the $i$-th cell containing a star for each time the $i$-th element of the set occurs in the combination. For instance, a $6$-combination of a set with four elements is represented with three bars and six stars. Here

$$\ast \ast |\ast ||\ast \ast \ast$$

represents the combination containing exactly two of the first element, one of the second element, none of the third element and three of the fourth element of the set.

Therefore, the total number of such combinations is $C(n+r-1,r)$

Permutations with Indistinguishable Objects

The number of different permutations of $n$ objects, where there are $n_1$ indistinguishable objects of type $1$, $n_2$ indistinguishable objects of type $2$, ..., and $n_k$ indistinguishable objects of type $k$, is

$$\left(\genfrac{}{}{0ex}{}{n}{n_1{n}_2\cdots n_k}\right)=\frac{n!}{n_1!n_2!\cdots n_k!}$$

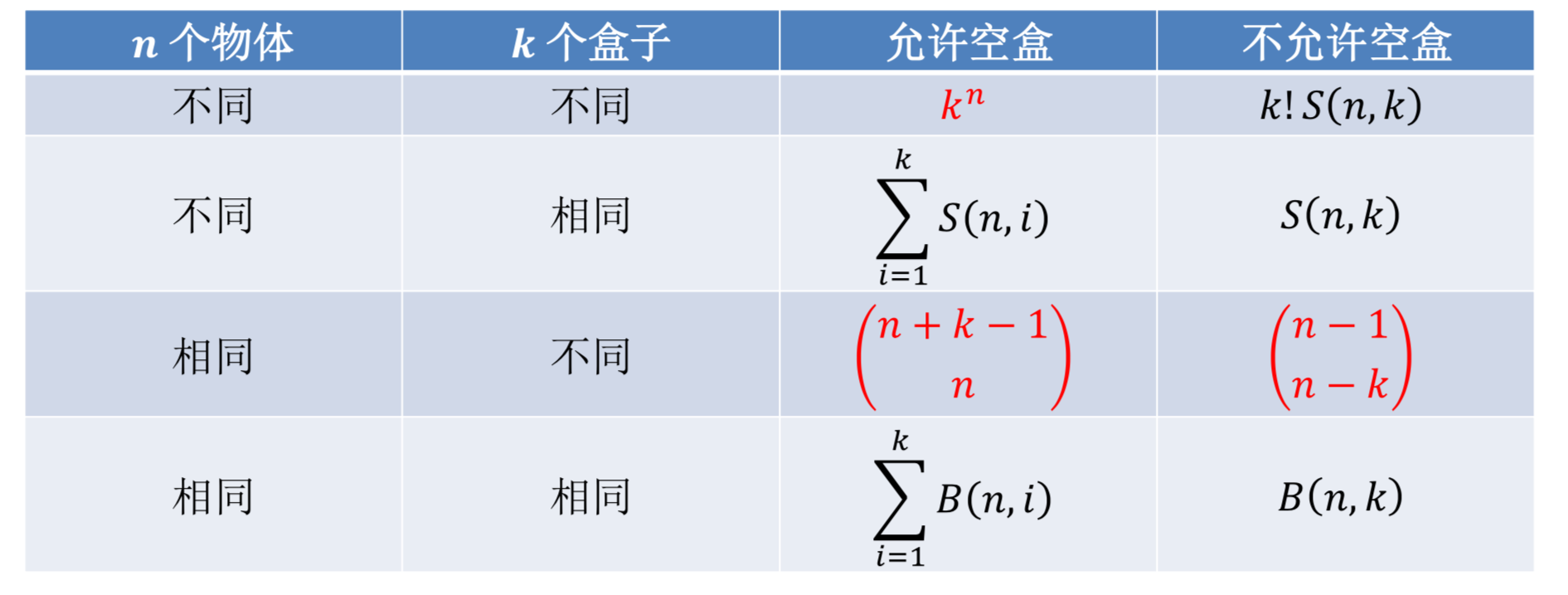
Distributing Objects into Boxes

The number of ways to distribute $n$ distinguishable objects into $k$ distinguishable boxes so that $n_i$ objects are placed into box $i$, $i=1,2,\dots ,k$ equals

$$\left(\genfrac{}{}{0ex}{}{n}{n_1{n}_2\cdots n_k}\right)=\frac{n!}{n_1!n_2!\cdots n_k!}$$