Hypothesis Test

Preliminaries

Hypothesis

 A statistical hypothesis is an assertion about a population parameter that can be tested. There are two main types of hypotheses:  - Null Hypothesis ($H_0$): The default assumption that there is no effect or no difference. For example, it might state that a new drug has no effect on patients.  - Alternative Hypothesis ($H_1$): This represents the opposite of the null hypothesis, suggesting that there is an effect or a difference

Two Types of Error

Fact \ Decision	Accept $H_0$	Reject $H_0$
$H_0$ is true	Good	Type I Error
$H_1$ is true	Type II Error	Good

Significance Level

Significance level, denoted $\alpha$, is the threshold for determining whether to reject the null hypothesis (i.e., the probability for Type I Error to occur). A common choice for $\alpha$ is 0.05, meaning there is a $\alpha$% risk of concluding that a difference exists when there is none.

Rejection Region

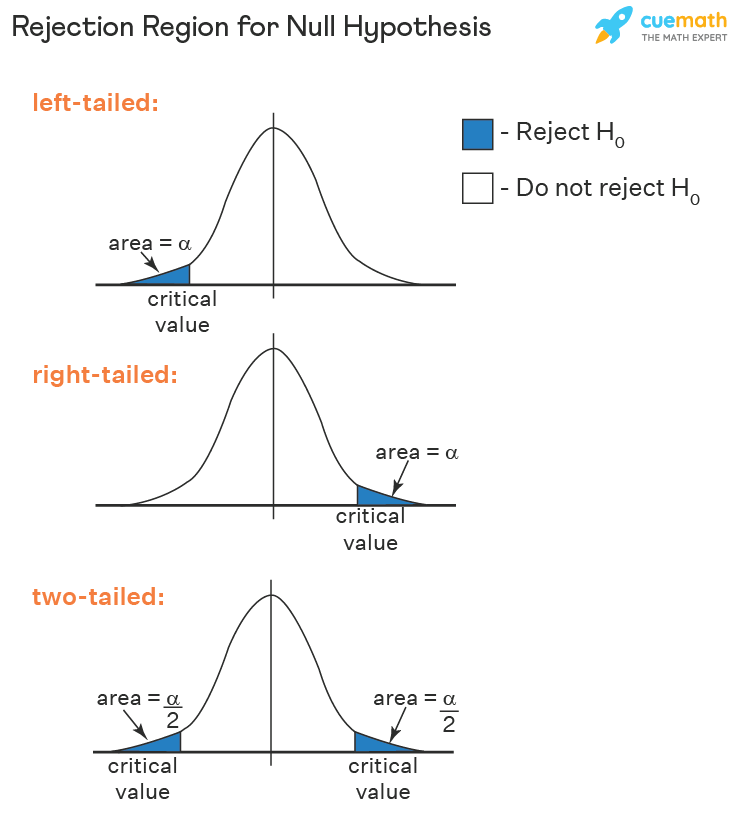
The rejection region (or critical region) is defined as the area on the distribution of the test statistic where, if the calculated statistic falls within this area, you would reject $H_0$​ in favor of the alternative hypothesis ($H_1$).

The critical values are the boundaries that separate the critical region from the acceptance region:

• The chosen significance level ($\alpha$)
• Whether the test is one-tailed or two-tailed.

We say that a rejection region has a size $\alpha$, if it ensures a significance level $\alpha$, i.e. the probability of making a Type I error should be lower than $\alpha$. In the plot of PDF plot, this $\alpha$ is the total area of the critical region, as shown in the figure below

Definition

To generalize the hypothesis testing problem. Let ${\Theta }_0$ and ${\Theta }_1$ be the parameter spaces of $\theta$ when $H_0$ and $H_1$ are true, respectively. The hypothesis testing problem is: $H_0:\theta \in {\Theta }_0⟷H_1:\theta \in {\Theta }_1.$Let $X_1,X_2,\cdots ,X_n$ be a simple random sample, $T$ be the test statistic, $\alpha$ be the significance level, and $W$ be the rejection region. Define the test $\varphi$ as:

$$\varphi =\{\begin{array}{ll}1,& (X_1,X_2,\cdots ,X_n)\in W.\\ 0,& (X_1,X_2,\cdots ,X_n)\notin W.\end{array}$$

Test with Level $\alpha$

If

$$P_{H_0}(\varphi =1)=P_{H_0}\left(\left\{\text{reject}{H}_0\right\}\right)\le \alpha ,\forall \theta \in {\Theta }_0$$

Then we call $\varphi$ a test with level $\alpha$

Power of a Test

The power of a hypothesis test is a critical measure that reflects its ability to correctly reject a false null hypothesis ($H_0$). That is ${\beta }_{\varphi }(\theta )=P(\varphi =1)$, or

$$\beta (\theta )=P(\theta \in W),\text{where}W\text{is the rejection region}$$

When $H_0$ is true, ${\beta }_{\varphi }(\theta )$ is the probability for type I error to occur; When $H_1$ is true, $1-{\beta }_{\varphi }(\theta )$ is the probability for type II error to occur. Therefore, if $H_0$ is true, then we would have ${\beta }_{\varphi }(\theta )\le \alpha$. And when $H_1$ is true, we hope ${\beta }_{\varphi }(\theta )$ to be as big as possible. As a result, when $H_1$ is true, we call ${\beta }_{\varphi }(\theta )$ is the power of test $\varphi$ at $\theta$.

Uniformly Most Powerful Test (UMPT)

A Uniformly Most Powerful (UMP) test is defined as a hypothesis test that maximizes the probability of correctly rejecting the null hypothesis across all possible alternative hypotheses, while maintaining a fixed significance level $\alpha$. This means that for any alternative hypothesis, the UMP test has the greatest statistical power $1-\beta$

$p$-value

For a test $\varphi$ at level $\alpha$, $T$ is the test statistic. After obtaining the sample, let the observed value of $T$ be $t$. If the rejection region of the hypothesis is of the form $W=\{T>c\}$, then the p-value is defined as

$$p\text{-value}=P_{H_0}(T>t).$$

Additionally, for a rejection region of the form $W=\{T<c\}$, the p-value is $P_{H_0}(T<t)$; for a rejection region of the form $W=\{|T|>c\}$, the p-value is $P_{H_0}(|T|>|t|)$. According to the shape of the rejection region, the p-value is the sum of the probabilities of those data that are more extreme (with a smaller probability of occurrence) than the observed data under the assumption that the null hypothesis is true ().

Warning

if $T$ is a discrete random variable, the sum must include the probability of the observed value. That is, use $T\ge t$ instead of $T>t$

In other words, the p-value is the minimum significance level required to reject the null hypothesis based on the observed sample. That is

• If $p>\alpha$, we accept $H_0$
• If $p\le \alpha$, we reject $H_0$

Note

If we can define a clear threshold for the hypothesis to be true, use the rejection region approach; if we can't, use the p-value approach

Common Testing Problems

• Simple Tests: $H_0:\theta ={\theta }_0⟷H_1:\theta ={\theta }_1$
• Two-tailed Tests: $H_0:\theta ={\theta }_0⟷H_1:\theta \ne {\theta }_0$
• One-tailed Tests:
  • $H_0:\theta ={\theta }_0⟷H_1:\theta >{\theta }_0$ or $H_0:\theta \le {\theta }_0⟷H_1:\theta >{\theta }_0$
  • $H_0:\theta ={\theta }_0⟷H_1:\theta <{\theta }_0$ or $H_0:\theta \ge {\theta }_0⟷H_1:\theta <{\theta }_0$

General Steps

Below are the general steps for hypothesis testing, divided into four steps:

1. Set the significance level $\alpha$. Obtain a Point Estimation $\hat{\theta }=\hat{\theta }(X_1,X_2,\cdots ,X_n)$, which is usually the maximum likelihood estimate;
2. Based on $\hat{\theta }$, construct the test statistic $T=T(X_1,X_2,\cdots ,X_n)$ such that when $\theta ={\theta }_0$, the distribution of $T$ is known, such as $\mathcal{N}(0,1)$, ${\chi }_n^2$, $t_n$, $F_{m,n}$, etc., and it is independent of $\theta$;
3. Based on $T$, determine the shape of the rejection region according to the practical meaning of the alternative hypothesis $H_1$. It is an inequality or two inequalities about $T$, containing one or two critical values;
4. Based on the significance level $\alpha$, calculate the rejection region of the test, i.e., determine the critical values of the inequality in step 3. Calculate the value of the test statistic $T$ based on the sample, and then determine whether the sample falls into the rejection region. If it does, reject $H_0$; otherwise, accept $H_0$; Alternatively, calculate the p-value of the test. If the p-value is less than $\alpha$, reject $H_0$; otherwise, accept $H_0$.

Tables

Test Mean with Known Variance

Test	Statistics	Distribution	Rejection Region
$H_0:\mu ={\mu }_0\leftrightarrow H_1:\mu \ne {\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{\sigma }$	$\mathcal{N}(0,1)$	$\left\{\mathrm{abs}(T)>u_{1-\alpha /2}\right\}$
$H_0:\mu ={\mu }_0\leftrightarrow H_1:\mu >{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{\sigma }$	$\mathcal{N}(0,1)$	$\left\{T>u_{1-\alpha }\right\}$
$H_0:\mu ={\mu }_0\leftrightarrow H_1:\mu <{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{\sigma }$	$\mathcal{N}(0,1)$	$\left\{T<u_{\alpha }\right\}$
$H_0:\mu \le {\mu }_0\leftrightarrow H_1:\mu >{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{\sigma }$	$\mathcal{N}(0,1)$	$\left\{T>u_{1-\alpha }\right\}$
$H_0:\mu \ge {\mu }_0\leftrightarrow H_1:\mu <{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{\sigma }$	$\mathcal{N}(0,1)$	$\left\{T<u_{\alpha }\right\}$

Test Mean with Unknown Variance

Test	Statistics	Distribution	Rejection Region
$H_0:\mu ={\mu }_0\leftrightarrow H_1:\mu \ne {\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{S}$	$t_{n-1}$	$\left\{\mathrm{abs}(T)>t_{n-1}(1-\alpha /2)\right\}$
$H_0:\mu ={\mu }_0\leftrightarrow H_1:\mu >{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{S}$	$t_{n-1}$	$\left\{T>t_{n-1}(1-\alpha )\right\}$
$H_0:\mu ={\mu }_0\leftrightarrow H_1:\mu <{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{S}$	$t_{n-1}$	$\left\{T<t_{n-1}(\alpha )\right\}$
$H_0:\mu \le {\mu }_0\leftrightarrow H_1:\mu >{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{S}$	$t_{n-1}$	$\left\{T>t_{n-1}(1-\alpha )\right\}$
$H_0:\mu \ge {\mu }_0\leftrightarrow H_1:\mu <{\mu }_0$	$T=\frac{\sqrt{n}(\bar{X}-{\mu }_0)}{S}$	$t_{n-1}$	$\left\{T<t_{n-1}(\alpha )\right\}$

Test Variance with Known Mean

Test	Statistics	Distribution	Rejection Region
$H_0:{\sigma }^2={\sigma }_0^2\leftrightarrow H_1:{\sigma }^2\ne {\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\mu {)}^2$	${\chi }_n^2$	$\left\{T>{\chi }_n^2(1-\frac{\alpha }{2})\right\}\cup \left\{T<{\chi }_n^2(\frac{\alpha }{2})\right\}$
$H_0:{\sigma }^2={\sigma }_0^2\leftrightarrow H_1:{\sigma }^2>{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\mu {)}^2$	${\chi }_n^2$	$\left\{T>{\chi }_n^2(1-\alpha )\right\}$
$H_0:{\sigma }^2={\sigma }_0^2\leftrightarrow H_1:{\sigma }^2<{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\mu {)}^2$	${\chi }_n^2$	$\left\{T<{\chi }_n^2(\alpha )\right\}$
$H_0:{\sigma }^2\le {\sigma }_0^2\leftrightarrow H_1:{\sigma }^2>{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\mu {)}^2$	${\chi }_n^2$	$\left\{T>{\chi }_n^2(1-\alpha )\right\}$
$H_0:{\sigma }^2\ge {\sigma }_0^2\leftrightarrow H_1:{\sigma }^2<{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\mu {)}^2$	${\chi }_n^2$	$\left\{T<{\chi }_n^2(\alpha )\right\}$

Test Variance with Unknown Mean

Test	Statistics	Distribution	Rejection Region
$H_0:{\sigma }^2={\sigma }_0^2\leftrightarrow H_1:{\sigma }^2\ne {\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$	${\chi }_{n-1}^2$	$\left\{T>{\chi }_{n-1}^2(1-\frac{\alpha }{2})\right\}\cup \left\{T<{\chi }_{n-1}^2(\frac{\alpha }{2})\right\}$
$H_0:{\sigma }^2={\sigma }_0^2\leftrightarrow H_1:{\sigma }^2>{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$	${\chi }_{n-1}^2$	$\left\{T>{\chi }_{n-1}^2(1-\alpha )\right\}$
$H_0:{\sigma }^2={\sigma }_0^2\leftrightarrow H_1:{\sigma }^2<{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$	${\chi }_{n-1}^2$	$\left\{T<{\chi }_{n-1}^2(\alpha )\right\}$
$H_0:{\sigma }^2\le {\sigma }_0^2\leftrightarrow H_1:{\sigma }^2>{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$	${\chi }_{n-1}^2$	$\left\{T>{\chi }_{n-1}^2(1-\alpha )\right\}$
$H_0:{\sigma }^2\ge {\sigma }_0^2\leftrightarrow H_1:{\sigma }^2<{\sigma }_0^2$	$T=\frac{1}{{\sigma }_0^2}{\sum }_{i=1}^n(X_i-\bar{X}{)}^2$	${\chi }_{n-1}^2$	$\left\{T<{\chi }_{n-1}^2(\alpha )\right\}$