Atomic Energy Level Structure and Spectra

电子自旋

轨道磁矩

电子绕着原子核做闭合圆周运动, 相当于一个小电流环, 它等价于一个磁偶极子, 其磁矩为

$$\mathbf{\mu }=IS\mathbf{n}$$

这里$I$为小电流环的电流, 大小为

$$I=\frac{e}{T}=\frac{ev}{2\pi r}$$

注意到$\mathbf{n}$的方向和$\mathbf{r}\times \mathbf{v}$的方向一样, 所以我们可以得到

$$\mathbf{\mu }=\frac{evr}{2}\mathbf{n}=-\frac{e}{2m_{\mathrm{e}}}\mathbf{r}\times m_{\mathrm{e}}\mathbf{v}=-\frac{e}{2m_{\mathrm{e}}}\mathbf{L}$$

这里$\mathbf{L}=\mathbf{r}\times m_{\mathrm{e}}\mathbf{v}$. 其大小$L=\sqrt{l(l+1)}\hslash$ 完全由轨道角动量量子数$l$决定.

我们改写一下磁矩的形式, 把角动量无量纲化, 导出一个磁矩单位的量

$${\mathbf{\mu }}_l=-\frac{e}{2m_{\mathrm{e}}}\mathbf{L}=-\frac{{\mu }_{\mathrm{B}}}{\hslash }\mathbf{L},{\mu }_{\mathrm{B}}\equiv \frac{e\hslash }{2m_{\mathrm{e}}}$$

这里${\mu }_{\mathrm{B}}$是 玻尔磁子

又考虑到角动量的$z$分量为$L_z=m_l\hslash$, 所以轨道磁矩的$z$分量为

$${\mu }_{lz}=-m_l{\mu }_{\mathrm{B}},m_l=0,\pm 1,\pm 2,\dots ,\pm l$$

施恩特-格拉赫 实验

实验目的

• 最初是为了验证玻尔-索末菲量子化模型的假设, 即原子的空间取向是量子化的.
• 但结果却意外地揭示了电子具有内在的角动量, 即自旋, 并证实了自旋量子化的存在.

实验装置

1. 原子束源: 通常使用一个加热的炉子, 将金属 (通常是银) 加热成气态, 然后通过一个狭缝形成一束原子束. 银原子因其外层只有一个电子而成为理想的选择.
2. 非均匀磁场: 这是实验的核心. 一个特殊的磁铁产生一个方向上磁场强度变化很大的磁场 (即非均匀磁场) .
3. 探测器: 在磁场后方放置一个探测屏 (最初是玻璃板) , 用来检测通过磁场的原子束的最终位置.

实验过程:

1. 银原子束通过狭缝射出, 进入非均匀磁场.
2. 如果经典物理成立, 由于原子磁矩的方向是随机的, 通过磁场后, 原子束会受到不同程度的偏转, 在探测屏上形成一条连续的条纹.

磁偶极子具有势能

$$U=-{\mathbf{\mu }}_l\cdot \mathbf{B}$$

受到的梯度力

$$\mathbf{F}=-\nabla U=-\left({\mathbf{e}}_x\frac{\partial U}{\partial x}+{\mathbf{e}}_y\frac{\partial U}{\partial y}+{\mathbf{e}}_z\frac{\partial U}{\partial z}\right)$$

3. 然而, 实验结果显示, 原子束并没有形成连续的条纹, 而是分裂成两个分离的束. 这意味着银原子的磁矩只能取两个特定的方向, 而不是任意方向, 这就是空间量子化的体现.
4. 但是如果只存在磁量子数, 那么原子束应该分裂成级数条, 而不是实验中观察到的偶数条

电子自旋

为了解释施恩特-格拉赫实验的结果, 乌仑贝克 (G.E.Uhlenbeck) 和古兹密特 (S.A.Goudsmit) 提出了电子自旋的假设, 他们任务电子具有不变的, 确定的自旋角动量, 自旋是电子的固有属性. 根据已有的实验结果, 他们给出电子的自旋角动量及其$z$方向的分量为

$$\begin{array}{rl}{\mathbf{S}}^2& =s(s+1){\hslash }^2,s=1/2\\ {\mathbf{S}}_z& =m_s\hslash ,m_s=1/2,-1/2\end{array}$$

由此给出电子的自旋磁矩是

$$\{\begin{array}{l}{\mathbf{\mu }}_s=-\frac{g_s{\mu }_B}{\hslash }\mathbf{S}\\ {\mu }_{sz}=-m_s{g}_s{\mu }_B\end{array}$$

这里 $g_s$ 称为电子的自旋 $g$ 因子, 它的取值为 $g_s=2$. 这个因子的引入完全是为了解释实验结果. 为了形式上的统一, 我们也可以把轨道磁矩写成类似的形式

$$\{\begin{array}{l}{\mathbf{\mu }}_l=-\frac{g_l{\mu }_B}{\hslash }\mathbf{L}\\ {\mu }_{lz}=-m_l{g}_l{\mu }_B\end{array}$$

这里 $g_l$ 称为电子的轨道 $g$ 因子, 只不过 $g_l=1$

泡利不相容原理

全同粒子

全同粒子是这样一类粒子, 它们的内禀属性(例如禁止质量, 电荷, 自旋, 磁矩等不受外界作用影响的属性) 完全相同, 且所在的物理环境一样. 例如氦原子中的两个电子, 它们的内禀属性相同. 当He原子处于1s2p的状态时, 只能说一个电子处于1s状态, 另一个电子出于2p状态. 具体到是哪一个电子处于1s, 哪一个电子处于2p, 我们并不知道, 也无法知道. 但是我们总是要描述He原子的这一状态, 我们在忽略电子-电子之间的相互作用且不考虑自旋的时候, He的$1s2{\mathrm{p}}_0$ ($0$ 表示 $m_l=0$) 状态的波函数可以写为

$${\psi }_{\mathrm{I}}({\mathbf{r}}_1,{\mathbf{r}}_2)={\psi }_{1s}({\mathbf{r}}_1){\psi }_{2{\mathrm{p}}_0}({\mathbf{r}}_2)$$

如果我们交换这两个电子的状态, 我们应该得到同样一个He原子

$${\psi }_{\mathrm{II}}({\mathbf{r}}_1,{\mathbf{r}}_2)={\psi }_{1s}({\mathbf{r}}_2){\psi }_{2{\mathrm{p}}_0}({\mathbf{r}}_1)$$

因此, 全通性原理对波函数加了一个约束, 也就是波函数的交换对称性

波函数的交换对称性

对于两个全同粒子组成的系统, 其波函数可表示为

$$\psi (q_1,q_2)$$

这里 $q_1$ 和 $q_2$ 分别是粒子 $1$ 和粒子 $2$ 的坐标, 既包含空间坐标也包含自旋坐标, 为了说明波函数的交换对称性, 我们引入交换算符 ${\hat{p}}_{12}$, 有

$${\hat{p}}_{1,2}\psi (q_1,q_2)=\psi (q_2,q_1)$$

根据全同性原理, 交换两个粒子并不改变体系的物理状态, 因此交换前后的波函数只能相差一常数 $\lambda$

$${\hat{p}}_{12}\psi (q_1,q_2)=\lambda \psi (q_1,q_2)$$

把粒子交换量子, 有

$${\hat{p}}_{1,2}\psi (q_1,q_2)={\lambda }^2\psi (q_1,q_2)A=\psi (q_1,q_2)⟹\lambda =\pm 1$$

也就是对应交换算符的本征值. 如果 $\lambda =1$ , 我们称这个波函数是交换对称的; 如果 $\lambda =-1$, 我们称这个波函数是交换反对称的

泡利不相容原理

在多电子原子中, 任何两个电子都不能处于完全相同的状态. 也就是说, 任意两个电子的 $4$ 个量子数 ($n,l,m_l,m_s$) 不能完全相同.

泡利不相容原理对电子系统波函数的交换对称性提出了明确的限制, 也即多电子系统的波函数必须满足交换反对称性的要求.

多粒子体系波函数的交换对称性是由粒子本身的内禀属性决定的

• 自旋角动量为 $\hslash /2$ 的奇数倍的粒子是费米子, 它的波函数是交换反对称的, 如电子, 质子和中子
• 自旋角动量为 $\hslash$ 的整数倍的粒子是玻色子, 它的波函数是交换对称的, 如光子, 氢原子

由奇数个费米子组成的复合粒子是是费米子, 由偶数个费米子组成的复合粒子是玻色子

交换效应

费米子的交换反对称性

电子是费米子, 要求其总波函数在交换任意两个电子时必须改变符号 (反对称) . 对于He原子的两个电子系统, 反对称波函数可以写成:

$${\psi }_A(q_1,q_2)=\frac{1}{\sqrt{2}}[{\psi }_a(q_1){\psi }_{\beta }(q_2)-{\psi }_{\beta }(q_1){\psi }_a(q_2)]$$

波函数的分离

在近似下, 总波函数可以分离为空间部分和自旋部分的乘积:

$${\psi }_A(q_1,q_2)=\psi ({\mathbf{r}}_1,{\mathbf{r}}_2)\chi$$

自旋波函数

单电子自旋状态

• 自旋向上: $m_s=1/2$ ( ${\sigma }^{+}$ 或↑)
• 自旋向下: $m_s=-1/2$ ( ${\sigma }^{-}$ 或↓)

两电子自旋组合

四种可能的乘积组合中, 可以构造出:

• 三重态 (对称, 称之为 $S=1$ ) : ${\chi }_{11}={\sigma }^{+}(1){\sigma }^{+}(2)$ ${\chi }_{10}=\frac{1}{\sqrt{2}}[{\sigma }^{+}(1){\sigma }^{-}(2)+{\sigma }^{-}(1){\sigma }^{+}(2)]$ ${\chi }_{1-1}={\sigma }^{-}(1){\sigma }^{-}(2)$
• 单态 (反对称, 称之为 $S=0$ ) : ${\chi }_{00}=\frac{1}{\sqrt{2}}[{\sigma }^{+}(1){\sigma }^{-}(2)-{\sigma }^{-}(1){\sigma }^{+}(2)]$

总波函数的构造

根据反对称要求, 总波函数只能有如下两种构造形式

• 对称空间波函数 × 反对称自旋波函数
• 反对称空间波函数 × 对称自旋波函数

交换效应

当两个电子靠近时( ${\mathbf{r}}_1\approx {\mathbf{r}}_2$ ):

• 对于反对称空间波函数 (匹配对称自旋波函数, 即S=1三重态) : ${\psi }_A\approx 0$ → 电子互相"避开" → 库仑排斥减小 → 能量降低
• 对于对称空间波函数 (匹配反对称自旋波函数, 即S=0单态) : ${\psi }_S\approx \sqrt{2}{\psi }_{\alpha }({\mathbf{r}}_1){\psi }_{\beta }({\mathbf{r}}_2)$ → 电子靠近概率增加 → 库仑排斥增大 → 能量升高

物理意义

交换效应不是真实的物理相互作用, 而是由于波函数对称性要求导致的量子力学效应:

• 自旋平行的电子 (三重态) 会"避免"在空间同一位置出现
• 自旋反平行的电子 (单态) 会在空间更靠近

总结

1. 交换效应源于费米子波函数的反对称要求
2. 它导致自旋平行和反平行的电子有不同的空间分布
3. 这种分布差异影响了电子间的库仑相互作用能
4. 结果是自旋平行的状态能量更低 (在He的1s2s组态中)

元素周期表的排列

量子数亏损

在单电子氢原子中, 电子能级仅由主量子数 $n$ 决定, 能量公式为:

$$E_n=-\frac{13.6\text{eV}}{n^2}$$

但在多电子原子中, 由于电子间的库仑排斥和轨道贯穿效应 (内层电子屏蔽核电荷) , 外层电子的有效核电荷 $Z^{\ast }$ 减小, 且能级不仅依赖 $n$ , 还与轨道角动量量子数 $l$ 相关. 此时, 能量可修正为:

$$E_{nl}=-\frac{13.6\text{eV}}{(n-{\Delta }_l{)}^2}$$

其中 ${\Delta }_l$ 即为 量子数亏损, 表征实际能级与氢原子能级的偏离程度.

理论解释

量子数亏损的根源在于:

• 轨道贯穿效应: 低 $l$ 电子 (如s电子) 的波函数在核附近有较大概率分布, 感受到更强的有效核电荷 $Z^{\ast }$ , 导致能量显著降低 ( ${\Delta }_l$ 较大) .
• 屏蔽效应: 高 $l$ 电子 (如d、f电子) 的轨道较 "松散" , 被内层电子屏蔽更多, $Z^{\ast }$ 接近1, ${\Delta }_l$ 较小 (接近氢原子能级) .

例如, 碱金属的价电子能级中:

• ${\Delta }_s>{\Delta }_p>{\Delta }_d\approx 0$ , 反映s电子贯穿能力最强, 能级下移最明显.

量子数亏损通常通过里德伯公式描述:

$$E_{nl}=-\frac{13.6\text{eV}}{(n-{\delta }_l{)}^2},{\delta }_l={\Delta }_l+\text{高阶修正}$$

其中 ${\delta }_l$ 可通过光谱实验数据拟合得到. 例如, 钠原子的3s能级( $n=3$ )的 ${\Delta }_s\approx 1.37$ , 而3p的 ${\Delta }_p\approx 0.88$ .

应用与意义

• 解释能级交错: 如4s能级低于3d (图3.3.2) , 因s电子的 ${\Delta }_l$ 更大, 导致有效主量子数 $n^{\ast }=n-{\Delta }_l$ 更小, 能量更低.
• 元素周期表结构: 量子数亏损决定了电子填充顺序 (如先填4s后3d) , 直接关联周期表中过渡金属的排列 (表3.3.2) .
• 光谱分析: 用于精确计算碱金属和稀土元素的光谱线位置.

自旋 - 轨道相互作用

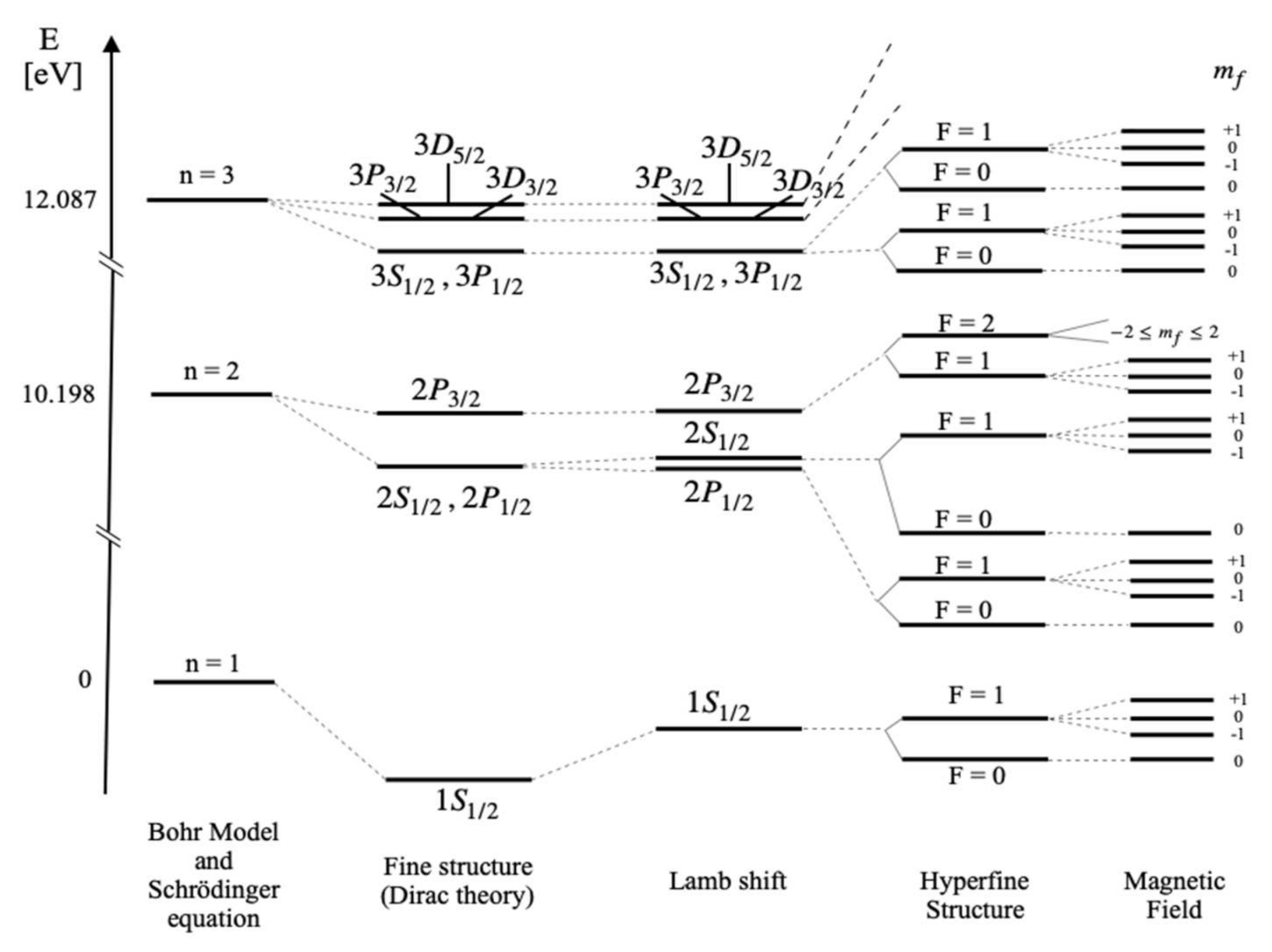
在之前的所有讨论中, 我们都忽略了各种磁相互作用对原子能级结构的影响, 例如自旋磁矩和轨道磁矩之间的相互作用, 原子核磁矩和电子磁矩之间的相互作用等. 由于磁相互作用要比电相互作用弱很多, 所以它对原子能级结构的影响要小得多; 往往造成原子能级结构的细小分裂或者移动, 这些细小的分裂和移动称为原子的精细和超精细结构.

自旋 - 轨道相互作用

一般而言, 我们说电子绕着原子实运动, 这里把原子实当作是静止的. 但是我们也可换一个角度, 认为电子是静止的, 而原子实在绕着电子做运动. 此时, 原子实运动在电子处产生的磁场可由经典电磁学给出

$$\mathbf{B}=-\frac{1}{4\pi {\epsilon }_0}\frac{Z^{\ast }e\mathbf{v}\times \mathbf{r}}{c^2{r}^3}$$

由于轨道角动量 $\mathbf{L}=\mathbf{r}\times m\mathbf{v}$ 是守恒的, 所以我们有

$$\mathbf{B}=\frac{1}{4\pi {\epsilon }_0}\frac{Z^{\ast }e\mathbf{L}}{m_e{c}^2{r}^3}$$

自旋磁矩与轨道运动产生的磁场发生相互作用, 其势能为

$$U^{\prime }=-{\mathbf{\mu }}_s\cdot \mathbf{B}=\frac{g_S{\mu }_{\mathrm{B}}{Z}^{\ast }e}{4\pi {\epsilon }_0{m}_{\mathrm{e}}{c}^2\hslash }\frac{1}{r^3}\mathbf{S}\cdot \mathbf{L}=\frac{Z^{\ast }{e}^2}{4\pi {\epsilon }_0{m}_{\mathrm{e}}^2{c}^2}\frac{1}{r^3}\mathbf{S}\cdot \mathbf{L}$$

实际上, 我们感兴趣的还是在原子实静止坐标系中的能量. 考虑到相对论效应, 上面的 $\mathbf{B}$ 和 $U^{\prime }$ 会多出来一个1/2的因子. 因此, 真实的势能为

$$U=\frac{1}{2}\frac{Z^{\ast }{e}^2}{4\pi {\epsilon }_0{m}_{\mathrm{c}}^2{c}^2}\frac{1}{r^3}\mathbf{S}\cdot \mathbf{L}$$

上式所示的势能来自于自旋-轨道之间的磁相互作用. 称为自旋-轨道相互作用. 考虑自旋-轨道相互作用之后, 原子的能级结构必定会有所调整.

总角动量

如果不考虑自旋-轨道相互作用, 则轨道角动量和自旋角动量是互相独立的, 它们都是守恒量. 相应地, $L^2,L_z,S^2,S_z$ 都有确定的值. 相应地, 与这些角动量对应的量子数 $l,m_l,s$ 和 $m_s$ 叫作好量子数 (good quantum number) . 但是自旋-轨道相互作用总是存在的, 自旋磁矩肯定会感受到轨道运动产生的磁场. 我们首先来讨论一下磁矩在磁场中的运动. 由经典电磁学的知识可知, 一个磁矩在磁场中会感受到一个力矩. 具体到自旋磁矩, 它感受到的力矩 $\mathbf{\tau }$ 为

$$\mathbf{\tau }={\mathbf{\mu }}_s\times \mathbf{B}$$

这里 $\mathbf{B}$ 为电子轨道运动产生的磁场.

由经典力学可知, 力矩等于角动量的变化率:

$$\frac{\mathrm{d}\mathbf{S}}{\mathrm{d}t}=\mathbf{\tau }={\mathbf{\mu }}_{\mathbf{s}}\times \mathbf{B}$$

这里已经考虑了相对论变化引进的因子 , , 上式可简化为

$$\frac{\mathrm{d}\mathbf{S}}{\mathrm{d}t}=\xi (\mathbf{r})\mathbf{L}\times \mathbf{S}$$

这表明自旋角动量 $\mathbf{S}$ 在绕轨道角动量 $\mathbf{L}$ (也即内磁场方向)做进动, 进动的角频率为

$$\omega =\xi (r)L$$

由于原子没有与外界发生相互作用, 这里所示的力矩是一个内力矩. 也即轨道运动产生的磁场使得自旋磁矩感受到力矩 $\mathbf{\tau }$ , 反过来, 轨道磁矩也受到一个反力矩一 $\mathbf{\tau }$ , 它是由自旋磁矩产生的磁场与轨道磁矩相耦合而产生的:

$$\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}=-\mathbf{\tau }=\xi (\mathbf{r})\mathbf{S}\times \mathbf{L}$$

考虑到自旋-轨道相互作用后, 轨道角动量 $\mathbf{L}$ 和自旋角动量 $\mathbf{S}$ 对时间的偏导不为零, 也即它们都不再具有确定的值, 也不再是守恒量了.这也告诉我们, $\mathbf{L}$ 绕 $\mathbf{S}$ 进动的同时, $\mathbf{S}$ 也在绕 $\mathbf{L}$ 进动,且二者进动的角频率并不相等, 相互耦合的方式十分复杂. 为此,我们引人一个新的角动量 $\mathbf{J}$ "

$$\mathbf{J}=\mathbf{L}+\mathbf{S}$$

有

$$\frac{\mathrm{d}\mathbf{J}}{\mathrm{d}t}=\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}+\frac{\mathrm{d}\mathbf{S}}{\mathrm{d}t}=\xi (\mathbf{r})[\mathbf{L}\times \mathbf{S}+\mathbf{S}\times \mathbf{L}]=0$$

因此, $\mathbf{J}$ 是一个守恒量, 它是轨道角动量和自旋角动量的矢量和,我们称之为原子的 总角动量 (total angular momentum) . 有了总角动量,我们再来考察轨道角动量和自旋角动量, 有

$$\{\begin{array}{l}\frac{\mathrm{d}\mathbf{L}}{\mathrm{d}t}=\xi (\mathbf{r})\mathbf{J}\times \mathbf{L}\\ \frac{\mathrm{d}\mathbf{S}}{\mathrm{d}t}=\xi (\mathbf{r})\mathbf{J}\times \mathbf{S}\end{array}$$

这表明, $\mathbf{L}$ 和 $\mathbf{S}$ 同时绕着 $\mathbf{J}$ 以相同的角频率 $\xi (r)J$ 在做进动, 如图3.4.3所示, 是一个相当简洁的物理图像了.

因此, 考虑到自旋-轨道相互作用后, 轨道角动量和自旋角动量的大小仍不变, 也即 ${\mathbf{L}}^2$ 和 ${\mathbf{S}}^2$ 不变, 还是守恒量. 但它们不再具有确定的方向, 也即 $L_z$ 和 $S_z$ 不再是守恒量了. 原子的总角动量是新的守恒量, 它具有确定的大小和方向, 也即 ${\mathbf{J}}^2$ 和 ${\mathbf{J}}_z$ 都是新的不变量.

设总角动量量子数为 $j$ , 则有

$${\mathbf{J}}^2=j(j+1){\hslash }^2$$

此时 $J_z$ 对应的磁量子数 $J_z=m_j\hslash$, 这里 $m_j$ 可以取 $j,j-1,\dots ,-j+1,-j$. 且有

$$m_j=m_l+m_s$$

对于 H 原子的 2p 轨道, 我们有

$$\begin{array}{rl}{m}_l& =1,0,-1\\ m_s& =-\frac{1}{2},\frac{1}{2}\end{array}$$

所以对应的 $m_j$ 的值有 $6$ 个. 给 $m_j$ 取绝对值可以由 $m_j$ 得出 $j$ 的值

考虑到自旋-轨道相互作用后, 原子的守恒量变为 $L^2,S^2,J^2$ 和 $J_z$, 也就是好量子数为 $n,l,s,j$ 和 $m_j$. 无外磁场时, 体系的能量对 $m_j$ 简并, 由 $n,l,s$ 和 $j$ 决定. 由此可以引入原子态符号(也叫谱项)

$${}^{2S+1}{L}_J$$

来表示原子的能量状态. 当 $L=0,1,2,\dots ,$ 时, 用大写的 S, P, E, ... 表示.而 $2S+1$ 用数字写于 $L$ 的左上角, 它也称为 多重态 , 其数值往往等于能级分裂的个数

例子: 对于H原子来说

• 1s 轨道, 它的 $l=0$ 且 $S=\frac{1}{2}$ ($S=\frac{1}{2}\times N_e$, 这里 $N_e$ 为 轨道 上电子的个数) , 所以我们有 $j=\left|l\pm S\right|=\frac{1}{2}$, 从而原子态符号为 ${}^2{\mathrm{S}}_{1/2}$
• 2p 轨道, 它的 $l=1$ 且 $S=\frac{1}{2}$, 所以 $j=\left|l\pm S\right|=\frac{1}{2},\frac{3}{2}$, 于是原子态符号为 ${}^2{\mathrm{P}}_{1/2,3/2}$.
• 3d, 4f 轨道同理有 ${}^2{\mathrm{D}}_{3/2,5/2}$ ${}^2{\mathrm{F}}_{5/2,7/2}$ 可以看到, 除了 1s 轨道因为 $l=0$ 没有轨道角动量能级没有分裂外, 2p, 3d, 4f 这些能级都分裂成了两条

单电子原子的能级结构和光谱

碱金属的能级结构和光谱

氢原子能级的精细结构和精密光谱

兰姆位移

考试: 兰姆位移的实验装置 卢瑟福 JJ汤姆逊 康普顿 弗兰克-赫兹实验

原子核自旋导致的超精细结构

$LS$ 耦合 和 $jj$ 耦合

之前我们使用中心势近似来处理多电子原子的能级结构问题, 指出多电子原子的能级主要由电子组态决定, 并忽略了较弱的剩余静电势和各种磁相互作用的影响. 但是, 对于多电子原子, 剩余静电势或自旋-轨道相互作用与中心势相比并不是一个非常小的量, 因此仅采用中心势近似是不够的.

根据这两种剩余相互作用的相对强弱, 我们有两种近似的处理方法 (耦合方式)

$LS$ 耦合

当剩余静电势远大于自旋-轨道相互作用时, 原子角动量的耦合形式对应于 $LS$ 耦合. 也就是先考虑剩余静电势, 再考虑自旋-轨道相互作用 (比如说对于两个电子的体系 $L_1,S_1,L_2,S_2$, 先耦合 $L_1,L_2\to L$ 和 $S_1,S_2\to S$, 再耦合 $L,S$).

适用于原子基态和轻原子低激发态

剩余静电势的耦合

对于多个价电子, 电子间的剩余静电势 (非中心力) 会使每个电子都受到一个力矩. 但是, 所有这些内力矩的总和为零. (注意: 这里主要考虑价电子, 因为满壳层或满支壳层的电子云是球对称的, 其贡献可以看作是对中心场的修正, 不产生净的非中心效应) .

由于每个电子受到非零力矩 ${\vec{\tau }}_i$ , 根据角动量定理 $\mathrm{d}{\vec{l}}_i/\mathrm{d}t={\vec{\tau }}_i$ , 单个电子的轨道角动量 ${\vec{l}}_i$ 不守恒了 (方向会变) . 同理, 虽然剩余静电势不直接作用于自旋, 但通过泡利原理和波函数对称性要求, 它间接影响自旋状态的组合, 导致单个电子的自旋角动量 ${\vec{s}}_i$ 的投影 $m_{s_i}$ 也不再是好量子数.

但是, 由于总内力矩 $\sum {\vec{\tau }}_i=0$ , 所以总轨道角动量 $\vec{L}=\sum {\vec{l}}_i$ 是守恒的 ( $\mathrm{d}\vec{L}/\mathrm{d}t=\sum {\vec{\tau }}_i=0$ ).

类似地, 剩余静电相互作用不直接依赖于自旋, 它不产生改变总自旋的力矩, 所以总自旋角动量 $\vec{S}=\sum {\vec{s}}_i$ 也是守恒的 ( $\mathrm{d}\vec{S}/\mathrm{d}t=0$ ).

在强大的剩余静电势作用下, 我们可以想象每个 ${\vec{l}}_i$ 都在围绕着它们的矢量和 $\vec{L}$ 快速进动 (旋转) , 而每个 ${\vec{s}}_i$ 都在围绕着它们的矢量和 $\vec{S}$ 快速进动. $\vec{L}$ 和 $\vec{S}$ 本身的方向和大小在只考虑剩余静电势时是恒定的. 这就像陀螺各自绕着一个固定的轴旋转.

自旋-轨道相互作用

现在,我们把之前忽略的, 较弱的自旋-轨道相互作用加进来. 这个相互作用可以看作是总轨道磁矩 (与 $\vec{L}$ 相关) 和总自旋磁矩 (与 $\vec{S}$ 相关) 之间的相互作用.

这个相互作用会对 $\vec{L}$ 和 $\vec{S}$ 产生力矩, 但这个力矩是内力矩, 它使得 $\vec{L}$ 和 $\vec{S}$ 都不再独立守恒 (它们的方向开始变化) . 但是, 这个内部相互作用不会改变原子总角动量 $\vec{J}=\vec{L}+\vec{S}$ . 因此, $\vec{J}$ 是守恒的 ( $\mathrm{d}\vec{J}/\mathrm{d}t=0$ ). 之前 "固定" 的 $\vec{L}$ 和 $\vec{S}$ 现在开始相互作用. 想象 $\vec{L}$ 和 $\vec{S}$ 作为一个整体, 围绕着它们的矢量和 $\vec{J}$ 进行较慢的进动. 因为自旋-轨道相互作用比剩余静电势弱, 所以这个 $(\vec{L},\vec{S})$ 绕 $\vec{J}$ 的进动频率远低于 ${\vec{l}}_i$ 绕 $\vec{L}$ 和 ${\vec{s}}_i$ 绕 $\vec{S}$ 的进动频率.

总结LS耦合图像: 快速的 $({\vec{l}}_i\to \vec{L})$ 和 $({\vec{s}}_i\to \vec{S})$ 耦合, 然后是慢速的 $(\vec{L},\vec{S}\to \vec{J})$ 耦合.

例子: 2p3d电子的LS耦合过程如下:

1. 确定单电子的角动量:
   • 对于2p电子, 轨道角动量 $l_1=1$ , 自旋角动量 $s_1=\frac{1}{2}$ .
   • 对于3d电子, 轨道角动量 $l_2=2$ , 自旋角动量 $s_2=\frac{1}{2}$ .
2. 耦合轨道角动量:
   • 总轨道角动量 $L=|l_1-l_2|,|l_1-l_2|+1,...,l_1+l_2$ .
   • 因此, $L=|1-2|,|1-2|+1,1+2=1,2,3$ , 对应于 P, D, F 态.
3. 耦合自旋角动量:
   • 总自旋角动量 $S=|s_1-s_2|,|s_1-s_2|+1,...,s_1+s_2$ .
   • 因此, $S=|\frac{1}{2}-\frac{1}{2}|,\frac{1}{2}+\frac{1}{2}=0,1$ , 对应于单重态和三重态.
4. 耦合总角动量:
   • 总角动量 $J=|L-S|,|L-S|+1,...,L+S$ .
   • 对于每个 $L$ 和 $S$ 的组合, 计算可能的 $J$ 值. 现在, 我们将所有可能的组合列出, 并给出相应的原子态符号 ${}^{2S+1}{L}_J$ :

• $L=1$ (P), $S=0$ : $J=1$ , 态符号: ${}^1{P}_1$
• $L=1$ (P), $S=1$ : $J=0,1,2$ , 态符号: ${}^3{P}_0$ , ${}^3{P}_1$ , ${}^3{P}_2$
• $L=2$ (D), $S=0$ : $J=2$ , 态符号: ${}^1{D}_2$
• $L=2$ (D), $S=1$ : $J=1,2,3$ , 态符号: ${}^3{D}_1$ , ${}^3{D}_2$ , ${}^3{D}_3$
• $L=3$ (F), $S=0$ : $J=3$ , 态符号: ${}^1{F}_3$
• $L=3$ (F), $S=1$ : $J=2,3,4$ , 态符号: ${}^3{F}_2$ , ${}^3{F}_3$ , ${}^3{F}_4$ 因此, 2p3d电子的LS耦合产生的原子态符号为: ${}^1{P}_1$ , ${}^3{P}_0$ , ${}^3{P}_1$ , ${}^3{P}_2$ , ${}^1{D}_2$ , ${}^3{D}_1$ , ${}^3{D}_2$ , ${}^3{D}_3$ , ${}^1{F}_3$ , ${}^3{F}_2$ , ${}^3{F}_3$ , ${}^3{F}_4$ .

非同科与同科电子 (多电子体系)

• 非同科 (Un-equivalent): 电子的 $(n,l)$ 不全相同. 耦合时直接用角动量加法规则计算可能的 $L$ 和 $S$ 值.
• 同科 (Equivalent): 电子的 $(n,l)$ 相同. 需要考虑泡利不相容原理, 它限制了可能的 $(L,S)$ 组合. 例如, 对于两个同科电子, 要求 $(-1{)}^{L+S}=1$ (即 $L+S$ 为偶数) , 因为总波函数 (空间部分 × 自旋部分) 必须是反对称的.

朗德间隔定则

在一个多重态 (固定的 $L$, $S$) 内部, 由自旋-轨道作用引起相邻两个精细结构能级 ( $J$ 和 $J+1$ ) 的能量间隔 $\Delta E=E_{J+1}-E_J$ 正比于较大的那个 $J$ 值, 即 $(J+1)$ . 这是因为自旋-轨道相互作用对能级的修正量 $U_{SO}^{\prime }\propto [J(J+1)-L(L+1)-S(S+1)]$ . 计算 $E_{J+1}-E_J$ 得到 $\propto (J+1)$ .

该定则定量描述了在 LS 耦合下, 弱自旋-轨道作用如何根据总角动量 $J$ 的不同值来分裂能级. 间隔有规律, 可以用来验证原子谱是否符合 LS 耦合.

洪特规则

经验规则, 用来判断给定电子组态下能量最低的原子态.

• 规则1 (最大 $S$): 能量最低的态具有最大可能的总自旋量子数 $S$. $S$ 最大时, 自旋倾向于平行排列 (自旋波函数对称) . 根据泡利原理, 空间波函数必须反对称. 反对称的空间波函数意味着电子倾向于互相避开, 减小了库仑排斥能, 从而降低总能量. 这与 "交换能" 有关.
• 规则2 (最大 $L$, 对于给定最大 $S$): 在 $S$ 相同的态中, $L$ 最大的态能量最低. $L$ 最大时, 可以想象电子倾向于以同方向绕核运动 . 这样它们 "擦肩而过" 的机会更少, 相互距离较远, 同样减小了库仑排斥能.
• 规则3 (最小/最大 $J$): 对于同科电子 $(nl{)}^{\nu }$ 构成的多重态 (固定 $L$, $S$) :
  • 正常次序 (Normal order): 如果壳层填充数 $\nu \le 2l+1$ (未满半满), 则 J 最小的能级能量最低.
  • 倒转次序 (Inverted order): 如果壳层填充数 $\nu >2l+1$ (超过半满), 则 J 最大的能级能量最低. 这与自旋-轨道耦合能 $U_{SO}^{\prime }\propto \xi (L,S)[\dots ]$ 中的耦合系数 $\xi (L,S)$ 的符号有关. 对于未满半满的壳层, $\xi$ 通常为正, 导致 J 小的能量低. 对于超过半满的壳层, 可以看作是 "空穴" 的耦合, 其有效 $\xi$ 为负, 导致 $J$ 大的能量低.

Note

确定原子的基态需要结合电子排布规则 (如能量最低原理, 泡利原理, 洪特定则) . 先确定电子组态, 然后对未满壳层的价电子应用洪特定则找到能量最低的 ${}^{2S+1}{L}_J$ 态.

例子

我们来用洪特规则确定铁 (Fe) 的基态电子排布. 铁的原子序数是26, 因此它有26个电子. 其电子排布式为 $1s^{2}2s^{2}2p^{6}3s^{2}3p^{6}4s^{2}3d^6$ . 我们需要重点关注未充满的 $3d$ 轨道.

• 最大 $S$ 规则: 6个d电子中, 5个电子先占据不同轨道且自旋平行 ( $m_l=-2,-1,0,+1,+2$ ) , 第6个电子与其中一个自旋配对. 因此总自旋 $S=(5\times \frac{1}{2})-\frac{1}{2}=2$ (自旋多重度 $2S+1=5$ ) .
• 最大 $L$ 规则: 对剩余未配对电子, 计算总轨道角动量最大值. 由于大家都在 3d 上, 所以我们只需要考虑角动量的 $z$ 轴分量. 每个平行自旋电子占据所有 $m_l$ 轨道, 其总代数和为 $0$. 第6个电子只能重复占据某一轨道 (最大的就是 $m_l=+2$ ) , 此时 $L=|0+2|=2$ (D) .
• $J$ 的选择: 由于 $3d^6$ 填充数 $\nu =6>2l+1=5$ (超过半满) , 按倒转次序取 $J=L+S=4$ , 基态为 ${}^5{D}_4$ .

$jj$ 耦合

当自旋轨道相互作用强于剩余静电势时, 先耦合前者, 再考虑后者.

适用于重原子激发态

每个电子 $i$ 的自旋 ${\vec{s}}_i$ 和它自身的轨道角动量 ${\vec{l}}_i$ 之间的相互作用非常强. 它们会优先耦合在一起, 形成每个电子的总角动量 ${\vec{j}}_i={\vec{l}}_i+{\vec{s}}_i$ .在这个阶段, ${\vec{l}}_i$ 和 ${\vec{s}}_i$ 都不守恒 (它们围绕 ${\vec{j}}_i$ 快速进动) , 但 ${\vec{j}}_i$ 的大小 $j_i$ 是守恒的. 每个电子就像一个独立的, 自旋轨道耦合了的粒子. 也就是说, ${\vec{j}}_i$ 向量本身在只考虑自旋-轨道作用时是相对稳定的.

现在, 这些已经形成了 ${\vec{j}}_i$ 的电子之间, 还存在较弱的剩余静电相互作用. 这个相互作用使得这些 ${\vec{j}}_i$ 向量之间发生耦合. 所有的 ${\vec{j}}_i$ 耦合起来形成原子的总角动量 $\vec{J}=\sum {\vec{j}}_i$ . 由于剩余静电势的作用, 单个的 ${\vec{j}}_i$ 不再守恒 (它们开始围绕 $\vec{J}$ 进动) , 但最终的总角动量 $\vec{J}$ 是守恒的.

$jj$ 耦合的总体图像就是快速的 $({\vec{l}}_i,{\vec{s}}_i\to {\vec{j}}_i)$ 耦合, 然后是慢速的 $({\vec{j}}_i\to \vec{J})$ 耦合.

例子

试给出3p4d的$jj$耦合情况

对3p电子, 自旋-轨道相互作用耦合 ($S=\frac{1}{2},l=1$) 给出: $j_1=\frac{1}{2}$ 和 $\frac{3}{2}$.

对4d电子, 自旋—轨道相互作用耦合 ($S=\frac{1}{2},l=2$) 给出: $j_2=\frac{3}{2}$ 和 $\frac{5}{2}$.

因此,3p4d 在 $jj$ 耦合下的原子态为 $(\frac{1}{2},\frac{3}{2}{)}_{2,1}$ $(\frac{1}{2},\frac{5}{2}{)}_{3,2}$ $(\frac{3}{2},\frac{3}{2}{)}_{3,2,1,0}$ $(\frac{3}{2},\frac{5}{2}{)}_{4,3,2,1}$. 这里的下标表示总角动量量子数 $J$ 可能的取值, 如对于最后一个原子态 $J$ 可以取 $\left|\frac{5}{2}-\frac{3}{2}\right|$ 到 $\left|\frac{5}{2}+\frac{3}{2}\right|$ 之间的所有整数值.

选择定则

LS 耦合的选择定则

LS 耦合适用于轻原子 (低 $Z$ 原子) , 其中自旋-轨道相互作用较弱, 电子间的库仑相互作用占主导. 其选择定则为:

$$\{\begin{array}{ll}\Delta ({\sum }_i{l}_i)=\pm 1& \text{ (跃迁电子的轨道角动量变化) }\\ \Delta S=0& \text{ (总自旋量子数不变) }\\ \Delta L=0,\pm 1& \text{ (总轨道角动量变化, 但 }0\leftrightarrow 0\text{ 禁戒) }\\ \Delta J=0,\pm 1& \text{ (总角动量变化, 但 }0\leftrightarrow 0\text{ 禁戒) }\\ \Delta M_J=0,\pm 1& \text{ (磁量子数变化, }\Delta J=0\text{ 时 }0\leftrightarrow 0\text{ 禁戒) }\end{array}$$

物理意义

• $\Delta ({\sum }_i{l}_i)=\pm 1$: 电偶极跃迁要求 单个电子 的轨道角动量 $l$ 改变 $\pm 1$ (例如 $s\leftrightarrow p$ , $p\leftrightarrow d$ 等) .
• $\Delta S=0$: 自旋方向不改变, 因此 单重态 ( $S=0$ ) 只能跃迁到单重态, 三重态 ( $S=1$ ) 只能跃迁到三重态.
• $\Delta L=0,\pm 1$: 总轨道角动量可以不变或改变 $\pm 1$ , 但 $L=0\leftrightarrow L=0$ 的跃迁是禁戒的.
• $\Delta J=0,\pm 1$: 总角动量可以不变或改变 $\pm 1$ , 但 $J=0\leftrightarrow J=0$ 的跃迁是禁戒的 (因为光子携带角动量 $1\hslash$ ) .
• $\Delta M_J$ 规则: 仅在外场 (如磁场) 存在时才需要考虑.

$jj$ 耦合的选择定则

$jj$ 耦合适用于重原子 (高 $Z$ 原子) , 其中自旋-轨道相互作用较强, 单个电子的 $l$ 和 $s$ 先耦合形成 $j$ , 再与其他电子的 $j$ 耦合. 其选择定则为:

$$\{\begin{array}{ll}\Delta ({\sum }_i{l}_i)=\pm 1& \text{ (跃迁电子的轨道角动量变化) }\\ \Delta j=0,\pm 1& \text{ (跃迁电子的 }j\text{ 变化) }\\ \Delta J=0,\pm 1& \text{ (总角动量变化, 但 }0\leftrightarrow 0\text{ 禁戒) }\\ \Delta M_J=0,\pm 1& \text{ (磁量子数变化, }\Delta J=0\text{ 时 }0\leftrightarrow 0\text{ 禁戒) }\end{array}$$

物理意义

• $\Delta j=0,\pm 1$: 单个电子的总角动量 $j$ 可以不变或改变 $\pm 1$ (例如 $j=1/2\leftrightarrow j=1/2$ 或 $j=1/2\leftrightarrow j=3/2$ ) .
• 其他规则 ( $\Delta J$ , $\Delta M_J$ ) 与 LS 耦合类似.

共同点与区别

规则	LS 耦合	jj 耦合
**$\Delta l$ **	$\pm 1$	$\pm 1$
**$\Delta S$ **	$0$	无限制
**$\Delta L$ **	$0,\pm 1$	无限制
**$\Delta j$ **	无限制	$0,\pm 1$ (跃迁电子)
**$\Delta J$ **	$0,\pm 1$	$0,\pm 1$
**$\Delta M_J$ **	$0,\pm 1$	$0,\pm 1$