Thermodynamics Midterm Review

技巧

计算压强时选取$p$的单位为水柱或者汞柱, 使得系数$\rho g=1$

导论

Introduction to Thermodynamics

系统的分类

封闭系统 vs 绝热系统 vs 孤立系统 单元 vs 多元 均匀 vs 非均匀

宏观量是系统相应微观量的统计平均值

温度和平衡态

Temperature and Equilibrium State

平衡态

平衡态 vs 稳定态

平衡态是孤立体系, 稳定态只是宏观状态不变（如夹在热源和冷源之间的金属棒, 温度分布稳定但是有热流）

弛豫时间? 动态平衡

微观量一直在变, 但是宏观统计量不变

三个平衡条件?

力 热 化学

热平衡

热平衡?

通过传热达成的平衡态

热力学第零定律? 经验温标?

经验上以某一种物质属性随温度的变化为依据并用经验公式进行分度的温标统称经验温标

温标三要素?

测温属性需随温度有单调的、连续的、显著的变化. 固定点 对测温属性随温度的变化关系作出规定

理想气体温标

固定点? 水的三相点 局限性?

气压越低、气体越稀薄越准确；不能用于测量极低温和极高温

热力学温标?

国际实用温标?

物态方程

理想气体物态方程 Dalton 分压定律

响应函数

体膨胀系数

$$\alpha =\frac{1}{V}{\left(\frac{\partial V}{\partial T}\right)}_p$$

压强系数

$$\beta =\frac{1}{p}{\left(\frac{\partial p}{\partial T}\right)}_V$$

等温压缩系数

$${\kappa }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial p}\right)}_T$$

分子动理论

三相

固体: 较低温度下, 分子的无规则运动不够剧烈, 分子在相互作用力的影响下被束缚在各自的平衡位置附近做微小的振动, 表现为固体状态.

液体: 温度升高, 无规则运动剧烈到某一限度时, 分子力的作用已不能把分子束缚在固定的平衡位置附近做微小的振动, 但还不能使分子分散远离, 表现为液体状态.

气体: 温度再升高, 无规则运动进一步剧烈到一定限度时, 不但分子的平衡位置没有了, 而且分子之间也不能再维持一定的距离, 这时分子互相分散远离, 分子的运动近似为自由运动, 表现为气体状态.

Brown 运动 vs 分子热运动

宏观 vs 微观

压强公式

$$p=\frac{2}{3}n\bar{\epsilon };p=n{k}_{B}T$$

方均根速率

$$\sqrt{\overline{v^2}}=\sqrt{\frac{3k_{B}T}{m_0}}$$

数量级为$10^3\text{ m}/\mathrm{s}$

Van der Waals 方程

分子势能 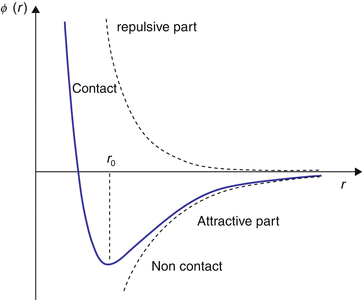分子有效直径$d$满足

$$E_p{|}_{r=d}=E_{k0}$$

Van der Waals 方程

$$(p+\frac{a}{V_m^2})(V_m-b)=RT$$

左边的修正是对压强的修正, 考虑了分子间吸引力 右边的修正是对体积的修正, 考虑了气体分子间隙（分子间斥力）

$$b=4N_A{V}_0,V_0=\frac{4}{3}\pi {\left(\frac{d}{2}\right)}^2$$

Maxwell 速度分布律

讨论的是在平衡态时的速度分布

含义

$$\mathrm{d}P(v_x,v_y,v_z)=\frac{\mathrm{d}N}{N(v_x,y_y,v_z)}=f(v_x,v_y,v_z)\mathrm{d}{v}_x\mathrm{d}{v}_y\mathrm{d}{v}_z$$

即概率密度乘上自变量的小量后得到概率, 对某一上下限积分就得到在该积分限内的概率

分布应该满足的条件

• 分布各向同性, 只和速度大小有关

$$f(v_x,v_y,v_z)=F(v_x^2+v_y^2+v_z^2)=F(v^2)$$

• 三个方向上的速度分量相互独立

$$f(v_x,v_y,v_z)=\varphi (v_x)\varphi (v_y)\varphi (y_z)=g(v_x^2)g(v_y^2)g(v_z^2)$$

• $v^2\to 0⟹F(v^2)\to 0$
• 再通过归一化条件和能量条件给出两个系数

速度分布律

$$\boxed{f(v_x)={\left(\frac{m_0}{2k_{B}T}\right)}^{1/2}\exp \left(-\frac{m_0}{2k_{B}T}{v}_x^2\right)}$$

或者

$$\boxed{f(v_x,v_y,v_z)={\left(\frac{m_0}{2k_{B}T}\right)}^{3/2}\exp \left[-\frac{m_0}{2k_{B}T}(v_x^2+v_y^2+v_z^2)\right]}$$

速率分布律

$$f_M(v)=4\pi v^2{\left(\frac{m_0}{2\boxed{\pi }{k}_{B}T}\right)}^{3/2}\exp \left(-\frac{m_0}{2k_{B}T}{v}^2\right)$$

特殊值

最概然速率

$$v_p=\sqrt{\frac{2k_{B}T}{m_0}}$$

平均速率

$$\bar{v}=\sqrt{\frac{8k_{B}T}{\pi m_0}}$$

方均根速率

$$\sqrt{\overline{v^2}}=\sqrt{\frac{3k_{B}T}{m_0}}$$

某个关于速度的物理量

的平均值

$$\overline{g(v)}=\frac{{\int }_{v_1}^{v_2}g(v)f(v)\mathrm{d}v}{{\int }_{v_1}^{v_2}f(v)\mathrm{d}v}$$

的分布

令$g(v)⟹v=g^{-1}$

$$f(g)\mathrm{d}g=\frac{\mathrm{d}N(g)}{N}=f_M(v)\mathrm{d}v=f(g^{-1})\mathrm{d}(g^{-1})$$

分子碰壁数

$$\Gamma =n{\int }_0^{\infty }{v}_x{f}_M(v_x)\mathrm{d}{v}_x=n\sqrt{\frac{k_{B}T}{2\pi m_0}}=\frac{1}{4}n\bar{v}$$

泻流

热分子压强差现象

一小孔连接两个装有同种气体的容器, 保持两边温度分别为$T_1$和$T_2$

• 达到稳定前, 气体分子从一个容器喷射向另一个容器形成的流动称为泻流 (effusion)
• 达到稳定后, 两容器中的气体压强不相等, 该现象称为热分子压强差现象

达到稳定时, 两边的分子碰壁数应相等, 因此有

$${\Gamma }_1={\Gamma }_2⟹\frac{p_1}{p_2}={\left(\frac{T_1}{T_2}\right)}^{1/2}$$

泻流分离

容器中装有温度为$T$的混合气体, 它由质量分别为$m_1$和$m_2$的两种组元组成, 则泻流分子束中两种组元的分子数目比

$$\frac{I_1}{I_2}=\frac{n_1{\bar{v}}_1}{n_2{\bar{v}}_2}=\frac{n_1}{n_2}\sqrt{\frac{m_2}{m_1}}$$

通过多次连续泻流, 可以提纯质量较轻的组元

$${\left(\frac{n_1}{n_2}\right)}_N=\frac{n_{10}}{n_{20}}{\left(\frac{m_2}{m_1}\right)}^{N/2}$$

Boltzmann 分布

Boltzmann 密度分布

把重力场中的密度函数推广到任意外场

$$f_B(\mathbf{r})=\frac{n_0}{N}{e}^{-{\epsilon }_p(\mathbf{r})/k_{B}T}$$

前面的系数可以由归一化条件给出

Boltzmann 分布律

微观粒子按速度$\mathbf{v}$的分布

$$f(\mathbf{v})={\left(\frac{m_0}{2k_{B}T}\right)}^{3/2}\exp \left[-\frac{m_0{v}^2}{2k_{B}T}\right]={\left(\frac{m_0}{2k_{B}T}\right)}^{3/2}\exp \left[-\frac{{\epsilon }_k(\mathbf{v})}{k_{B}T}\right]$$

按照位置$\mathbf{r}$的分布

$$f_B(\mathbf{r})=\frac{n_0}{N}\exp \left[-\frac{{\epsilon }_p(\mathbf{r})}{k_{B}T}\right]$$

二者相乘即为Boltzmann分布律

$$f_{MB}(\mathbf{v},\mathbf{r})=\frac{n}{N}{\left(\frac{m_0}{2\pi k_{B}T}\right)}^{3/2}\exp \left[-\frac{{\epsilon }_p(\mathbf{r})+{\epsilon }_k(\mathbf{v})}{k_{B}T}\right]$$

由此可以得到

$$\frac{\mathrm{d}N(\mathbf{v},\mathbf{r})}{N}=f_{MB}(\mathbf{v},\mathbf{r}){\mathrm{d}}^3\mathbf{v}{\mathrm{d}}^3\mathbf{r}$$

能量均分定理

振动自由度

$n$个原子构成的气体分子中的每一个原子质点都有$3$个总自由度, 故振动有$s=(3n-t-r)$个自由度

理想气体热容

定体摩尔热容

$$C_{V,m}=\frac{1}{2}(t+r+2s)R$$

对于非刚性的单原子和双原子理想气体, 其定体摩尔热容分别为$\frac{3}{2}R$和$\frac{7}{2}R$ 然而, 在常温下, 双原子气体的振动自由度未被激活, 所以一般取其$C_{V,m}=\frac{5}{2}R$ 且有

$$C_{p,m}=C_{V,m}+R$$

平均自由程

有效碰撞截面

由碰撞的双方共同决定

• 同种分子碰撞截面: $\sigma =\pi d^2$, 其中$d$为分子直径
• 不同种分子的碰撞截面: $\sigma =\pi {\left(\frac{d_1+d_2}{2}\right)}^2$

平均自由程

定义

• 碰撞频率$Z$: 一个分子在单位时间内与其他分子发生碰撞的次数
• 自由程$\lambda$: 一个分子在连续两次和其他分子发生碰撞之间经过的路程 引入平均自由飞行时间$\bar{\tau }=1/\bar{Z}$, 于是有

$$\bar{\lambda }=\bar{v}\cdot \bar{\tau }=\bar{v}/\bar{Z}$$

相对速率

平均相对速率 $\bar{u}=\sqrt{2}\bar{v}$

推导

在$\Delta t$时间内, 入射分子发生碰撞的数目为

$$n\Delta V=n\sigma \bar{u}\Delta t=\bar{Z}\Delta t$$

平均碰撞频率

$$\bar{Z}=n\sigma \bar{u}=\sqrt{2}n\sigma \bar{v}$$

于是有平均自由程

$$\bar{\lambda }=\bar{v}/\bar{Z}=\boxed{\frac{1}{\sqrt{2}\sigma n}}$$

又由理想气体状态方程, 有

$$\bar{\lambda }=\frac{\bar{v}}{\bar{Z}}=\frac{1}{\sqrt{2}\pi n{d}^2}=\frac{k_{B}T}{\sqrt{2}\pi p{d}^2}$$

混合气体的平均自由程

	A 类分子	B 类分子
与A碰撞的平均频率	${\bar{Z}}_{AA}=n_A\pi d_A^2{\bar{u}}_{AA}$	${\bar{Z}}_{BA}=n_A\pi d_{AB}^2{\bar{u}}_{AB}$
与B碰撞的平均频率	${\bar{Z}}_{BA}=n_B\pi d_{AB}^2{\bar{u}}_{AB}$	${\bar{Z}}_{BB}=n_B\pi d_B^2{\bar{u}}_{BB}$
平均自由程	${\bar{\lambda }}_A={\bar{v}}_A/({\bar{Z}}_{AA}+{\bar{Z}}_{AB})$	${\bar{\lambda }}_B={\bar{v}}_B/({\bar{Z}}_{BA}+{\bar{Z}}_{BB})$
则混合气体的平均自由程则是这两种分子的算术平均值

$$\bar{\lambda }=\frac{n_A{\bar{\lambda }}_A+n_B{\bar{\lambda }}_B}{n_A+n_B}$$

气体按自由程的分布

• 设想在某一个时刻的一组分子有$N$个
• 在后面的运动过程中, 任一分子和其他分子发生碰撞, 则将其剔除出去, 该组分子就减少一个
• 设这组分子通过路径$\lambda$后还剩下$N(\lambda )$个, 而在下一段路程$\mathrm{d}\lambda$中, 分子数又改变了$\mathrm{d}N(\lambda )$
• $N(\lambda )$即为通过路程$\lambda$后还未发生碰撞的粒子数目, 即自由程大于$\lambda$的分子数目
• 在路程$\lambda \sim \lambda +\mathrm{d}\lambda$ 之间, 由于平均而言每个分子走过$\bar{\lambda }$距离会发生一次碰撞, 所以在这段路程中每个分子发生碰撞的概率为$\frac{\mathrm{d}\lambda }{\bar{\lambda }}$ 由此可以推出

$$-\mathrm{d}N(\lambda )=N(\lambda )\frac{\mathrm{d}\lambda }{\bar{\lambda }}⟹N(\lambda )=C{e}^{-\lambda /\bar{\lambda }}=N{e}^{-\lambda /\bar{\lambda }}$$

于是

$$-\frac{\mathrm{d}N(\lambda )}{N}=\frac{1}{\bar{\lambda }}{e}^{-\lambda /\bar{\lambda }}\mathrm{d}\lambda =f(\lambda )\mathrm{d}\lambda ⟹\boxed{f(\lambda )=\frac{1}{\bar{\lambda }}{e}^{-\lambda /\bar{\lambda }}}$$

输运过程

分类

热传导

系统各区域温度不均匀而使能量（热量） 从高温区域传递到低温区域的现象, 每一个分子传递的是动能（$c_{V}mT$, $c_V=\frac{C_V}{m}$）

扩散

系统各区域浓度不均匀而使质量（粒子） 从浓度高的区域传递到低浓度区域的现象, 每一个分子传递的是质量

压强扩散

扩散过程中系统的压强分布不均匀 密度不均匀$\to$数密度不均匀$\to$压强不均匀$\to$宏观气流

如一种气体在真空中的扩散

纯扩散

扩散过程中系统的压强、温度分布均匀且恒定, 无宏观气流 扩散是由于分子热运动导致的

如种理想气体在某定容容器中之间的隔板被移除后的扩散

黏性

系统各区域粒子定向速度不均匀而使动量从动量高的区域传递到低动量区域的现象, 每一个分子传递的是定向移动的动量（$m\mathbf{u}$, 其中$\mathbf{u}$是定向移动速度）

Newton 定律

$$F(z)=-\eta \left(\frac{\mathrm{d}u}{\mathrm{d}z}\right)\mathrm{d}S$$

Fourier 定律

$$\frac{\mathrm{d}Q}{\mathrm{d}t}=-\kappa {\left(\frac{\mathrm{d}T}{\mathrm{d}z}\right)}_{z_0}\mathrm{d}S$$

Fick 定律

$$\frac{\mathrm{d}}{\mathrm{d}{N}_{\alpha }}t=-D_{\alpha \beta }\left(\frac{\mathrm{d}{n}_{\alpha }}{\mathrm{d}z}\right)\mathrm{d}S$$

Tip

从一侧移向另一侧的分子数$=$碰壁数$+$扩散效应（Fick 定律给出的一半）

$$\mathrm{d}N=\left(\frac{1}{6}n\bar{v}+\frac{1}{6}\bar{\lambda }\frac{\mathrm{d}n}{\mathrm{d}z}\right)\mathrm{d}S$$

注意在输运过程中课本采用$\Gamma =n\bar{v}/6$

系数取值

$$\begin{array}{c}\eta =\frac{1}{3}\rho \bar{v}\lambda \\ \kappa =\frac{1}{3}\rho \bar{v}\lambda c_V,c_V=C_V/m\\ D=\frac{1}{3}\bar{v}\lambda \end{array}$$