Progressive Distillation for Fast Sampling of Diffusion Models

Progressive Distillation Method

Idea

The core idea involves a distillation process where a pre-trained "teacher" model, which requires a high number of sampling steps (up to 8192), is used to train a "student" model that takes significantly fewer steps. This distillation is progressively applied, effectively halving the number of required sampling steps at each iteration. Remarkably, this approach allows for models that can generate samples in as few as 4 steps while still maintaining high perceptual quality

Method

Require:

• Trained teacher model ${\hat{x}}_{\eta }(z_t)$
• Data set $\mathcal{D}$
• Loss weight function $w()$
• Student sampling steps $N$

---

For $K$ iterations do

1. $\theta \leftarrow \eta$ ⟶ Init student from teacher While not converged do
   • $\mathbf{x}\sim \mathcal{D}$
   • $t=i/N,i\sim \text{Cat}[1,2,\dots ,N]$
   • $ϵ\sim \mathcal{N}(0,\mathbb{I})$
   • $z_t={\alpha }_t\mathbf{x}+{\sigma }_tϵ$
   • 2 steps of DDIM with teacher
   • $t^{\prime }=t-0.5/N,t^{\prime \prime }=t-1/N$
   • $z_{t^{\prime }}={\alpha }_{t^{\prime }}{\hat{x}}_{\eta }(z_t)+\frac{{\sigma }_{t^{\prime }}}{{\sigma }_t}(z_t-{\alpha }_t{\hat{x}}_{\eta }(z_t))$
   • $z_{t^{\prime \prime }}={\alpha }_{t^{\prime \prime }}{\hat{x}}_{\eta }(z_{t^{\prime }})+\frac{{\sigma }_{t^{\prime \prime }}}{{\sigma }_{t^{\prime }}}(z_{t^{\prime }}-{\alpha }_{t^{\prime }}{\hat{x}}_{\eta }(z_{t^{\prime }}))$
   • $\hat{x}=\frac{z_t^{\prime \prime }-({\sigma }_{t^{\prime \prime }}/{\sigma }_t)z_t}{{\alpha }_{t^{\prime \prime }}-({\sigma }_{t^{\prime }}/{\sigma }_t){\alpha }_t}$ ⟶ Teacher $\hat{x}$ target
   • ${\lambda }_t=\log \left(\frac{{\alpha }_t^2}{{\sigma }_t^2}\right)$
   • $L_{\theta }=w({\lambda }_t){\Vert \hat{x}-{\hat{x}}_{\theta }(z_t)\Vert }_2^2$
   • $\theta \leftarrow \theta -\gamma {\nabla }_{\theta }{L}_{\theta }$ End while
2. $\eta \leftarrow \theta$ ⟶ Student becomes next teacher
3. $N\leftarrow N/2$ ⟶ Halve number of sampling steps End for

---

Where the target $\hat{x}$ is set to $\frac{z_t^{\prime \prime }-({\sigma }_{t^{\prime \prime }}/{\sigma }_t)z_t}{{\alpha }_{t^{\prime \prime }}-({\sigma }_{t^{\prime }}/{\sigma }_t){\alpha }_t}$ such that if we use the student model to sample $1$ DDIM step from $z_t$ using the mean determined by $\hat{x}$ (with zero variance in DDIM), then the denoised result $z_{t^{\prime }}^{\prime }$ should equal to $z_{t^{\prime \prime }}$, which the the denoised result of the teacher model after $2$ DDIM steps with the mean determined by ${\hat{x}}_{\eta }$

New parameterization method: v-prediction

Idea

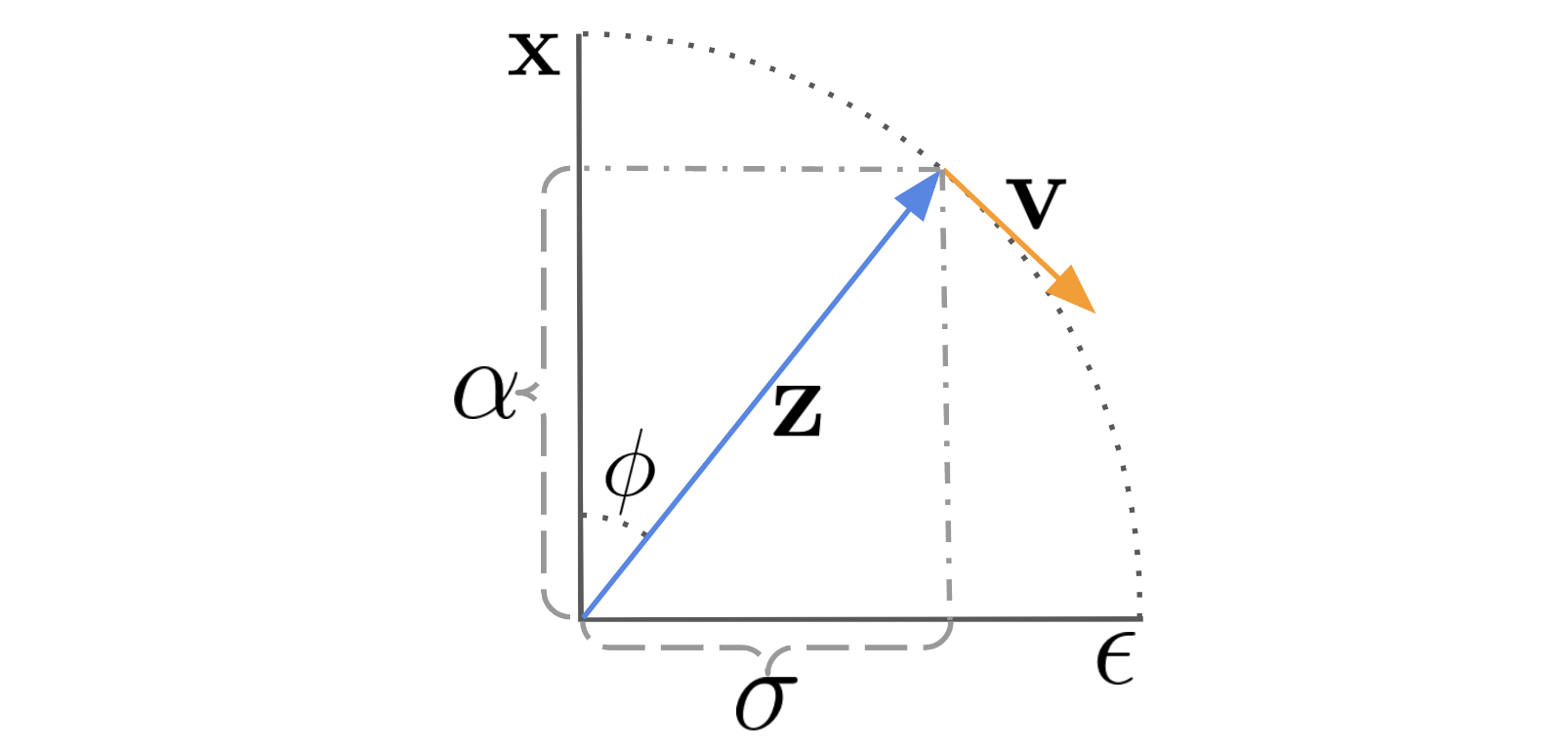
The authors proposed an alternative method of v-prediction, which involves predicting a latent variable $v$ instead of directly predicting the noise $ϵ$. This approach provides more stable training dynamics, particularly when distilling diffusion models to fewer steps. The relationship between $v$ and $ϵ$ is defined through the following key ideas:

• $v$ is a transformation of both the original data and the noise.
• By predicting $v$, the model can smoothly transition between steps, allowing it to interpolate between predicting the noise $ϵ$ directly and predicting the clean data.

Formulation

For two times $s,t\in [0,1]$, we want to update from $t$ to $s$ ($t>s$), and the update rule given by DDIM is

$$z_s={\alpha }_s{x}_s+{\sigma }_s{ϵ}_s={\alpha }_s{\hat{x}}_{\theta }(z_t)+{\sigma }_s\frac{z_t-{\alpha }_t{\hat{x}}_{\theta }(z_t)}{{\sigma }_t}$$

We can simplify the DDIM update rule by expressing it in terms of ${\varphi }_t=\arctan ({\sigma }_t/{\alpha }_t)$. Assuming a variance preserving diffusion process, we have ${\alpha }_{\varphi }=\cos (\varphi ),{\sigma }_{\varphi }=\sin (\varphi )$, and hence

$$z_{\varphi }=\cos (\varphi )x+\sin (\varphi )ϵ$$

And we define the velocity of $z_{\varphi }$

$$v_{\varphi }=\frac{\mathrm{d}{z}_{\varphi }}{\mathrm{d}\varphi }=\cos (\varphi )ϵ-\sin (\varphi )x$$

Furthermore, we define the predicted velocity as

$${\hat{v}}_{\theta }(z_{\varphi })=\cos (\varphi ){\widehat{ϵ}}_{\theta }(z_{\varphi })-\sin (\varphi ){\hat{x}}_{\theta }(z_{\varphi })$$

where ${\widehat{ϵ}}_{\theta }(z_{\varphi })=(z_{\varphi }-\cos (\varphi ){\hat{x}}_{\theta }(z_{\varphi }))/\sin (\varphi )$. And now we have

$$\begin{array}{rl}{z}_{{\varphi }_s}& =\cos ({\varphi }_s){\hat{x}}_{\theta }(z_{{\varphi }_t})+\sin ({\varphi }_s){\widehat{ϵ}}_{\theta }(z_{{\varphi }_t})\\ & =\cos ({\varphi }_s)\left(\cos ({\varphi }_t)z_{{\varphi }_t}-\sin ({\varphi }_t){\hat{v}}_{\theta }(z_{{\varphi }_t})\right)+\sin ({\varphi }_s)\left(\sin ({\varphi }_t)z_{{\varphi }_t}+\cos ({\varphi }_t){\hat{v}}_{\theta }(z_{{\varphi }_t})\right)\\ & =\cos ({\varphi }_s-{\varphi }_t)z_{{\varphi }_t}+\sin ({\varphi }_s-{\varphi }_t){\hat{v}}_{\theta }(z_{{\varphi }_t})\end{array}$$

Viewed from this perspective, DDIM thus evolves $z_{{\varphi }_s}$ by moving it on a circle in the $(z_{{\varphi }_t},{\hat{v}}_{{\varphi }_t})$ basis, along the $-{\hat{v}}_{{\varphi }_t}$ direction, gradually denoising smoothly towards $x$