Back-propagation

Preliminaries on Partial Derivatives

Suppose a scalar variable $J$ depend on some variables $z$, we write $\frac{\partial J}{\partial z}$ as the partial derivatives of $J$. We stress that the convention here is that $\frac{\partial J}{\partial z}$ has exactly the same dimension as $z$ itself. For example, if $z\in {\mathbb{R}}^{m\times n}$, then $\frac{\partial J}{\partial z}\in {\mathbb{R}}^{m\times n}$, and the $(i,j)$-entry of $\frac{\partial J}{\partial z}$ is equal to $\frac{\partial J}{\partial z_{i,j}}$.

Chain rule

Consider a scalar variable $J$ which is obtained by the composition of $f$ and $g$ on some variable $z$

$$z\in {\mathbb{R}}^m\to u=g(z)\in {\mathbb{R}}^m\to J=f(u)\in {\mathbb{R}}^m$$

Let $u=(u_1,\dots ,u_n)$ and let $g(z)=(g_1(z),\dots ,g_n(z))$, then the standard chain rule gives us that

$$\forall i\in \left\{1,\dots ,m\right\},\frac{\partial J}{\partial z_i}=\sum _{j=1}^n\frac{\partial J}{\partial u_j}\frac{\partial g_j}{\partial z_i}$$

or in a vectorized notation

$$\frac{\partial J}{\partial z}=\left(\begin{array}{ccc}\frac{\partial g_1}{\partial z_1}& \cdots & \frac{\partial g_n}{\partial z_1}\\ ⋮& \ddots & ⋮\\ \frac{\partial g_1}{\partial z_m}& \cdots & \frac{\partial g_n}{\partial z_m}\end{array}\right)\cdot \frac{\partial J}{\partial u}$$

In other words, the backward function is always a linear map from $\frac{\partial J}{\partial u}$ to $\frac{\partial J}{\partial z}$.

Key interpretation of the chain rule

We can view the formula above as a way to compute $\frac{\partial J}{\partial z}$ from $\frac{\partial J}{\partial u}$

$$\frac{\partial J}{\partial u}\underset{\text{only requires info about g(⋅) and z}}{\overset{\text{chain rule}}{\to }}\frac{\partial J}{\partial z}$$

Moreover, this formula only involves knowledge about $g$ (more precisely $\frac{\partial g_j}{\partial z_i}$).

We use $\mathcal{B}[g,z]$ to define the function that maps $\frac{\partial J}{\partial u}$ to $\frac{\partial J}{\partial z}$, and write

$$\frac{\partial J}{\partial z}=\mathcal{B}[g,z]\left(\frac{\partial J}{\partial u}\right)$$

We call $\mathcal{B}[g,z]$ the backward function for the module $g$. Note that when $z$ is fixed, $\mathcal{B}[g,z]$ is merely a linear map from ${\mathbb{R}}^n$ to ${\mathbb{R}}^n$

$${\left(\mathcal{B}[g,z](v)\right)}_i=\sum _{j=1}^n\frac{\partial g_i}{\partial z_i}\cdot v_j$$

General strategy of back-propagation

We take the viewpoint that neural networks are complex compositions of small building blocks such as MM, $\sigma$, Conv2D, LN etc., then we can abstractly write the loss function $J$ (on a single example $(x,y)$) as a composition of many modules

$$J=M_k\left(M_{k-1}\left(\cdots M_1(x)\right)\right)$$

We assume that each $M_i$ involves a set of parameters ${\theta }^{[i]}$, though ${\theta }^{[i]}$ could possibly be an empty set when $M_i$ is a fixed operation such as the non-linear activations.

We introduce the intermediate variables for the composition

$$\begin{array}{rl}{u}^{[0]}& =x\\ u^{[1]}& =M_1\left(u^{[0]}\right)\\ u^{[2]}& =M_2\left(u^{[1]}\right)\\ & ⋮\\ J=u^{[k]}& =M_k\left(u^{[k-1]}\right)\end{array}$$

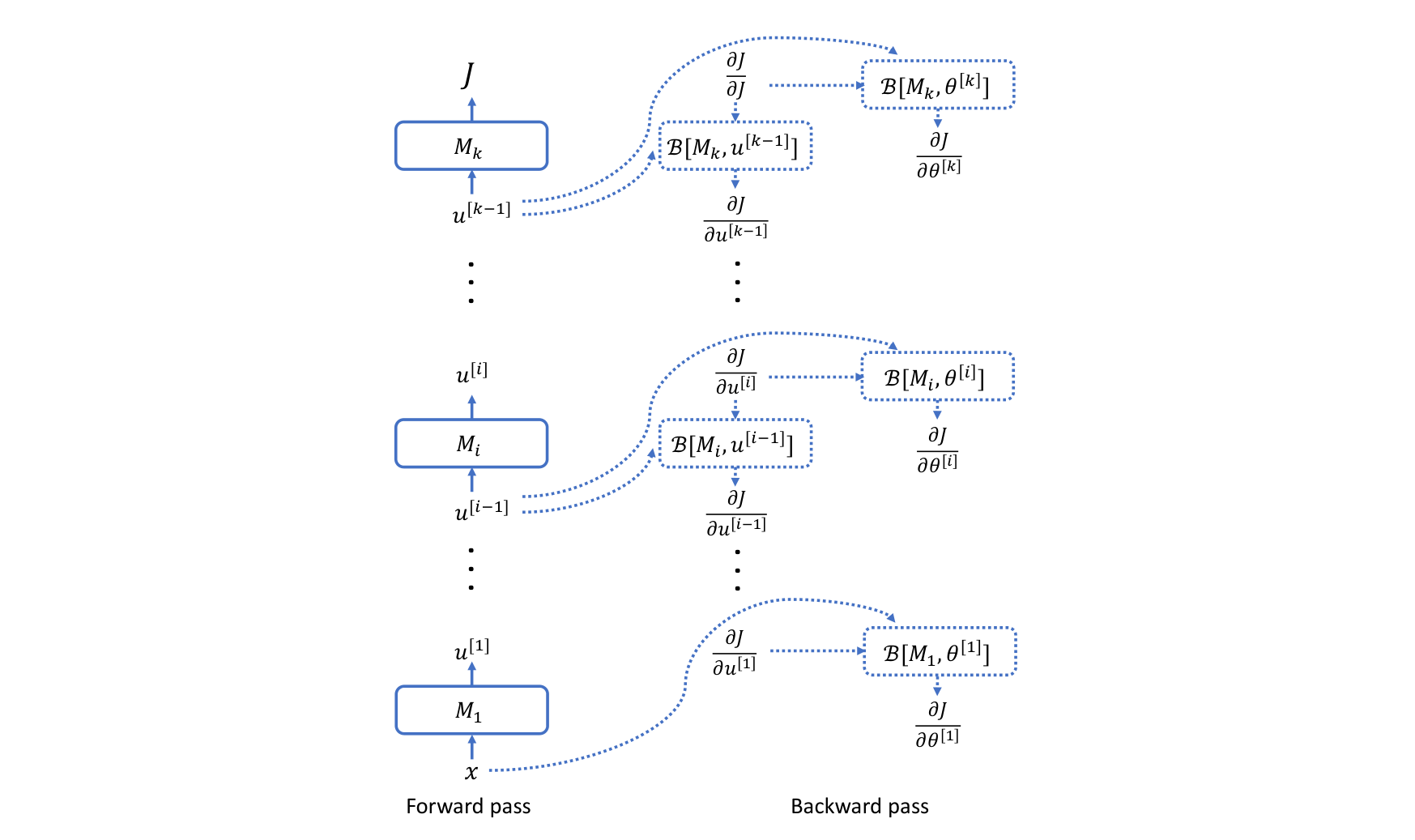
Back-propagation consists of two passes. In the forward pass, the algorithm simply computes $u^{[1]},\dots ,u^{[k]}$ from $i=1,\dots ,k$, and save all the intermediate variables $u^{[i]}$'s in the memory.

In the backward pass, we first compute the derivatives w.r.t to the intermediate variables, that is, $\frac{\partial J}{\partial u^{[k]}},\dots ,\frac{\partial J}{\partial u^{[1]}}$, sequentially in this backward order, and then compute the derivatives of the parameters $\frac{\partial J}{\partial {\theta }^{[i]}}$ form $\frac{\partial J}{\partial u^{[i]}}$ and $u^{[i-1]}$. These two type of computations can be also interleaved with each other because $\frac{\partial J}{\partial {\theta }^{[i]}}$ only depends on $\frac{\partial J}{\partial u^{[i]}}$ and $u^{[i-1]}$.

We first see why $\frac{\partial J}{\partial u^{[i-1]}}$ can be computed efficiently from $\frac{\partial J}{\partial u^{[i]}}$ and $u^{[i-1]}$ by invoking the discussion on the chain rule. We instantiate the discussion by setting $u=u^{[i]}$ and $z=u^{[i-1]}$, and $f(u)=M_k(M_{k-1}(\cdots M_{i+1}(u^{[i]})))$, and $g(\cdot )=M_i(\cdot )$. Note that $f$ is very complex but we don't need any concrete information about $f$. Then, the conclusive equation corresponds to

$$\frac{\partial J}{\partial u^{[i]}}\underset{\text{only requires info about }{M}_i(\cdot )\text{ and }{u}^{[i-1]}}{\overset{\text{chain rule}}{\to }}\frac{\partial J}{\partial u^{[i-1]}}$$

More precisely, we can write

$$\frac{\partial J}{\partial u^{[i-1]}}=\mathcal{B}[M_i,u^{[i-1]}]\left(\frac{\partial J}{\partial u^{[i]}}\right).$$

Instantiating the chain rule with $z={\theta }^{[i]}$ and $u=u^{[i]}$, we also have

$$\frac{\partial J}{\partial {\theta }^{[i]}}=\mathcal{B}[M_i,{\theta }^{[i]}]\left(\frac{\partial J}{\partial u^{[i]}}\right).$$

Example Code

#include <vector>
#include <memory>
 
// Base class for a module
class Module {
public:
    virtual ~Module() = default;
 
    // Forward pass: computes output given input
    virtual std::vector<double> forward(const std::vector<double>& input) = 0;
 
    // Backward pass: computes gradients of input and parameters
    virtual std::vector<double> backward(const std::vector<double>& grad_output) = 0;
 
    // Update parameters using gradients
    virtual void update_parameters(double learning_rate) = 0;
};
 
// Neural network class
class NeuralNetwork {
private:
    std::vector<std::shared_ptr<Module>> modules;
    std::vector<std::vector<double>> intermediate_outputs;
 
public:
    void add_module(std::shared_ptr<Module> module) {
        modules.push_back(module);
    }
 
    // Forward pass
    std::vector<double> forward(const std::vector<double>& input) {
        intermediate_outputs.clear();
        std::vector<double> current_output = input;
        intermediate_outputs.push_back(current_output); // Save input
 
        for (const auto& module : modules) {
            current_output = module->forward(current_output);
            intermediate_outputs.push_back(current_output); // Save intermediate output
        }
 
        return current_output; // Final output (loss)
    }
 
    // Backward pass
    void backward(const std::vector<double>& grad_loss) {
        std::vector<double> current_grad = grad_loss;
 
        for (int i = modules.size() - 1; i >= 0; --i) {
            current_grad = modules[i]->backward(current_grad);
        }
    }
 
    // Update parameters
    void update_parameters(double learning_rate) {
        for (const auto& module : modules) {
            module->update_parameters(learning_rate);
        }
    }
};
 
// Example usage
int main() {
    NeuralNetwork network;
    // Add modules to the network (e.g., Linear, ReLU, etc.)
    // network.add_module(std::make_shared<Linear>(...));
    // network.add_module(std::make_shared<ReLU>());
 
    // Forward pass
    std::vector<double> input = { /* input data */ };
    std::vector<double> output = network.forward(input);
 
    // Compute loss gradient (e.g., using a loss function)
    std::vector<double> grad_loss = { /* gradient of loss w.r.t. output */ };
 
    // Backward pass
    network.backward(grad_loss);
 
    // Update parameters
    double learning_rate = 0.01;
    network.update_parameters(learning_rate);
 
    return 0;
}
 

#include <vector>
#include <memory>
#include <random>
#include <iostream>
#include <stdexcept>
 
class Linear : public Module {
private:
    std::vector<std::vector<double>> weights; // Weight matrix (W)
    std::vector<double> bias;                 // Bias vector (b)
    std::vector<double> input;                // Saved input for backward pass
    std::vector<std::vector<double>> grad_weights; // Gradient of weights
    std::vector<double> grad_bias;            // Gradient of bias
 
public:
    // Constructor: Initializes weights and biases randomly
    Linear(int input_size, int output_size) {
        // Initialize weights and biases with random values
        std::random_device rd;
        std::mt19937 gen(rd());
        std::normal_distribution<double> dist(0.0, 0.01);
 
        weights.resize(output_size, std::vector<double>(input_size));
        for (int i = 0; i < output_size; ++i) {
            for (int j = 0; j < input_size; ++j) {
                weights[i][j] = dist(gen);
            }
        }
 
        bias.resize(output_size);
        for (int i = 0; i < output_size; ++i) {
            bias[i] = dist(gen);
        }
 
        // Initialize gradients to zero
        grad_weights.resize(output_size, std::vector<double>(input_size, 0.0));
        grad_bias.resize(output_size, 0.0);
    }
 
    // Forward pass: Computes y = Wx + b
    std::vector<double> forward(const std::vector<double>& input) override {
        if (input.size() != weights[0].size()) {
            throw std::invalid_argument("Input size does not match weight matrix dimensions.");
        }
 
        this->input = input; // Save input for backward pass
 
        std::vector<double> output(weights.size(), 0.0);
 
        for (int i = 0; i < weights.size(); ++i) {
            for (int j = 0; j < input.size(); ++j) {
                output[i] += weights[i][j] * input[j];
            }
            output[i] += bias[i];
        }
 
        return output;
    }
 
    // Backward pass: Computes gradients of input, weights, and bias
    std::vector<double> backward(const std::vector<double>& grad_output) override {
        if (grad_output.size() != weights.size()) {
            throw std::invalid_argument("Gradient output size does not match weight matrix dimensions.");
        }
 
        std::vector<double> grad_input(weights[0].size(), 0.0);
 
        // Compute gradient of input
        for (int j = 0; j < weights[0].size(); ++j) {
            for (int i = 0; i < weights.size(); ++i) {
                grad_input[j] += weights[i][j] * grad_output[i];
            }
        }
 
        // Compute gradient of weights
        for (int i = 0; i < weights.size(); ++i) {
            for (int j = 0; j < weights[0].size(); ++j) {
                grad_weights[i][j] += grad_output[i] * input[j];
            }
        }
 
        // Compute gradient of bias
        for (int i = 0; i < weights.size(); ++i) {
            grad_bias[i] += grad_output[i];
        }
 
        return grad_input;
    }
 
    // Update parameters using gradients and learning rate
    void update_parameters(double learning_rate) override {
        for (int i = 0; i < weights.size(); ++i) {
            for (int j = 0; j < weights[0].size(); ++j) {
                weights[i][j] -= learning_rate * grad_weights[i][j];
            }
        }
 
        for (int i = 0; i < bias.size(); ++i) {
            bias[i] -= learning_rate * grad_bias[i];
        }
 
        // Reset gradients to zero
        for (int i = 0; i < weights.size(); ++i) {
            for (int j = 0; j < weights[0].size(); ++j) {
                grad_weights[i][j] = 0.0;
            }
        }
 
        for (int i = 0; i < bias.size(); ++i) {
            grad_bias[i] = 0.0;
        }
    }
 
    // Utility function to print weights and biases
    void print_parameters() const {
        std::cout << "Weights:" << std::endl;
        for (const auto& row : weights) {
            for (double val : row) {
                std::cout << val << " ";
            }
            std::cout << std::endl;
        }
 
        std::cout << "Biases:" << std::endl;
        for (double val : bias) {
            std::cout << val << " ";
        }
        std::cout << std::endl;
    }
};
 
// Example usage
int main() {
    Linear linear_layer(3, 2); // Input size = 3, Output size = 2
    std::vector<double> input = {1.0, 2.0, 3.0};
 
    // Forward pass
    std::vector<double> output = linear_layer.forward(input);
    std::cout << "Output:" << std::endl;
    for (double val : output) {
        std::cout << val << " ";
    }
    std::cout << std::endl;
 
    // Backward pass (dummy gradient)
    std::vector<double> grad_output = {0.1, 0.2};
    linear_layer.backward(grad_output);
 
    // Update parameters
    linear_layer.update_parameters(0.01);
 
    // Print updated parameters
    linear_layer.print_parameters();
 
    return 0;
}