Graph Connectivity

Paths

Let $n$ be a non-negative integer and $G$ an undirected graph. A path of length $n$ from $u$ to $v$ in $G$ is a sequence of $n$ edges $e_1,\dots ,e_n$ of $G$ for which there exists a sequence $x_0=u,x_1,\dots ,x_{n-1},x_n=v$ of vertices such that $e_i$ has, for $i=1,\dots ,n$, the endpoints $x_{i-1}$ and $x_i$. When the graph is simple, we denote this path by its vertex sequence $x_0,x_1,\dots ,x_n$ (because listing these vertices uniquely determines the path).

Tip

Here the length is the number of edges, i.e., the number of vertices minus one.

The path is a circuit if it begins and ends at the same vertex, that is, if $u=v$, and has length greater than zero. The path or circuit is said to pass through the vertices $x_1,x_2,\dots ,x_{n-1}$ or traverse the edges $e_1,e_2,\dots ,e_n$. Path or circuit is simple if it does not contain the same edge more than once.

Let $n$ be a nonnegative integer and $G$ a directed graph. A path of length $n$ from $u$ to $v$ in $G$ is a sequence of edges $e_1,e_2,\dots ,e_n$ of $G$ such that $e_1$ is associated with $(x_0,x_1)$, $e_2$ is associated with $(x_1,x_2)$, and so on, with $e_n$ associated with $(x_{n-1},x_n)$, where $x_0=u$ and $x_n=v$.

When there are no multiple edges in the directed graph, this path is denoted by its vertex sequence $x_0,x_1,x_2,\dots ,x_n$. A path of length greater than zero that begins and ends at the same vertex is called a circuit or cycle. A path or circuit is called simple if it does not contain the same edge more than once.

Connectedness in Undirected Graphs

An undirected graph is called connected if there is a path between every pair of distinct vertices of the graph. An undirected graph that is not connected is called disconnected. We say that we disconnect a graph when we remove vertices or edges, or both, to produce a disconnected subgraph.

There is a simple path between every pair of distinct vertices of a connected undirected graph.

A connected component of a graph $G$ is a connected subgraph of $G$ that is not a proper subgraph of another connected subgraph of $G$. That is, a connected component of a graph $G$ is a maximal connected subgraph of $G$. A graph $G$ that is not connected has two or more connected components that are disjoint and have $G$ as their union.

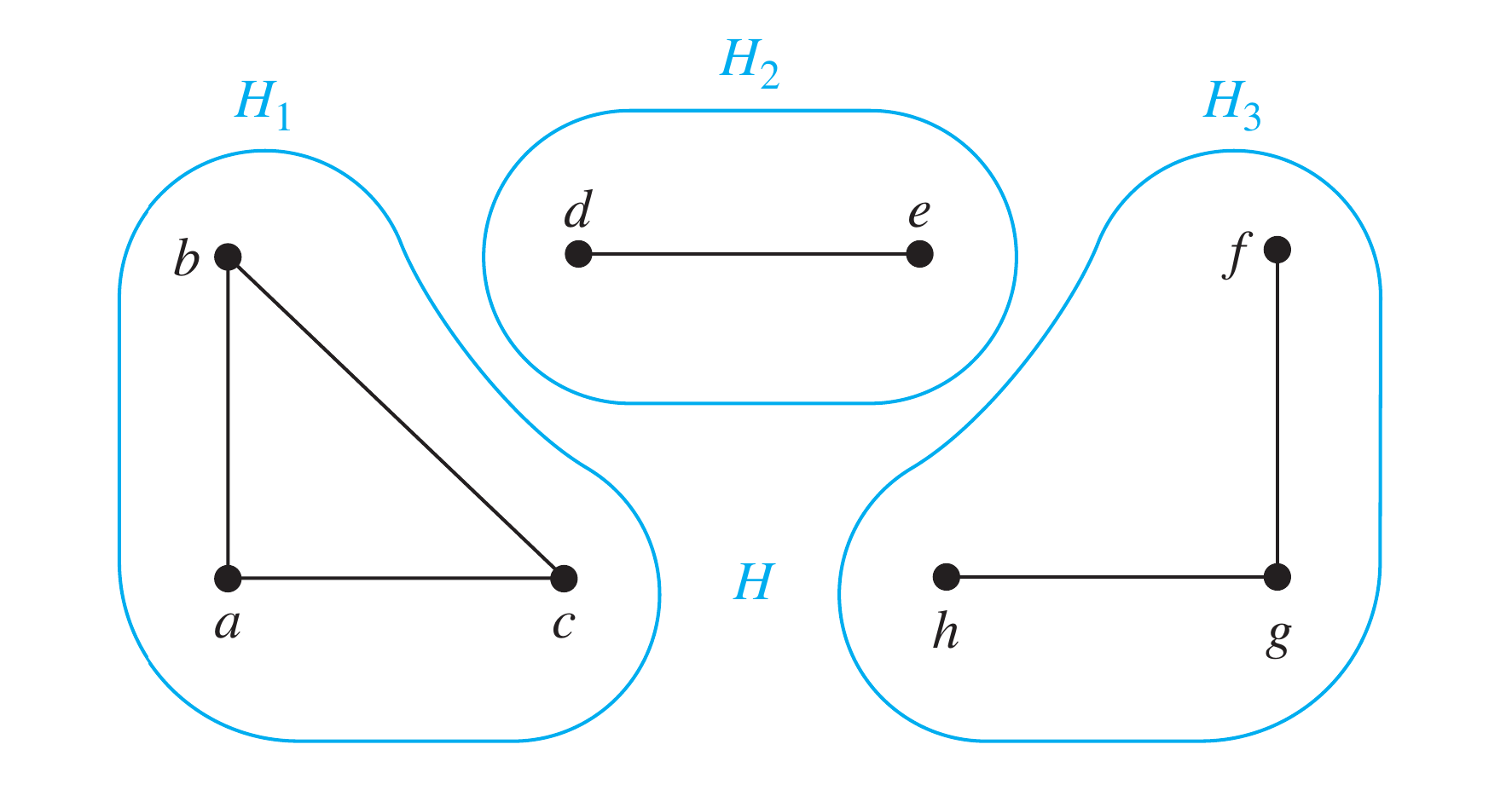
Note

An isolated vertex itself can be a connected component

Connectedness in Undirected Graphs

Cut Vertices and Cut Edges

Sometimes the removal from a graph of a vertex and all incident edges produces a subgraph with more connected components. Such vertices are called cut vertices (or articulation points). The removal of a cut vertex from a connected graph produces a subgraph that is not connected.

Analogously, an edge whose removal produces a graph with more connected components than in the original graph is called a cut edge or bridge. Note that in a graph representing a computer network, a cut vertex and a cut edge represent an essential router and an essential link that cannot fail for all computers to be able to communicate

Vertex Connectivity

A subset $V^{\prime }$ of the vertex set $V$ of $G=(V,E)$ is a vertex cut, or separating set, if $G-V^{\prime }$ is disconnected. We define the vertex connectivity of a non-complete graph $G$ (since complete graphs have no cut vertices), denoted by $\kappa (G)$, as the minimum number of vertices in a vertex cut, i.e., the the minimum number of vertex to remove in order to disconnect the graph.

The larger $\kappa (G)$ is, the more connected we consider $G$ to be. We say that a graph is $k$-connected if $\kappa (G)\ge k$. A graph G is $1$-connected if it is connected and not a graph containing a single vertex (otherwise we can not say that a graph with no vertices is disconnected); a graph is $2$-connected, or biconnected, if it is non-separable and has at least three vertices. Note that if $G$ is a $k$-connected graph, then $G$ is a $j$-connected graph for all $j$ with $0\le j\le k$.

Edge Connectivity

A set of edges $E^{\prime }$ is called an edge cut of $G$ is the subgraph $G-E^{\prime }$ is disconnected. The edge connectivity of a graph $G$, denoted by $\lambda (G)$, is the minimum number of edges in an edge cut of $G$. This defines $\lambda (G)$ for all connected graphs with more than one vertex because it is always possible to disconnect such a graph by removing all edges incident of one of its vertices.

Inequality for Vertex Connectivity and Edge Connectivity

$$\kappa (G)\le \lambda (G)\le \underset{v\in V}{\min }\mathrm{deg}(v)$$

Connectedness in Directed Graphs

A directed graph is strongly connected if there is a path from $a$ to $b$ and from $b$ to $a$ whenever $a$ and $b$ are vertices in the graph.

A directed graph is weakly connected if there is a path between every two vertices in the underlying undirected graph.

The subgraphs of a directed graph $G$ that are strongly connected but not contained in larger connected subgraphs, that is, the maximal strongly connected subgraphs, are called the strongly connected components or strong components of $G$. Note that if $a$ and $b$ are two vertices in a directed graph, their strong components are either the same or disjoint.

Counting Paths Between Vertices

Let $G$ be a graph with adjacency matrix$\text{A}$ with respect to the ordering $v_1,v_2,\dots ,v_n$ of the vertices of the graph (with directed or undirected edges, with multiple edges and loops allowed). The number of different paths of length $r$ from $v_i$ to $v_j$, where $r$ is a positive integer, equals the $(i,j)$-th entry of ${\text{A}}^r$