Graph

Definition

Basic Definition

A graph $G=(V,E)$ consists of $V$, a non-empty set of vertices (or nodes) and $E$, a set of edges. Each edge either one or two vertices associated with it, called its endpoints. An edge is said to connect its endpoints.

Basic Types

A undirected graph in which each edge connects two different vertices (i.e. no loops) and where no two edges connect the same pair of vertices is called a simple graph.

Graphs that may have multiple edges connecting the same vertices are called multigraphs.

Graphs that may include loops, and possibly multiple edges connecting the same pair of vertices or a vertex to itself, are sometimes called pseudographs.

Graph Terminology

Neighbors and Neighborhood (Undirected Graph)

Two vertices $u$ and $v$ in an undirected graph $G$ are called adjacent (or neighbors) in $G$ if $u$ and $v$ are endpoints of an edge $e$ of $G$. Such an edge $e$ is called incident with the vertices $u$ and $v$ and $e$ is said to connect $u$ and $v$.

The set of all neighbors of a vertex $v$ of $G=(V,E)$, denoted by $N(v)$, is called the neighborhood of $v$. If $A$ is a subset of $V$, we denoted by $N(A)$ the set of all vertices in $G$ that are adjacent to at least one vertex in $A$. So, $N(A)={\bigcup }_{v\in A}N(v)$.

Degree (Undirected Graph)

The degree of a vertex in an undirected graph is the number of edges incident with it, except that a loop at a vertex contributes twice to the degree of that vertex. The degree of the vertex $v$ is denoted by $\mathrm{deg}(v)$

A vertex of degree zero is called isolated. It follows that an isolated vertex is not adjacent to any vertex. A vertex is pendant if and only if it has degree one

The

Let $G=(V,E)$ be an undirected graph with $m$ edges. Then

$$2m=\sum _{v\in V}\mathrm{deg}(v)$$

(Note that this applies even if multiple edges and loops are present)

As a result of this theorem, an undirected graph has an even number of vertices of odd degree.

Adjacent (Directed Graph)

When $(u,v)$ is an edge of the graph $G$ with directed edges, $u$ is said to be adjacent to $v$ and $v$ is said to be adjacent from $u$. The vertex $u$ is called the initial vertex of $(u,v)$, and $v$ is called the terminal or end vertex of $(u,v)$. The initial and terminal vertex of a loop are the same.

Degree (Directed Graph)

In a graph with directed edges the in-degree of a vertex $v$, denoted by ${\mathrm{deg}}^{-}(v)$, is the number of edges with $v$ as their terminal vertex. The out-degree of $v$, denoted by ${\mathrm{deg}}^{+}(v)$, is the number of edges with $v$ as their initial vertex. Note that a loop at a vertex contributes 1 to both the in-degree and the out-degree of this vertex

Let $G=(V,E)$ be a graph with directed edges. Then

$$\sum _{v\in V}{\mathrm{deg}}^{-}(v)=\sum _{v\in V}{\mathrm{deg}}^{+}(v)=\left|E\right|$$

Some Special Simple Graphs

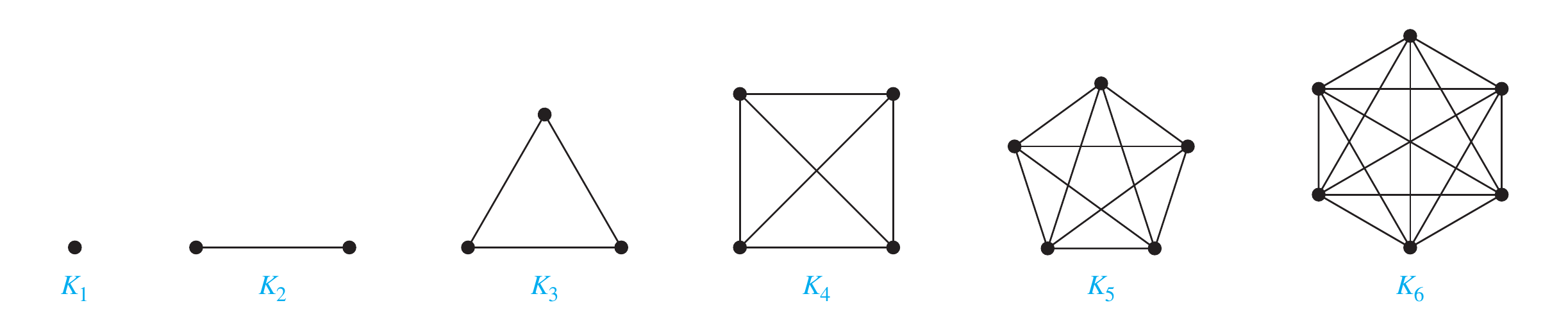
Complete Graphs

A complete graph on $n$ vertices, denoted by $K_n$, is a simple graph that contains exactly one edge between each pair of distinct vertices.

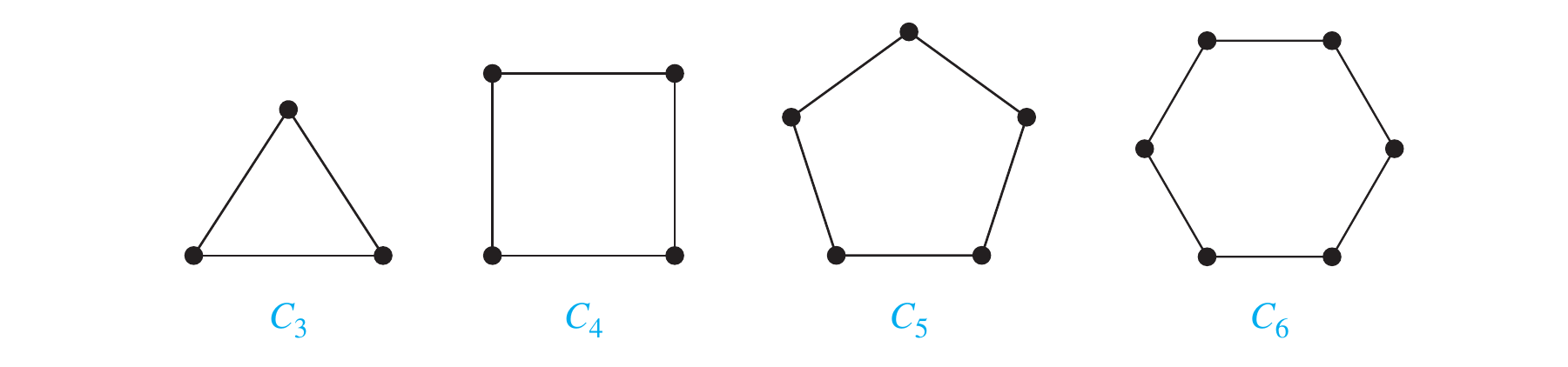
Cycles

A cycle $C_n$, $n\ge 3$, consists of $n$ vertices $v_1,v_2,\dots ,v_n$ and edges $\left\{v_1,v_2\right\},\left\{v_2,v_3\right\},\dots ,\left\{v_{n-1},v_n\right\}$ and $\left\{v_n,v_1\right\}$.

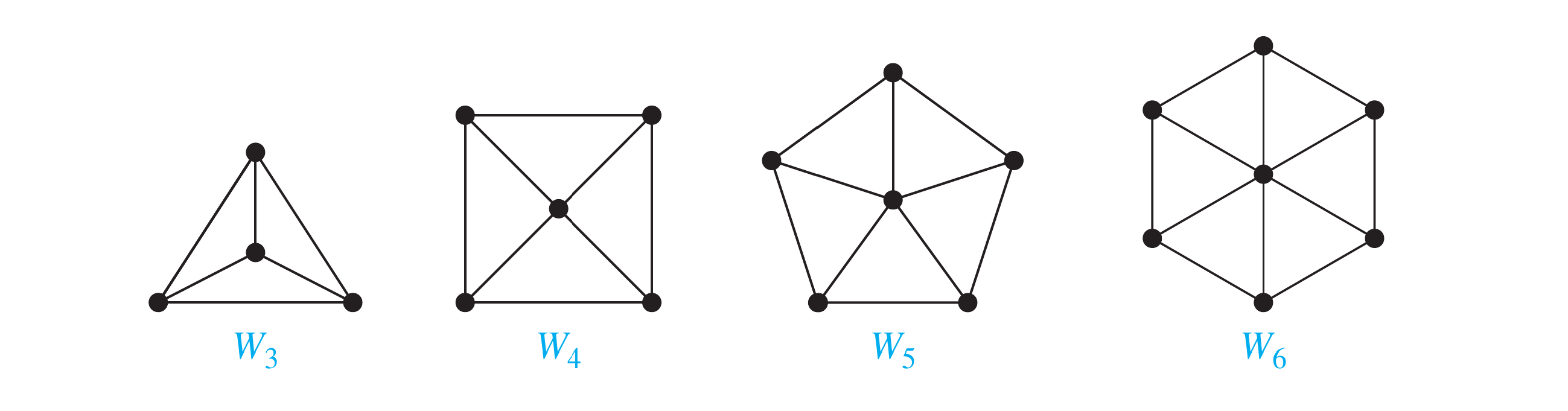
Wheels

We obtain a wheel $W_n$ when we add an additional vertex to a cycle $C_n$, for $n\ge 3$, and connect this new vertex to each of the $n$ vertices in $C_n$, by new edges.

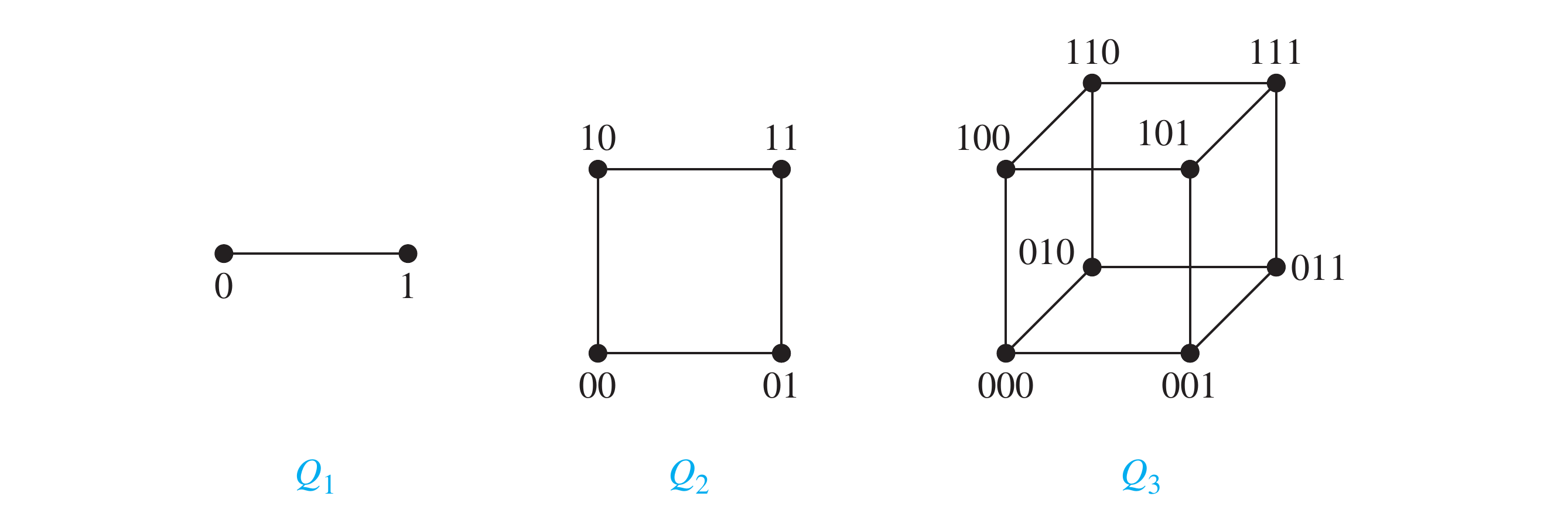
$n$-Cubes

An $n$-dimensional hypercube, or $n$-cube, denoted by $Q_n$, is a graph that has vertices representing the $2^n$ bit strings of length $n$. The vertices are adjacent if and only if the bit strings that they represent differ in exactly on bit position.

New Graphs from Old

Subgraph

A subgraph of a graph $G=(V,E)$ is a graph $H=(W,F)$, where $W\subseteq V$ and $F\subseteq E$. A subgraph $H$ of $G$ is a proper subgraph of $G$ if $H\ne G$.

Let $G=(V,E)$ be a simple graph. The subgraph induced by a subset $W$ of the vertex set $V$ is the graph $(W,F)$, where the edge set $F$ contains an edge in $E$ if and only if both endpoints of this edge are in $W$.

Graph Unions

The union of two simple graphs $G_1=(V_1,E_1)$ and $G_2=(V_2,E_2)$ is the simple graph with vertex set $V_1\cup V_2$ and edge set $E_1\cup E_2$. The union of $G_1$ and $G_2$ id denoted by $G_1\cup G_2$.

Representation

Representing Graphs

Adjacency Lists

Vertex	Adjacent Vertices
$a$	$b,c,e$
$b$	$a$
$c$	$a,d,e$
$d$	$c,e$
$e$	$a,c,d$

Adjacency Matrices

Suppose that $G=(V,E)$ is a simple graph where $\left|V\right|=n$. Suppose that the vertices of $G$ are listed arbitrarily as $v_1,v_2,\dots ,v_n$. The adjacency matrix $\text{A}$ of $G$, with respect to this listing of the vertices, is the $n\times n$ zero-one matrix $\text{A}=(a_{ij})$, such that

$$a_{ij}=\{\begin{array}{ll}1,& \text{if}\left\{v_i,v_j\right\}\text{is an edge of}G,\\ 0,& \text{otherwise}.\end{array}$$

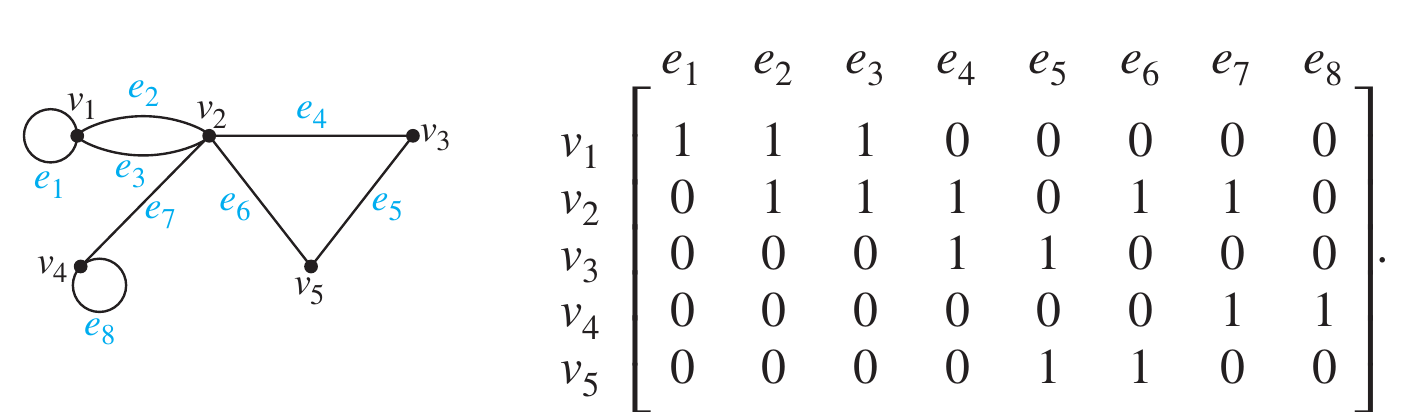
Incidence Matrices

Let $G=(V,E)$ be an undirected graph. Suppose that $v_1,\dots ,v_n$ are vertices and $e_1,\dots ,e_m$ are the edges of $G$. Then the incidence matrix with respect to this ordering of $V$ and $E$ is the $n\times m$ matrix $\text{M}=(m_{ij})$, where

$$m_{ij}=\{\begin{array}{ll}1,& \text{when edge}{e}_j\text{is incident with}{v}_i,\\ 0,& \text{otherwise}.\end{array}$$

Incidence matrices can also be used to represent multiple edges and loops. Multiple edges are represented in the incidence matrix using columns with identical entries, because these edges are incident with the same pair of vertices. Loops are represented using a column with exactly one entry equal to $1$, corresponding to the vertex that is incident with this loop.