Crystal Polarization Optics

双折射

取一块冰洲石（方解石的一种, 主要成分是$\mathrm{CaC}{\mathrm{O}}_3$）, 放在一张有字的纸上, 我们将看到双重影像 这表明, 光在这种晶体内形成了两束, 它们的折射程度不同, 这种现象叫做双折射

o光和e光

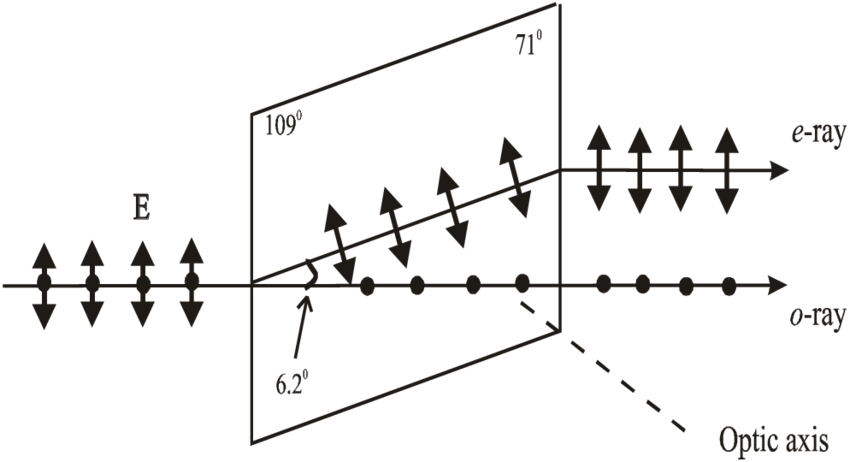让一束平行的自然光正入射在冰洲石晶体的一个表面上, 我们就会发现光束分解成两束, 其中一束光遵循折射定律, 称为寻常光(ordinary ray, o光), 另一束会违背它, 称为非常光(extraordinary ray, e光). 应当注意, o光和e光只有在双折射晶体内部有意义, 射出晶体后就无所谓o光和e光了

晶体的光轴

在冰洲石中存在一个特殊的方向, 光线沿着这个方向传播时o光和e光不分开（即它们的传播速度和传播方向都一样）, 这个特殊的方向（不是一条特殊的线）称为晶体的光轴.

主截面

当光线沿着晶体的某个界面入射时, 此界面的法线和晶体的光轴组成的平面称为主截面. 只有入射线在主截面内, 也就是入射面与主截面重合时, 才能保证e光也在入射面内

双折射光的偏振

o光和e光都是线偏振光, 且它们的振动方向相互垂直

单轴晶体中的波面

双折射晶体分为两类, 只有一个光轴方向的称为单轴晶体；有两个光轴方向的称为双轴晶体

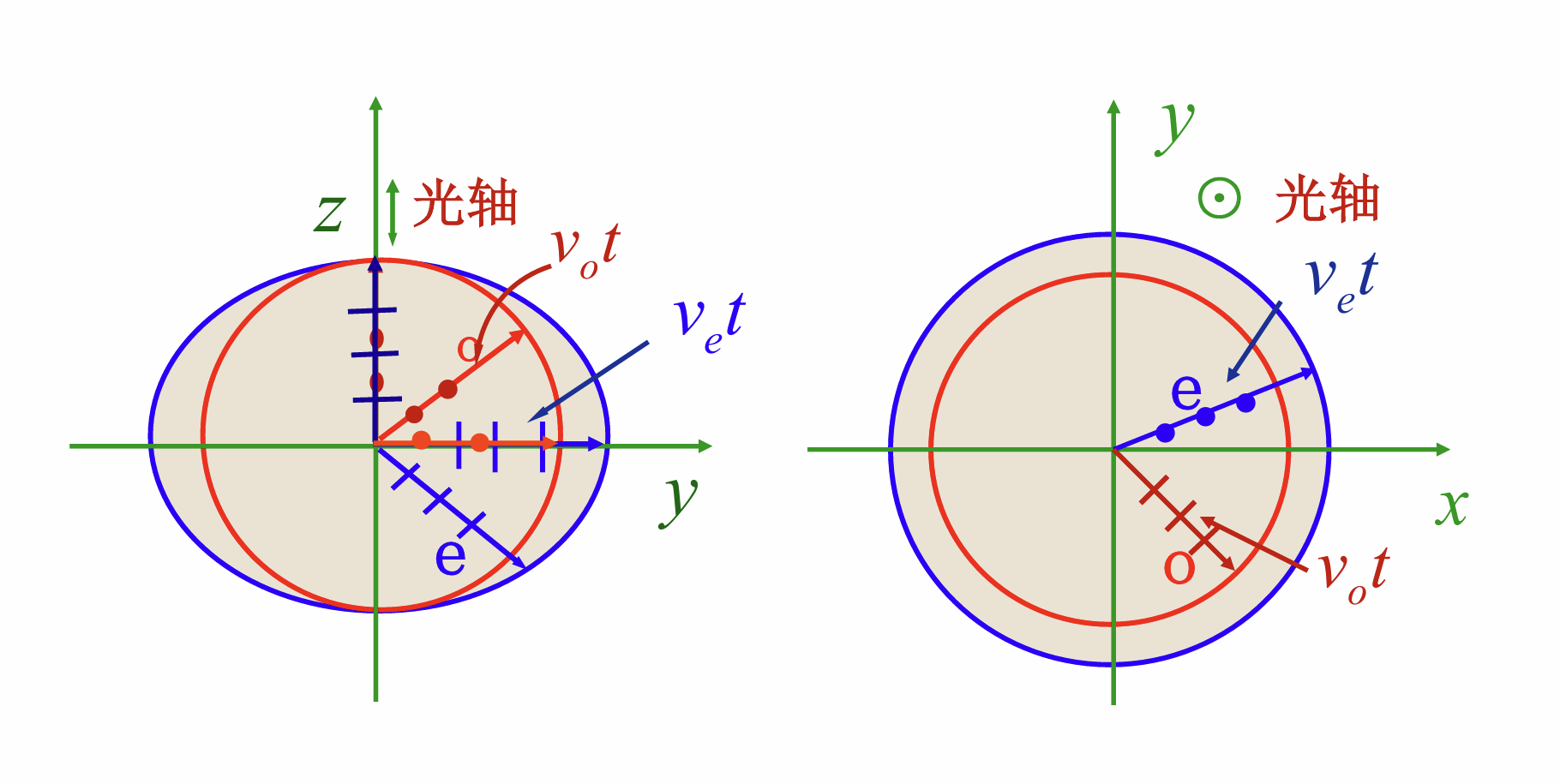
我们知道, 在各向同性介质中的一个点光源发出的波沿各个方向的传播速度都是$v=\frac{c}{n}$, 经过某段时间$\Delta t$后形成的波面是一个半径为$v\Delta t$的球面

在单轴晶体中的o光传播规律与普通各向同性介质中意义, 其波面也是球面. 但是e光沿各个方向的传播速度不同, 沿光轴方向的速度和o光一样, 也就是$v_o$. 垂直光轴方向的传播速度是另一个数值$v_e$. 在经过$\Delta t$时间后e光的波面就是一个椭球. 把两个波面画在一起, 它们在光轴方向上相切.

为了说明o光和e光的偏振方向, 我们引入主平面的概念. 晶体中某条光线与晶体光轴构成的平面叫做主平面, 下面左边图中的纸面就是图中所画光线的主平面 o光电矢量的振动方向和主平面垂直, e光电矢量的振动方向和主平面平行, 故若入射光是振动方向和主平面夹角为$\theta$的、振幅为$A$的线偏振光, 那么它的振动矢量就可以分解为两个方向

$$A_e=A\cos \theta ,A_o=A\sin \theta$$

Tip

需要注意的是, 如果要求光强, 则和折射率有关 $I_o=n_o{A}_o^2,I_e=n_e(\varphi )A_e^2$ 其中$n_e$和入射光和光轴的夹角$\varphi$有关

单轴晶体分为两类: 一类以冰洲石为代表, $v_e>v_o$, 称为负晶体；另一类以石英为代表, $v_o>v_e$, 称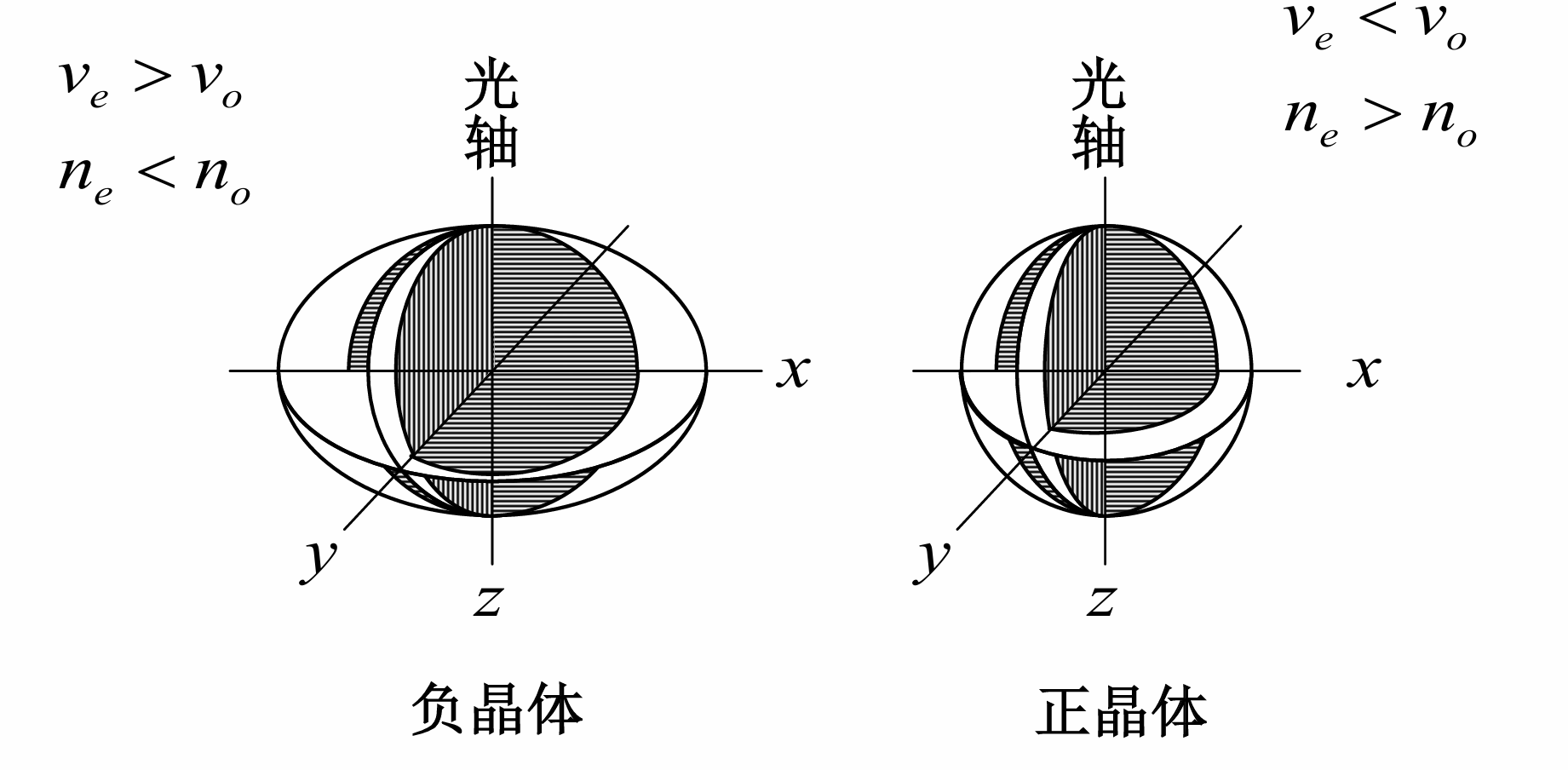为正晶体 对于e光, 由于它不符合普通的折射定律, 所以我们不能用一个简单的折射率来反映它的折射规律. 但是我们通常仍然把真空光速和e光沿垂直于光轴传播时候的速度之比叫做它的折射率$n_e=\frac{c}{v_e}$. 这个$n_e$虽然不具备普通折射率的含义, 但它和$n_o$一样都是晶体的一个重要光学参量, 我们称它们为晶体的主折射率

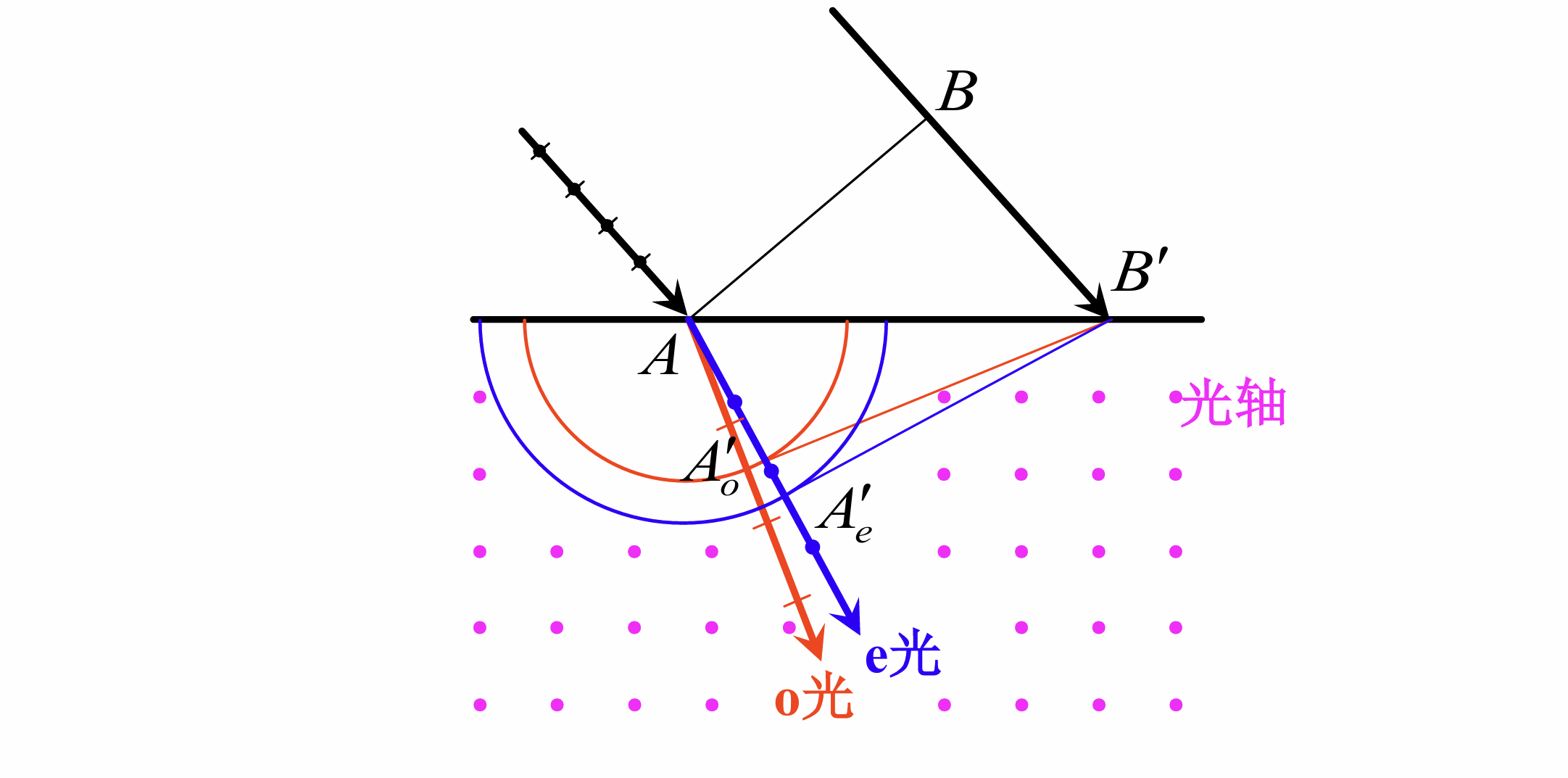
晶体的Huggens作图法

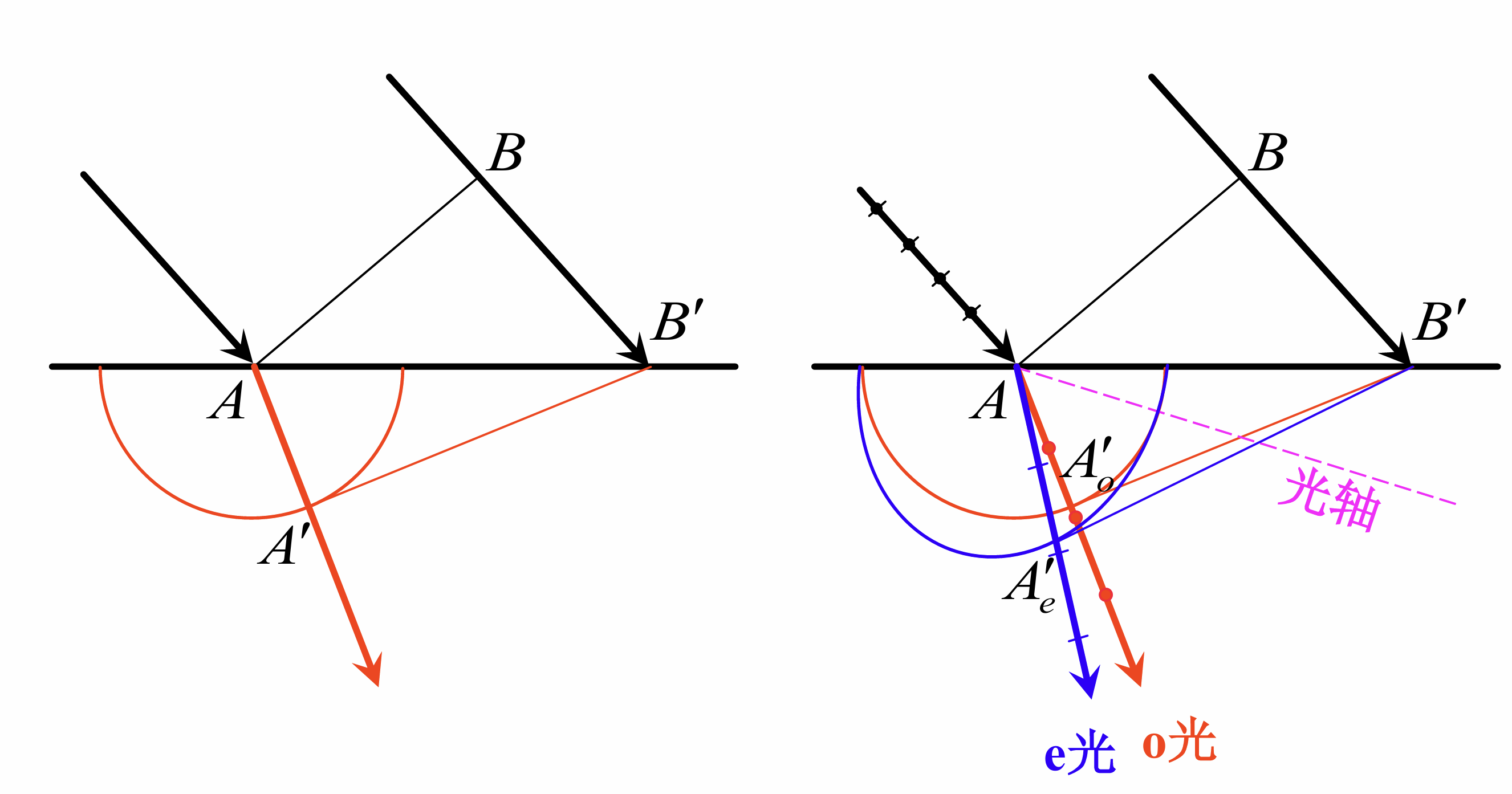具体步骤为

1. 画出平行的入射光束, 令两边缘光线和界面的交点为$A,B^{\prime }$
2. 由先到界面的$A$点作另一边边缘入射线的垂线$AB$, 它便是入射光的波面, 求出$B$到$B^{\prime }$的时间$t=\frac{\overline{B{B}^{\prime }}}{c}$
3. 以$A$为中心, $vt$为半径在折射介质内作半圆, 这就是另一边缘入射线到达$B^{\prime }$点时由$A$点发出的次波面；同时作以$A$为中心, 和半圆在光轴方向相切, 且另一半主轴长为$v_{e}t$的一个半椭圆
4. 通过$B^{\prime }$点作上述半圆的切线, 这就是o光的波面；作上述半椭圆面的切线, 这就是e光的波面

几个重要的特例

光轴垂直于界面, 正入射

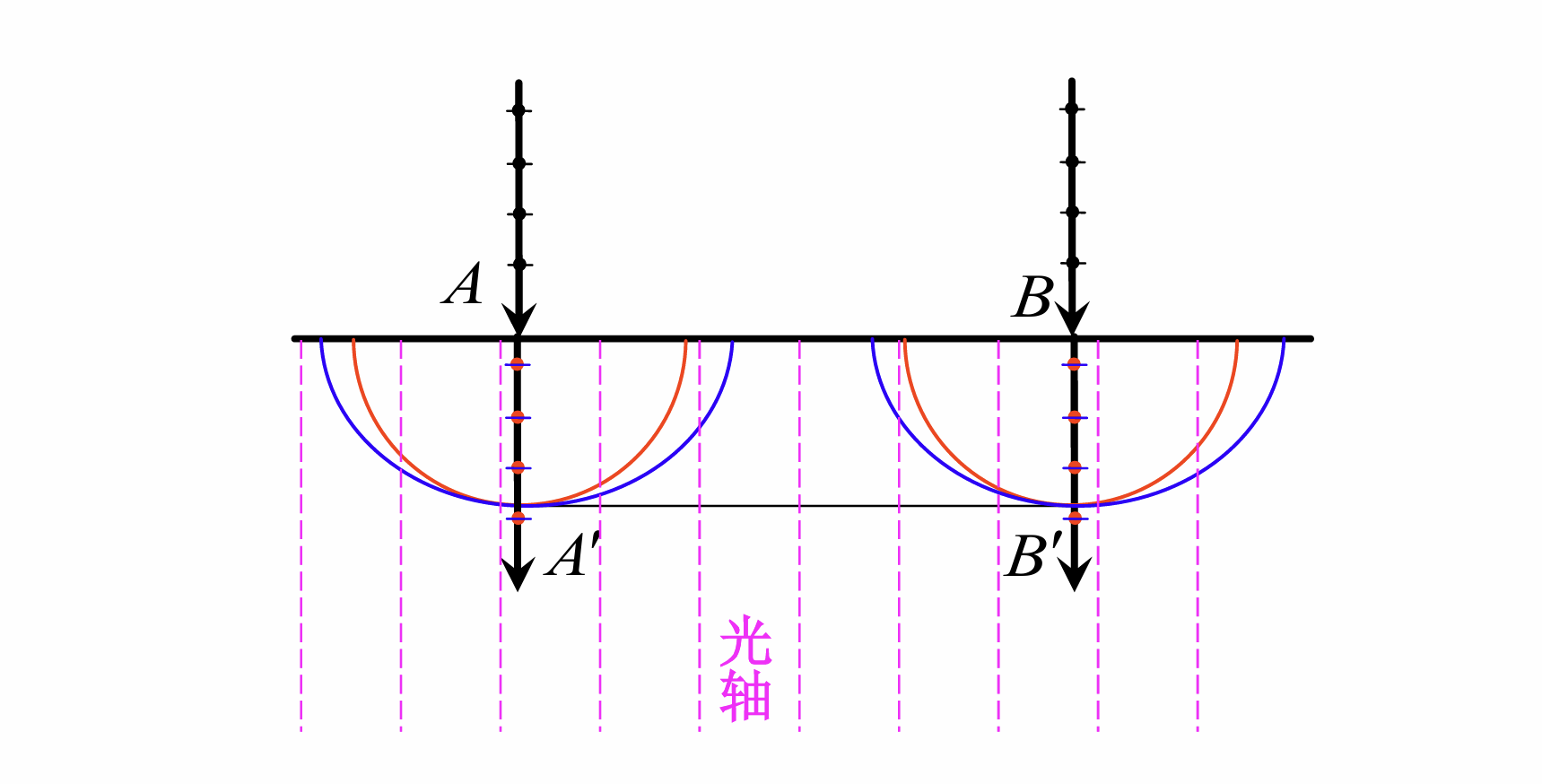
光轴平行于界面, 正入射

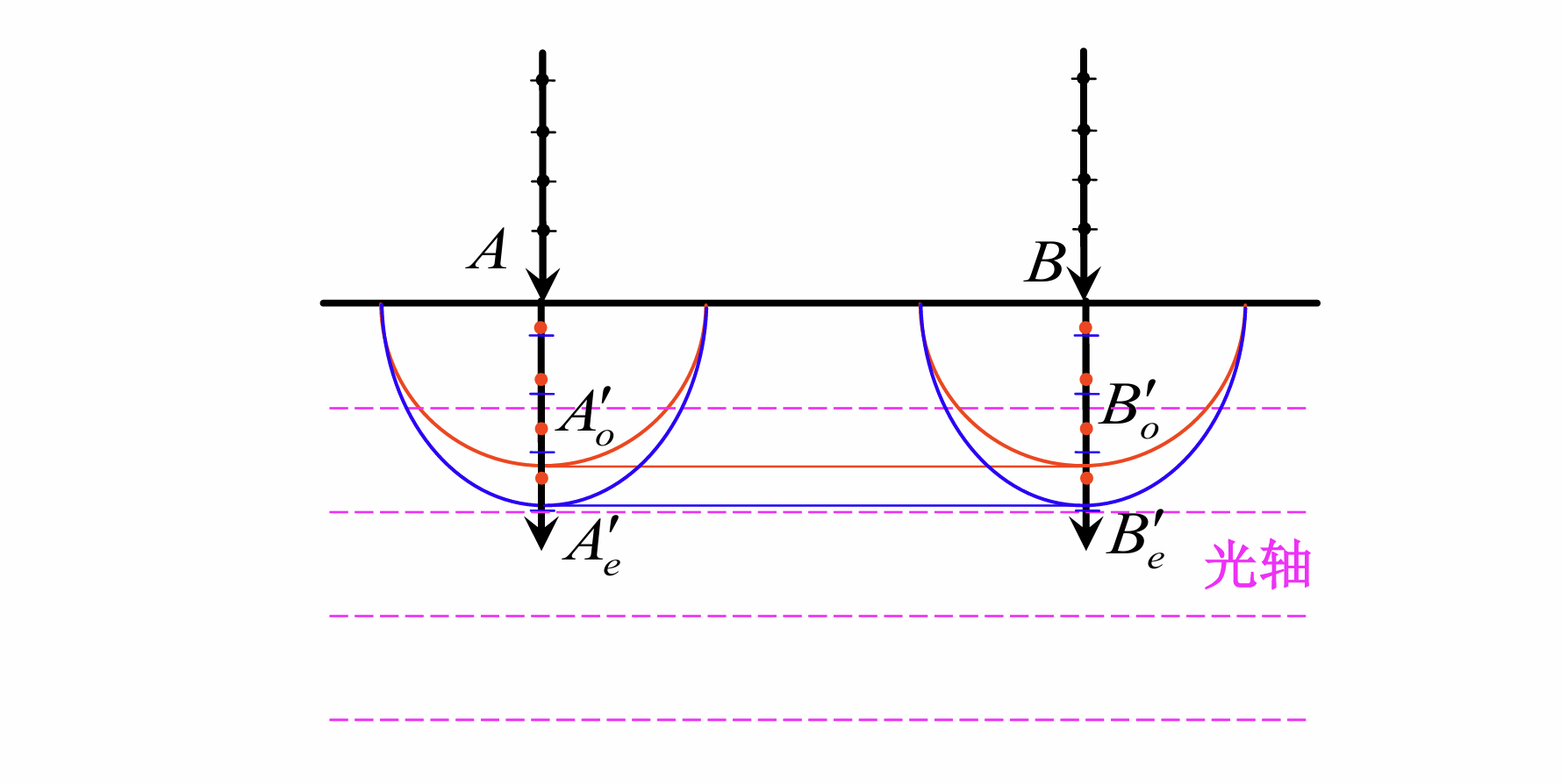
光轴垂直于界面, 正入射

此时有

$$n\sin \theta =n_o\sin {\theta }_o=n_e\sin {\theta }_e$$

晶体光学器件

晶体偏振器

利用双折射将两种偏振分开

Rochon棱镜

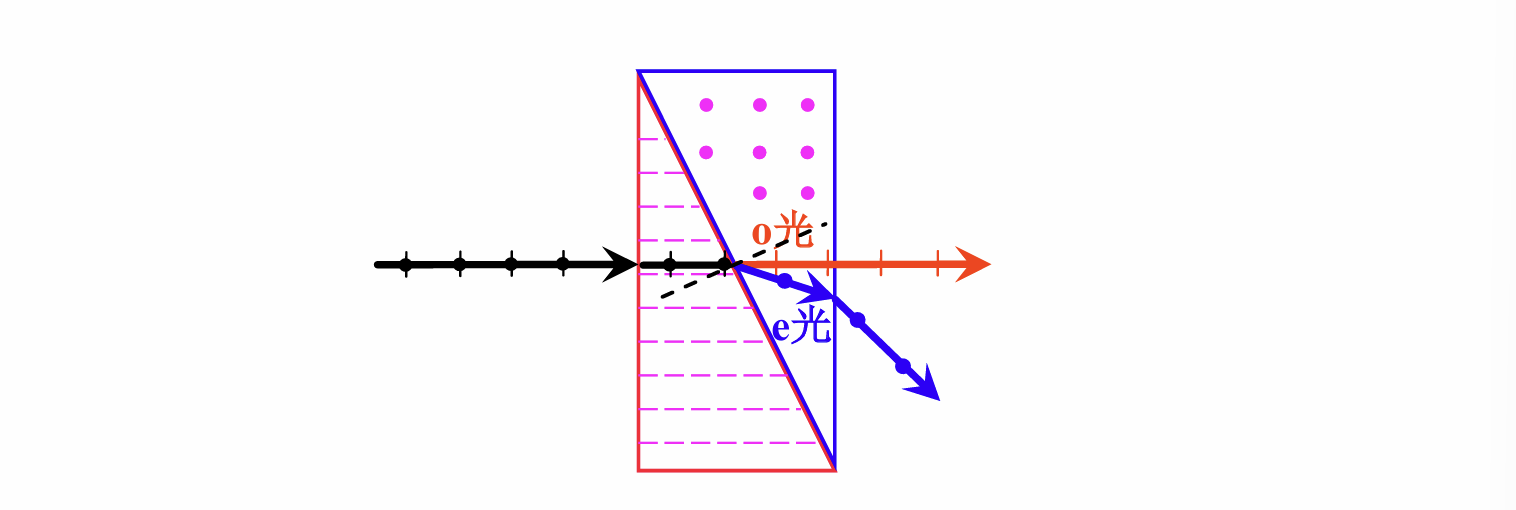对角面两边是同一种双折射介质, 但是光轴的方向相互垂直；自然光入射, 进入左边的棱镜后由于传播方向和光轴平行, 故各方向的振动分量的折射率均为$n_o$. 越过对角面后, 平行于纸面的分量垂直于新的主平面, 故其折射率仍然为$n_o$, 从而不发生不折射, 成为继续传播的o光；而垂直于纸面的分量则平行于新的主平面, 其折射率变为$n_e$, 故发生折射形成e光

Wollaston棱镜

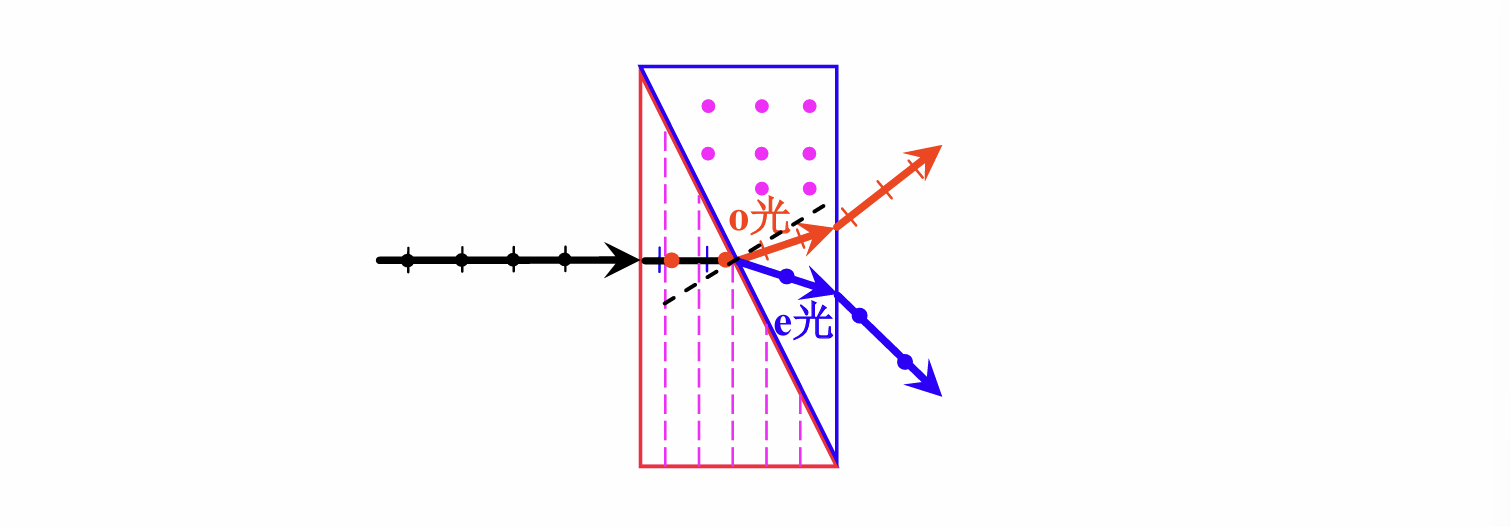对角面两边是同一种双折射介质, 但是光轴的方向相互垂直；入射, 进入左边的棱镜后由于传播方向和光轴垂直, 平行于纸面的振动分量的折射率为$n_e$, 垂直于纸面的振动分量的折射率为$n_o$. 越过对角面后, 平行于纸面的分量垂直于新的主平面, 其折射率变为为$n_o$, 故发生折射形成o光；而垂直于纸面的分量则平行于新的主平面, 其折射率变为$n_e$, 故发生折射形成e光

Nicol棱镜

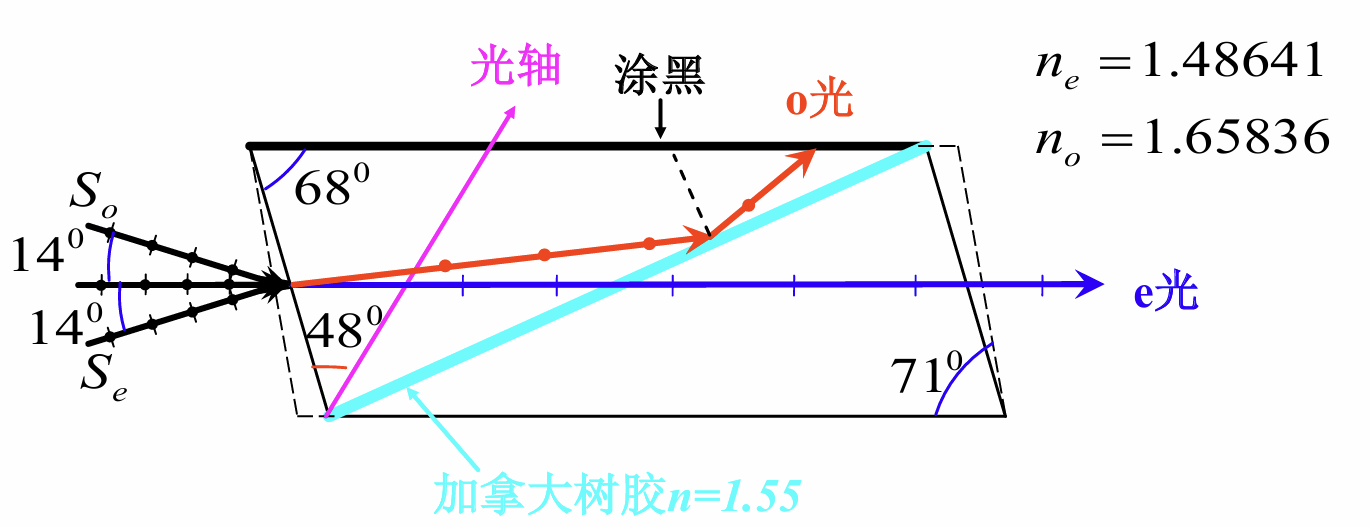其中o光在加拿大树胶面上恰好发生全发射, 从而偏离光路；而e光则保持传播路径, 最后射出. Nicol棱镜常被用来得到线偏振光

圆偏振光和椭圆偏振光的获得和检验

垂直振动的合成

$$\{\begin{array}{l}{E}_x=A_x\cos \omega t\\ E_y=A_y\cos (\omega t+\delta )\end{array}$$

1. $\delta =0,\pi$ 为线偏振光
2. $\delta =\pm \frac{\pi }{2}⟹\frac{E_x^2}{A_x^2}+\frac{E_y^2}{A_y^2}=1$; $\delta =\frac{\pi }{2}$为右旋, $\delta =-\frac{\pi }{2}$为左旋, 为正椭圆偏振光
3. 一般情况

$$\frac{E_x^2}{A_x^2}+\frac{E_y^2}{A_y^2}-\frac{2E_x{E}_y}{A_x{A}_y}\cos \delta ={\sin }^2\delta$$

此时$-\pi <\delta <0$为左旋, $0<\delta <\pi$为右旋, 为斜椭圆

自然光经过波晶片

• 自然光可正交分解, 每一个分量都含有相位随机的多列波, 在晶体中分为相互正交的o光、e光
• 经过波片后, 每一个分量仍然是相位随机的多列波 . 所以, 正交分量合成后, 仍是自然光
• 不考虑波片的吸收, 光强不变

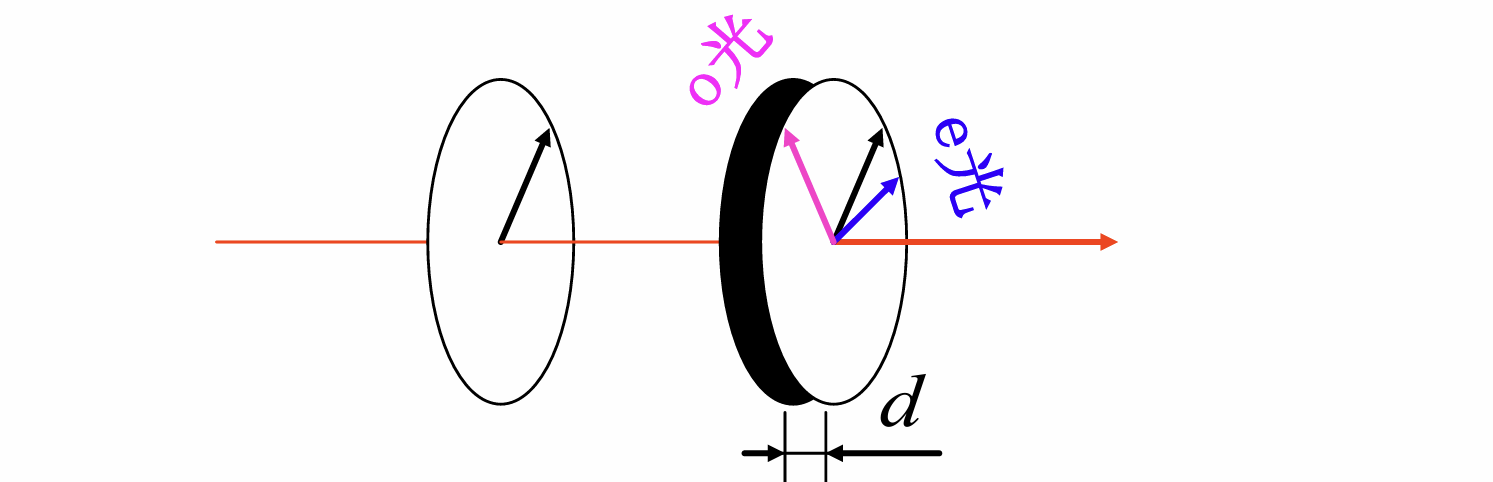
线（平面）偏振光经波晶片

在波片中分为正交的e光、o光, 它们在晶体内传播速度不同, 穿过晶片时产生一定附加的相位$\delta$. 射出晶片后两光束的速度恢复到一样, 合成在一起一般得到椭圆偏振光. 其中

$$\delta =\frac{2\pi }{\lambda }(n_o-n_e)d$$

要获得圆偏振光需要

1. $\delta =\pm \frac{\pi }{2}$, 厚度满足这一点的波片被称为四分之一波片
2. $A_e=A_0$, 设入射的线偏振光的振幅为$A$, 其振动方向与e轴的夹角为$\alpha$, 则必须有$\alpha =\frac{\pi }{4}$ 由此可以获得圆偏振光和椭圆偏振光

圆偏振光通过1/4波片

入射光的两正交分量间相位差为$\pm \frac{\pi }{2}$, 经过1/4波片后产生$\pm \frac{\pi }{2}$的额外相位差, 故出射光正交分量间的相位差是$0,\pi$, 故变为线偏振光, 电矢量和光轴成$45^{\circ }$角

椭圆偏振光通过1/4波片

斜椭圆偏振光通过后仍然是斜椭圆偏振光 正椭圆偏振光（椭圆长短轴和光轴重合）, 入射光的两正交分量间相位差为$\pm \frac{\pi }{2}$, 故出射光也是线/平面偏振光

圆偏振光和椭圆偏振光的检验

1. 使用线验偏器

旋转检偏器, 观察透射光强度的变化

• 自然光: 光强不变
• 圆偏振光: 光强不变
• 线偏振光: 光强改变, 在某一角度消光
• 部分偏振光: 光强改变, 但不消光
• 椭圆偏振光: 光强改变, 但不消光

2. 通过1/4波片

• 自然光: 仍是自然光
• 圆偏振光: 变为线偏振光
• 部分偏振光: 仍是部分偏振光
• 椭圆偏振光: 仍是椭圆偏振光, 当光轴与椭圆长短轴重合, 可以得到平面偏振光
• 再通过线检偏器, 可以将自然光与圆偏振 光鉴别；部分偏振光与椭圆偏振光鉴别

旋光

如果将一束线偏振光射入石英片, 那么出射的光也是线偏振光, 但是其振动面向左或向右旋转了一个角度$\psi$, 这种现象叫做旋光

实验表明, 振动面旋转角度$\psi$与石英晶片的厚度$d$成正比

$$\psi =\alpha d$$

比例系数$\alpha$叫做石英的旋光率, 旋光率的数值因波长而异, 因此在白光照射下, 不同颜色的振动面旋转的角度不同, 所以在石英片后放上偏振片, 将观察到色彩的变换, 这种现象叫做旋光色散

石英晶体有左旋和右旋两种变体, 它们的外形完全相似, 只是一种是另一种的镜像反演, 两种晶体使振动面的旋转方向相反

为了解释旋光性, Fresnel作出了如下假设: 在旋光晶体中线偏振光沿光轴传播时分解为左旋和右旋圆偏振光（L光和R光）, 它们的传播速度$v_L,v_R$略有不同, 或者说二者的折射率$n_L=\frac{c}{v_L},n_R=\frac{c}{v_R}$不同, 从而经过旋光晶片时产生不同的相位滞后

$${\varphi }_L=k\Delta L_L=\frac{2\pi }{\lambda }{n}_{L}d,{\varphi }_R=k\Delta L_R=\frac{2\pi }{\lambda }{n}_{R}d$$

假设沿$x$方向振动的线偏振光可以分解为如下的左旋圆偏振光和右旋圆偏振光

$$L:\{\begin{array}{l}{E}_x=A\cos (\omega t)\\ E_y=A\cos (\omega t-\frac{\pi }{2})\end{array}R:\{\begin{array}{l}{E}_x=A\cos (\omega t)\\ E_y=A\cos (\omega t+\frac{\pi }{2})\end{array}$$

它们的合成是$E_x=2A\cos (\omega ),E_y=0$, 而经过波片后有

$$L^{\prime }:\{\begin{array}{l}{E}_x=A\cos (\omega t+{\varphi }_L)\\ E_y=A\cos (\omega t-\frac{\pi }{2}+{\varphi }_L)\end{array}{R}^{\prime }:\{\begin{array}{l}{E}_x=A\cos (\omega t+{\varphi }_R)\\ E_y=A\cos (\omega t+\frac{\pi }{2}+{\varphi }_R)\end{array}$$

合成后变为

$$\{\begin{array}{l}{E}_x=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\cos \left(\frac{{\varphi }_L-{\varphi }_R}{2}\right)\\ E_y=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\cos \left(\frac{{\varphi }_L-{\varphi }_R-\pi }{2}\right)\end{array}$$

也就是

$$\{\begin{array}{l}{E}_x=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\cos \left(\frac{{\varphi }_L-{\varphi }_R}{2}\right)\\ E_y=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\sin \left(\frac{{\varphi }_L-{\varphi }_R}{2}\right)\end{array}$$

所以最后合成的线偏振光的方向和原来就偏离了一个角度

$$\psi =\frac{1}{2}({\varphi }_L-{\varphi }_R)=\frac{\pi }{\lambda }(n_L-n_R)d$$

因为把$x-y$坐标系逆时针旋转$\psi$角度后, 就有$E_x=2A\left(\omega t+{\phi }_0\right),E_y=0$