Neural Discrete Representation Learning

Auto-Encoder and Variational Auto-Encoder

Auto-Encoder (AE) is a type of neural network model that can compress images into shorter vectors (in latent space). The decoder of an AE can be seen as a image generator. However, the latent space of an AE is uneven, that is to say, the decoder only recognizes the vectors compiled by the encoder, but not the other vectors. If you input your own randomly generated vectors to the decoder, the decoder will not be able to generate a meaningful picture. Therefore, AE can only play the role of compressing the image.

Then, Variational Auto-Encoder (VAE) is proposed to solve the problem. It encodes the input image into a standard distribution, such as Gaussian, which allows it to generate realistic images by randomly sampling from the latent space.

However, the images generated by VAE are not very nice. The authors of VQ-VAE believe that the reason why VAE's generated images are not of high quality is that the images are encoded as continuous vectors. In fact, it would be more natural to encode the images as discrete vectors.

VQ-VAE

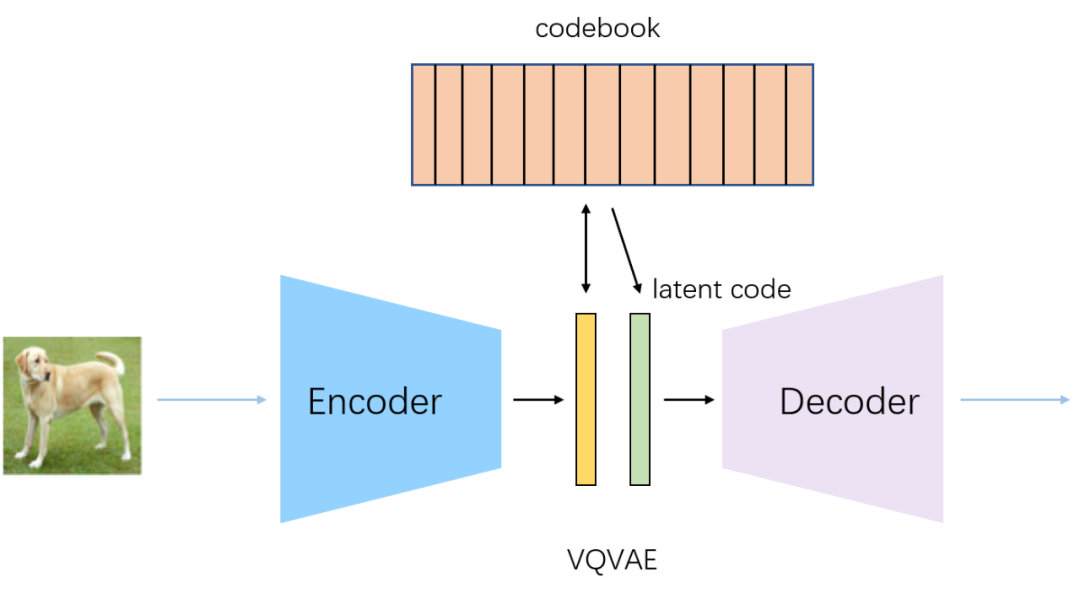We have two issues to encode the image into discrete vectors.

The first problem is that neural networks typically assume the input follows a continuous distribution, making them less effective at handling discrete inputs. If you directly input numbers like $0$, $1$, or $2$, the neural network might assume that $1$ is a state between $0$ and $2$. To solve this issue, we can borrow methods from word embeddings in NLP, where each input word is mapped to a unique continuous vector. In this way, each discrete number is transformed into a specific continuous vector.

We can add a similar embedding layer before the decoder in VQ-VAE. This embedding layer is referred to as the "embedding space" in VQ-VAE and is later called the "codebook" in subsequent articles.

Another issue with discrete vectors is that they are difficult to sample. Recall that the reason VAE encodes images into continuous vectors that follow a Gaussian distribution is to enable image generation by discarding the encoder, allowing randomly sampled vectors to be decoded into images. Now, with VQ-VAE encoding images into discrete vectors, the space formed by these discrete vectors is difficult to sample from.

The VQ-VAE itself is not an image generation model. Like AE, it is good at compressing images, reducing them into much shorter vectors, but it does not support random image generation. The only difference between VQ-VAE and AE is that VQ-VAE encodes discrete vectors, while AE encodes continuous vectors.

Pixel-CNN

To solve the second problem, the authors of VQ-VAE designed an image generation network called Pixel-CNN. Pixel-CNN can fit a discrete distribution. For example, for an image, Pixel-CNN can output the probability distribution of a particular color channel of a pixel taking on a value between $0$ and $255$.

This is how the whole model works:

1. Train the encoder and decoder of VQ-VAE so that it can convert an image into a "small image" and back into a full image.
2. Train Pixel-CNN to learn how to generate these "small images."
3. During random sampling, first use Pixel-CNN to sample a "small image," then use VQ-VAE to translate the "small image" into the final generated image.

Model Details

How to Get Discrete Embeddings

For each output vector of the encoder $z_{\mathrm{e}}(x)$, find it nearest neighbor $z_{\mathrm{q}}(x)$ in the trained embedding space, then replace $z_{\mathrm{e}}(x)$ by $z_{\mathrm{q}}(x)$ as the final output of the encoder.

Stop Gradient

We view VQ-VAE as a AE, and the loss function is the reconstruction function

$$L_{\text{reconstruction}}=\Vert x-\mathrm{decoder}(z_q(x)){\Vert }^2$$

However, we can not calculate the gradient of the step $z_{\mathrm{e}}(x)\to z_{\mathrm{q}}(x)$. To solve this, VQ-VAE proposes a stop gradient operation

$$\mathrm{sg}(x)=\{\begin{array}{ll}x,& \text{in forward propagation}\\ 0,& \text{in backward propagation}\end{array}$$

And now we can design

$$L_{\text{reconstruction}}=\Vert x-\mathrm{decoder}\left[z_{\mathrm{e}}(x)+\mathrm{sg}(z_{\mathrm{q}}(x)-z_{\mathrm{e}}(x))\right]{\Vert }^2$$

That is

$$L_{\text{reconstruction}}=\{\begin{array}{ll}\Vert x-\mathrm{decoder}(z_{\mathrm{q}}(x)){\Vert }^2,& \text{in forward propagation}\\ \Vert x-\mathrm{decoder}(z_{\mathrm{e}}(x)){\Vert }^2,& \text{in backward propagation}\end{array}$$

Therefore we can pass the gradient to $z_{\mathrm{e}}$ in back-propagation.

Train the Embedding Space

So far, our discussion has been based on the assumption that the embedding space has already been trained. Now, let's talk about how the embedding space is trained. Each vector in the embedding space should summarize a class of vectors output by the encoder. For example, a vector representing "youth" should summarize all encoder outputs for photos of people aged 14 to 35. Therefore, the vectors in the embedding space should be as close as possible to their corresponding encoder outputs, so we get

$$L_{\mathrm{embedding}}=\Vert z_{\mathrm{e}}(x)-z_{\mathrm{q}}(x){\Vert }^2$$

However, the author believes that the learning rates of the encoder and the embedding vectors should differ. Therefore, they used the stop gradient technique again to break the error function mentioned above into two parts.

$$L_{\mathrm{embedding}}=\Vert \mathrm{sg}(z_{\mathrm{e}}(x))-z_{\mathrm{q}}(x){\Vert }^2+\beta \Vert z_{\mathrm{e}}(x)-\mathrm{sg}(z_{\mathrm{q}}(x))\Vert$$

where the first term optimize the embedding space (refer Vector Quantization, the VQ in VQ-VAE), and the second term optimize the encoder. $\beta$ is introduced to control the relative learning rate.