Variational Auto-Encoder (VAE)

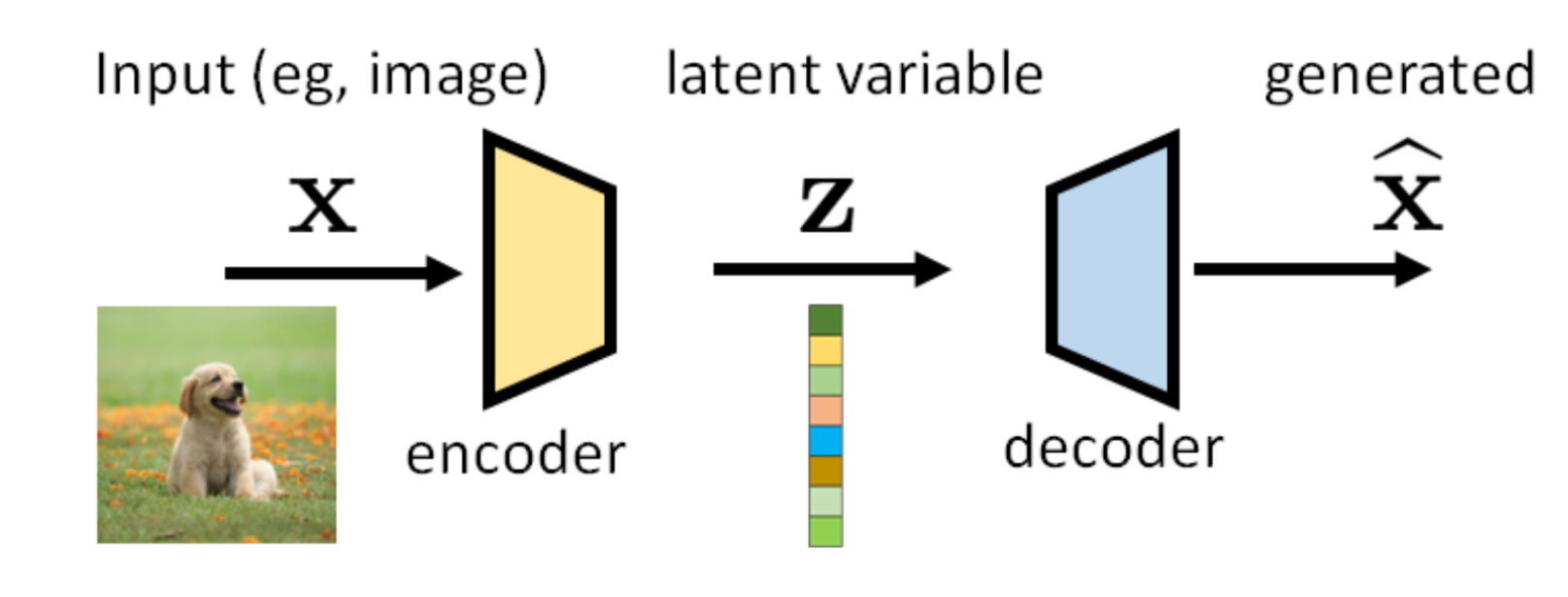
Model

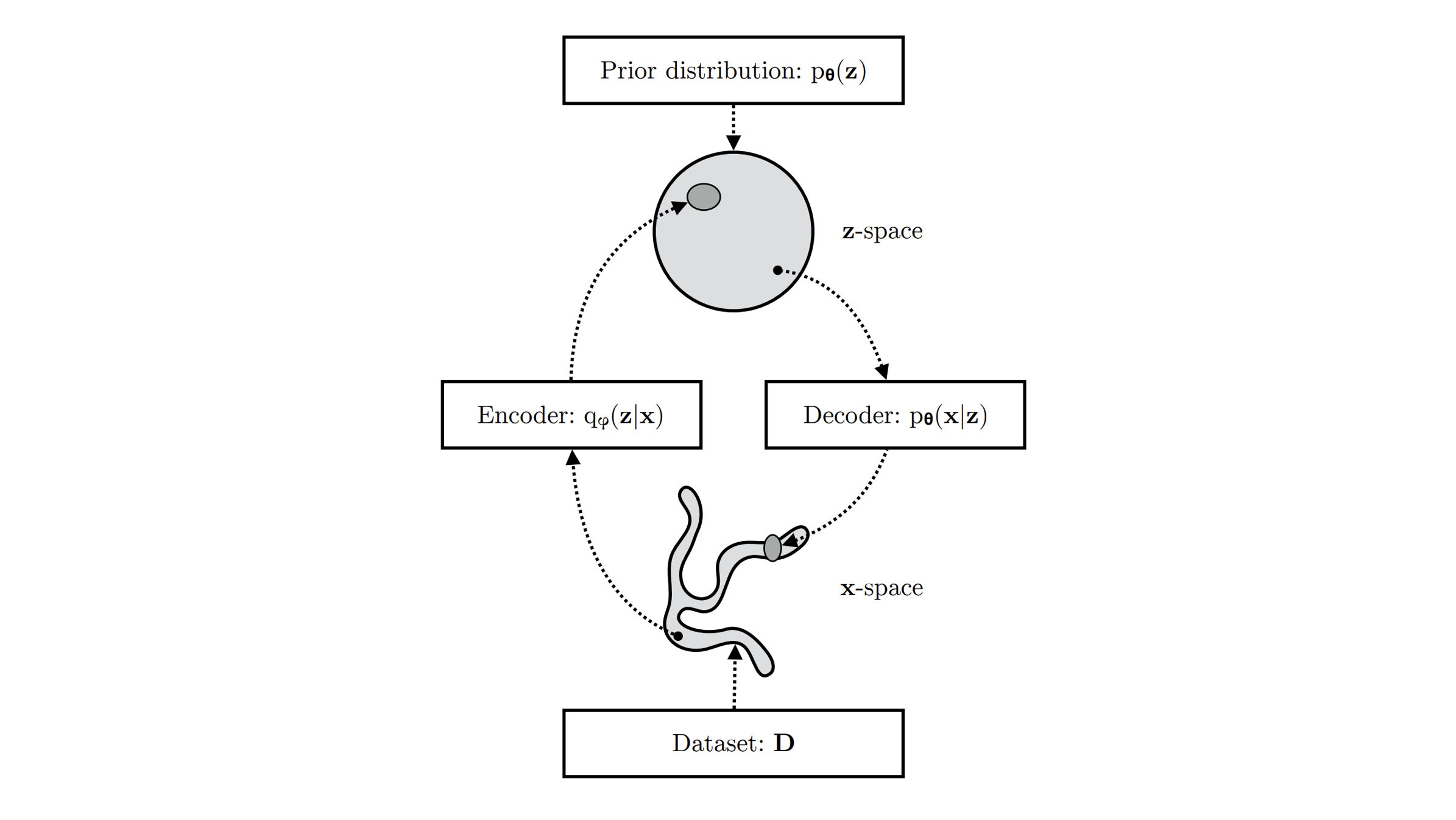
A variational auto-encoder (VAE) is an approach to generate images from a latent code. The name “variational” comes from the factor that we use probability distributions to describe $\mathbf{x}$ and $\mathbf{z}$. Instead of resorting to a deterministic procedure of converting $\mathbf{x}$ to $\mathbf{z}$, we are more interested in ensuring that the distribution $p(\mathbf{x})$ can be mapped to a desired distribution $p(\mathbf{z})$, and go backwards to $p(\mathbf{x})$. Since it's hard to directly access $p(\mathbf{z}|\mathbf{x})$ (the decoder) and $p(\mathbf{x}|\mathbf{z})$ (the encoder), we consider the following two proxy distributions to approximate them:

• $q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$: The proxy for $p(\mathbf{z}|\mathbf{x})$ with learnable parameter $\mathbf{\varphi }$. We will make it Gaussian to simplify the computation
• $p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})$: The proxy for $p(\mathbf{x}|\mathbf{z})$ with learnable parameter $\mathbf{\theta }$. We will also make it Gaussian to simplify the computation So the whole procedure of VAE can be

$$\mathbf{x}\stackrel{p(\mathbf{z}|\mathbf{x})\approx q_{\varphi }(\mathbf{z}|\mathbf{x})}{\to }\mathbf{z}\stackrel{p(\mathbf{x}|\mathbf{z})\approx p_{\theta }(\mathbf{x}|\mathbf{z})}{\to }\mathbf{x}$$

ELBO in VAE Setting

In variational inference, minimizing the difference (here to minimize the KL divergence) between two probability distributions is equivalent to maximizing the ELBO. Here, we need to minimize ${\mathbb{D}}_{\mathrm{KL}}(q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\Vert p(\mathbf{z}|\mathbf{x}))$, that is, to maximize

$$\mathrm{ELBO}(\mathbf{\varphi })={\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x},\mathbf{z})\right]-{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\log q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$$

However, the ELBO above may not too useful because it involves $p(\mathbf{x},\mathbf{z})$, something we have no access to. So we need to do something more:

$$\boxed{\begin{array}{rl}\mathrm{ELBO}(\mathbf{\varphi })& ={\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x},\mathbf{z})\right]-{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\log q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\\ & ={\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x}|\mathbf{z})\right]+{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{z})\right]-{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\log q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\\ & ={\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log p(\mathbf{x}|\mathbf{z})\right]+{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log \frac{p(\mathbf{z})}{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\right]\\ & =\underset{\text{how good your decoder is}}{\underbrace{{\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}\left[\log p_{\theta }(\mathbf{x}|\mathbf{z})\right]}}+\underset{\text{how good your encoder is}}{\underbrace{\left[-{\mathbb{D}}_{\mathrm{KL}}(q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\Vert p(\mathbf{z}))\right]}}\end{array}}$$

where in the last line we replace $p(\mathbf{x}|\mathbf{z})$ by its proxy $p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})$, and there are two terms:

• Reconstruction. The first term is about the decoder. We want the decoder to produce a good image $\mathbf{x}$ if we feed a latent $\mathbf{z}$ into the decoder. So, we want to maximize $\log p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})$. (We sample $X,Z$ from real distribution $p(\mathbf{x},\mathbf{z})$, and the goal of decoder is to approximate $p_{\mathbf{\theta }}$ to $p$). The expectation here is taken with respect to the samples $\mathbf{z}$ conditioned on $\mathbf{x}$
• Prior Matching. The second term is the KL divergence for the encoder. We want the encoder to turn $\mathbf{x}$ into a latent vector $\mathbf{z}$ such that the latent vector will follow our choice of (good) distribution such as a Gaussian distribution. To conclude, the training goal will be
• Decoder. For given $(\mathbf{z},\mathbf{x})$, find $\mathbf{\theta }$ to maximize $p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})$
• Encoder. For given $(\mathbf{z},\mathbf{x})$, find $\mathbf{\varphi }$ to minimize ${\mathbb{D}}_{\mathrm{KL}}(q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})\Vert p(\mathbf{z}))$

Training VAE

Encoder

We know that $\mathbf{z}$ is generated from the distribution $q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$. We also know that $q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$ should be simple as a Gaussian. Assume that for any give input $\mathbf{x}$ this Gaussian has a mean $\mathbf{\mu }$ and a covariance matrix ${\sigma }^2\text{I}$. We use a deep neural network (DNN) to predict them:

$$\mathbf{\mu }=\underset{\text{DNN}}{\underbrace{{\mathbf{\mu }}_{\mathbf{\varphi }}}}(\mathbf{x}),{\sigma }^2=\underset{\text{DNN}}{\underbrace{{\sigma }_{\mathbf{\varphi }}^2}}(\mathbf{x}),$$

Therefore, the samples ${\mathbf{z}}^{(\ell )}$ can be sampled from the Gaussian distribution

$${\mathbf{z}}^{(\ell )}\sim \mathcal{N}({\mathbf{z}}^{\ell }\mid {\mathbf{\mu }}_{\mathbf{\varphi }}({\mathbf{x}}^{(\ell )}),{\sigma }_{\mathbf{\varphi }}^2({\mathbf{x}}^{(\ell )})\text{I})$$

Decoder

The decoder is implemented through a neural network, denoted as ${\mathrm{decoder}}_{\mathbf{\theta }}$. The job of the decoder network is to take a latent variable $\mathbf{z}$ and generates an image $\hat{\mathbf{x}}$:

$$\hat{\mathbf{x}}={\mathrm{decoder}}_{\mathbf{\theta }}(\mathbf{z})$$

Let's make one more assumption that the decoded image $\hat{\mathbf{x}}$ and the ground truth image $\mathbf{x}$ is Gaussian, that is

$$(\hat{\mathbf{x}}-\mathbf{x})\sim \mathcal{N}(0,{\sigma }_{\mathrm{dec}}^2)$$

Then, it follows that the distribution $p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})$ (marked to be Gaussian)

$$\begin{array}{rl}\log p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})& =\log \mathcal{N}(\mathbf{x}\mid {\mathrm{decode}}_{\mathbf{\theta }}(\mathbf{z}),{\sigma }_{\mathrm{dec}}^2\text{I})\\ & =\log \left\{\frac{1}{\sqrt{(2\pi {\sigma }_{\mathrm{dec}}^2{)}^D}}\exp \left[-\frac{\Vert \mathbf{x}-{\mathrm{decode}}_{\mathbf{\theta }}(\mathbf{z}){\Vert }^2}{2{\sigma }_{\mathrm{dec}}^2}\right]\right\}\\ & =-\frac{\Vert \mathbf{x}-{\mathrm{decode}}_{\mathbf{\theta }}(\mathbf{z}){\Vert }^2}{2{\sigma }_{\mathrm{dec}}^2}-\log \sqrt{(2\pi {\sigma }_{\mathrm{dec}}^2{)}^D}\end{array}$$

where $D$ is the dimension of $\mathbf{x}$. This equation says that the maximization of the likelihood term in ELBO is literally just the ${\ell }_2$ loss between the decoded image and ground truth.

Loss Function

To approximate the expectation, we use Monte-Carlo simulation:

$${\mathbb{E}}_{q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})}[\log p_{\mathbf{\theta }}(\mathbf{x}|\mathbf{z})]\approx \frac{1}{L}\sum _{\ell =1}^L\log p_{\mathbf{\theta }}({\mathbf{x}}^{\ell }|{\mathbf{z}}^{(\ell )}),{\mathbf{z}}^{(\ell )}\sim q_{\mathbf{\varphi }}(\mathbf{z}|{\mathbf{x}}^{(\ell )})$$

where ${\mathbf{x}}^{(\ell )}$ is the $\ell$-th sample in the training set, and the distribution $q_{\mathbf{\theta }}$ is $q_{\mathbf{\varphi }}(\mathbf{z}|{\mathbf{x}}^{(\ell )})=\mathcal{N}(\mathbf{z}\mid {\mathbf{\mu }}_{\mathbf{\varphi }}({\mathbf{x}}^{(\ell )}),{\sigma }_{\mathbf{\varphi }}^2({\mathbf{x}}^{(\ell )})\text{I})$

Now we have the training loss of VAE

$$\underset{\mathbf{\varphi },\mathbf{\theta }}{\mathrm{argmax}}\left\{\frac{1}{L}\sum _{\ell =1}^L\log p_{\mathbf{\theta }}({\mathbf{x}}^{(\ell )}|{\mathbf{z}}^{(\ell )})-{\mathbb{D}}_{\mathrm{KL}}(q_{\mathbf{\varphi }}(\mathbf{z}|{\mathbf{x}}^{(\ell )})\Vert p(\mathbf{z}))\right\}$$

where the first term can be simplified to the ${\ell }_2$ loss between $\mathbf{x}$ and ${\mathrm{decode}}_{\mathbf{\theta }}(\mathbf{z})$ as mentioned above, and the second term can be simplified by the solution of KL divergence between two Gaussian distributions:

$${\mathbb{D}}_{\mathrm{KL}}(\mathcal{N}({\mathbf{\mu }}_0,{\mathbf{\Sigma }}_0),\mathcal{N}({\mathbf{\mu }}_1,{\mathbf{\Sigma }}_1))=\frac{1}{2}\left(\mathrm{Tr}({\mathbf{\Sigma }}_1^{-1}{\mathbf{\Sigma }}_0)-d+({\mathbf{\mu }}_1-{\mathbf{\mu }}_0{)}^T{\mathbf{\Sigma }}_1^{-1}({\mathbf{\mu }}_1-{\mathbf{\mu }}_0)+\log \frac{\det {\mathbf{\Sigma }}_1}{\det {\mathbf{\Sigma }}_0}\right)$$

and in this case ${\mathbf{\mu }}_0={\mathbf{\mu }}_{\mathbf{\varphi }}({\mathbf{x}}^{(\ell )}),{\mathbf{\Sigma }}_0={\sigma }_{\mathbf{\varphi }}^2({\mathbf{x}}^{(\ell )})\text{I},{\mathbf{\mu }}_1=0,{\mathbf{\Sigma }}_1=1$, thus

$${\mathbb{D}}_{\mathrm{KL}}(q_{\mathbf{\varphi }}(\mathbf{z}|{\mathbf{x}}^{(\ell )})\parallel p(\mathbf{z}))=\frac{1}{2}\left(({\sigma }_{\mathbf{\varphi }}^2({\mathbf{x}}^{(\ell )}){)}^d+{\mathbf{\mu }}_{\mathbf{\varphi }}({\mathbf{x}}^{(\ell )}{)}^T{\mathbf{\mu }}_{\mathbf{\varphi }}({\mathbf{x}}^{(\ell )})-d\log ({\sigma }_{\mathbf{\varphi }}^2({\mathbf{x}}^{(\ell )}))\right)$$

where $d$ is the dimension of the vector $\mathbf{z}$

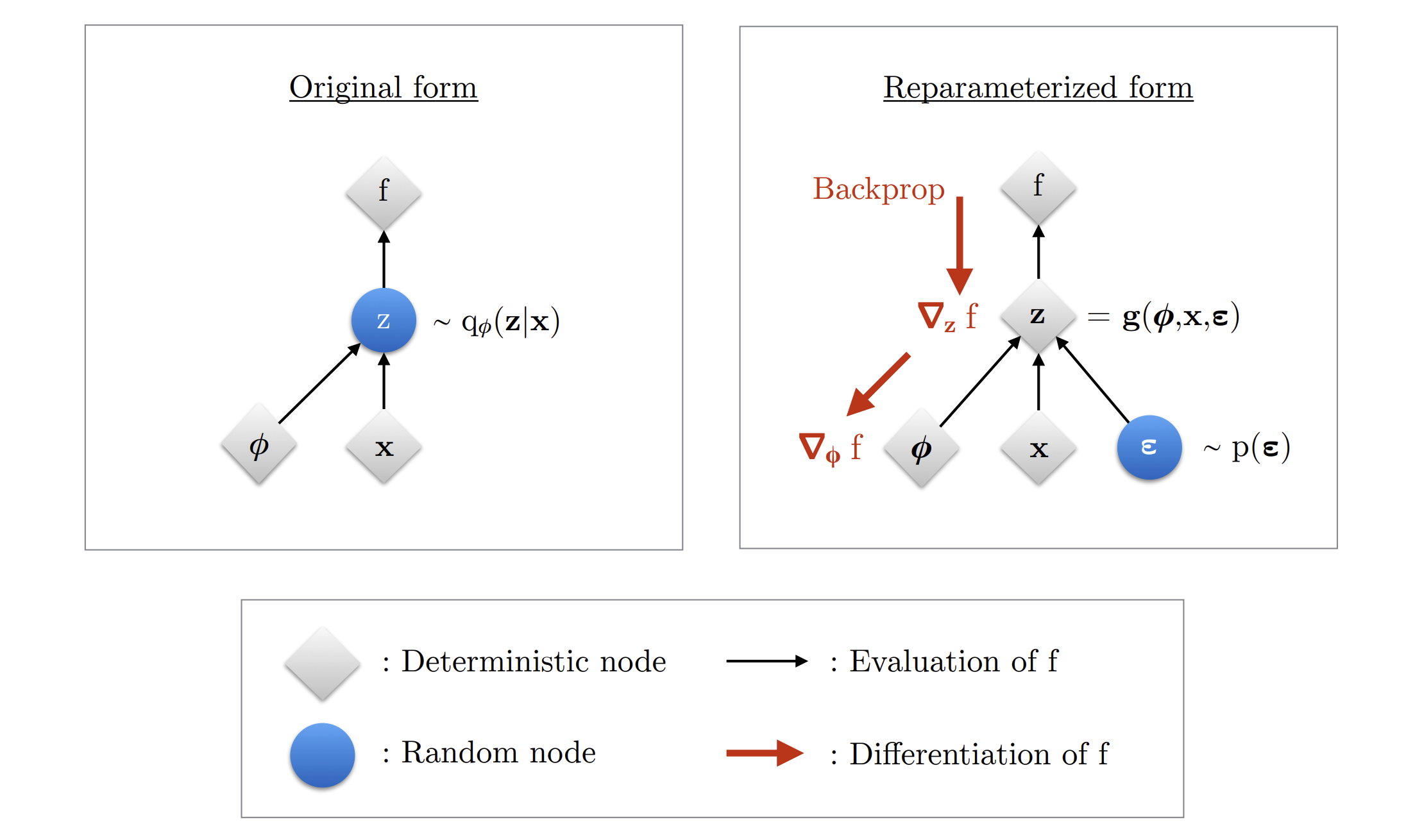
Reparameterization

Note that the latent variable $\mathbf{z}$ in the loss function is sampled from $q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$, which cannot be differentiated during the back-propagation process. So we need to express $\mathbf{z}$ as some differentiable transformation of another random variable $\mathbf{ϵ}$, given $\mathbf{z}$ and $\mathbf{\varphi }$

$$\mathbf{z}=\mathbf{g}(\mathbf{ϵ},\mathbf{\varphi },\mathbf{x})$$

where the distribution of random variable $\mathbf{ϵ}$ is independent of $\mathbf{x}$ and $\mathbf{\varphi }$.

Specifically, the distribution $q_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})$ can be written as:

$$\begin{array}{rl}{q}_{\mathbf{\varphi }}(\mathbf{z}|\mathbf{x})& =\mathcal{N}(\mathbf{z}\mid {\mathbf{\mu }}_{\mathbf{\varphi }}(\mathbf{x}),{\sigma }_{\mathbf{\varphi }}^2(\mathbf{x})\text{I})\\ & ={\mathbf{\mu }}_{\mathbf{\varphi }}(\mathbf{x})+{\sigma }_{\mathbf{\varphi }}(\mathbf{x})\mathcal{N}(0,\text{I})\\ & ={\mathbf{\mu }}_{\mathbf{\varphi }}(\mathbf{x})+{\sigma }_{\mathbf{\varphi }}(\mathbf{x})\mathbf{ϵ}\end{array}$$

where $\mathbf{ϵ}\sim \mathcal{N}(0,\text{I})$. By this way, the gradient of the loss function can be back-propagated to the parameter $\mathbf{\varphi }$

Visualization of Latent Space

The main benefit of a variational autoencoder is that we're capable of learning smooth latent state representations of the input data.

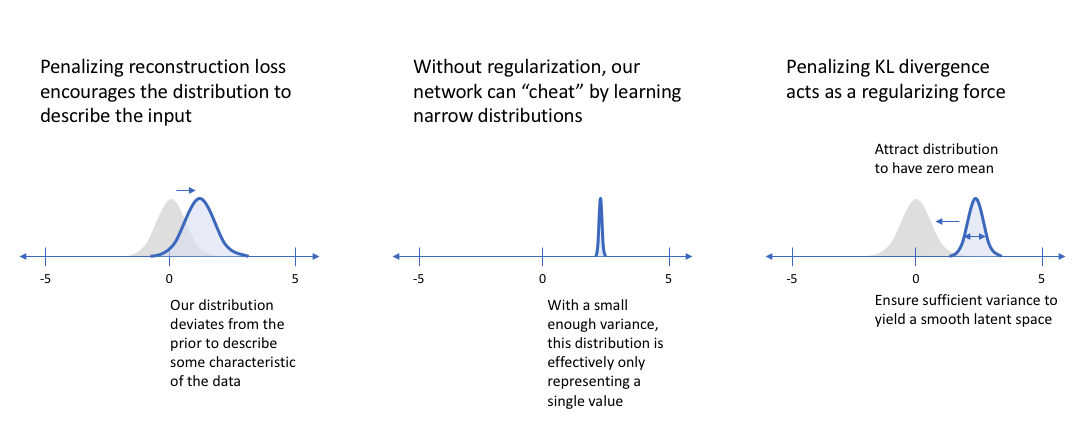
For standard autoencoders, we simply need to learn an encoding which allows us to reproduce the input. As you can see in the left-most figure, focusing only on reconstruction loss does allow us to separate out the classes (in this case, MNIST digits).

However, there's an uneven distribution of data within the latent space. In other words, there are areas in latent space which don't represent any of our observed data. So we cannot just simply sample from the latent space to generate realistic images. 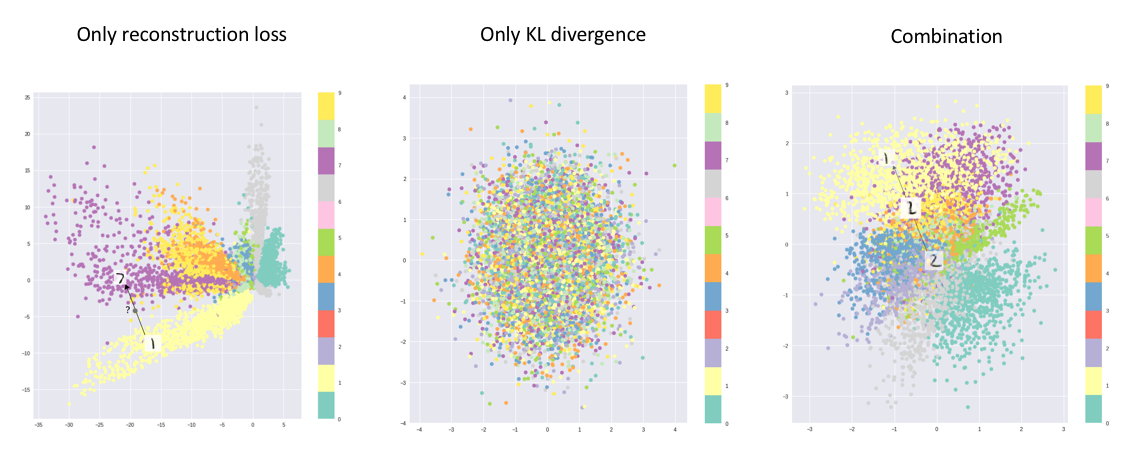On the flip side, if we only focus only on ensuring that the latent distribution is similar to the prior distribution (through our KL divergence loss term), we end up describing every observation using the same unit Gaussian. So we failed to describe the original data from the latent space.