Generative Learning Algorithms

Motivation

Consider a classification problem in which we want to learn to distinguish between elephants ($y=1$) and dogs $(y=0)$, based on some features of an animal. Given a training set, an algorithm like logistic regression or the perceptron algorithm (basically) tries to find a straight line—that is, a decision boundary—that separates the elephants and dogs. Then, to classify a new animal as either an elephant or a dog, it checks on which side of the decision boundary it falls, and makes its prediction accordingly.

Here’s a different approach. First, looking at elephants, we can build a model of what elephants look like. Then, looking at dogs, we can build a separate model of what dogs look like. Finally, to classify a new animal, we can match the new animal against the elephant model, and match it against the dog model, to see whether the new animal looks more like the elephants or more like the dogs we had seen in the training set.

Algorithms that try to learn $p(y|x)$ directly (such as logistic regression), or algorithms that try to learn mapping directly from the space of inputs $\mathcal{X}$ to the labels $\left\{0,1\right\}$ (such as the perceptron algorithm) are called discriminative learning algorithms. Here, we’ll talk about algorithms that instead try to model $p(x|y)$. These algorithms are called generative learning algorithms. For instance, if $y$ indicates whether an example is a dog (0) or an elephant (1), then $p(x|y=0)$ models the distribution of dogs' features, and $p(x|y=1)$ models the distribution of elephant's features.

After modeling $p(y)$ (the class priors) and $p(x|y)$, our algorithm can then use Bayes' Theorem to derive the posterior distribution on $y$ given $x$:

$$p(y|x)=\frac{p(x|y)p(y)}{p(x)}$$

Here the denominator is given by $p(x)=p(x|y=1)p(y=1)+p(x|y=0)p(y=0)$. Actually, if were calculating $p(y|x)$ in order to make a prediction, then we don’t actually need to calculate the denominator, since

$$\begin{array}{rl}\arg \underset{y}{\max }p(y|x)& =\arg \underset{y}{\max }\frac{p(x|y)p(y)}{p(x)}\\ & =\arg \underset{y}{\max }p(x|y)p(y)\end{array}$$

Gaussian Discriminant Analysis (GDA)

Multivariate normal distribution

The multivariate Gaussian distribution is parameterized by a mean vector $\mu \in {\mathbb{R}}^d$ and a covariance matrix $\Sigma \in {\mathbb{R}}^{d\times d}$, where $\Sigma \ge 0$ is symmetric and positive semi-definite. Also written $\mathcal{N}(\mu ,\Sigma )$, its density is given by:

$$p(x;\mu ,\Sigma )=\frac{1}{(2\pi {)}^{d/2}{\left|\Sigma \right|}^{1/2}}\exp \left[-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu )\right]$$

The GDA model

When we have a classification problem in which the input features $x$ are continuous-valued random variables, we can then use the Gaussian Discriminant Analysis (GDA) model, which models $p(x|y)$ using a multivariate normal distribution. The model is:

$$\begin{array}{rl}y& \sim \text{Bernoulli}(\varphi )\\ x\mid y=0& \sim \mathcal{N}({\mu }_0,\Sigma )\\ x\mid y=1& \sim \mathcal{N}({\mu }_1,\Sigma )\end{array}$$

where "Bernoulli" denotes the Bernoulli Distribution. Here, the parameters of our model are $\varphi ,\Sigma ,{\mu }_0$ and ${\mu }_1$. (Note that while there’re two different mean vectors ${\mu }_0$ and ${\mu }_1$, this model is usually applied using only one covariance matrix $\Sigma$.) The log-likelihood of the data is given by

$$\begin{array}{rl}\ell (\varphi ,{\mu }_0,{\mu }_1,\Sigma )& =\log \prod _{i=1}^{n}p\left(x^{(i)},y^{(i)};\varphi ,{\mu }_0,{\mu }_1,\Sigma \right)\\ & =\log \prod _{i=1}^{n}p\left(x^{(i)}|y^{(i)};\varphi ,{\mu }_0,{\mu }_1,\Sigma \right)p\left(y^{(i)};\varphi \right)\end{array}$$

By maximizing $\ell$ with respect to the parameters, we find the maximum likelihood estimate of the parameters to be:

$$\begin{array}{rl}\varphi & =\frac{1}{n}\sum _{i=1}^{n}1\{y^{(i)}=1\}\\ {\mu }_0& =\frac{{\sum }_{i=1}^{n}1\{y^{(i)}=0\}{x}^{(i)}}{{\sum }_{i=1}^{n}1\{y^{(i)}=0\}}\\ {\mu }_1& =\frac{{\sum }_{i=1}^{n}1\{y^{(i)}=1\}{x}^{(i)}}{{\sum }_{i=1}^{n}1\{y^{(i)}=1\}}\\ \Sigma & =\frac{1}{n}\sum _{i=1}^n(x^{(i)}-{\mu }_{y^{(i)}})(x^{(i)}-{\mu }_{y^{(i)}}{)}^T.\end{array}$$

Pictorially, what the algorithm is doing can be seen in as follows: 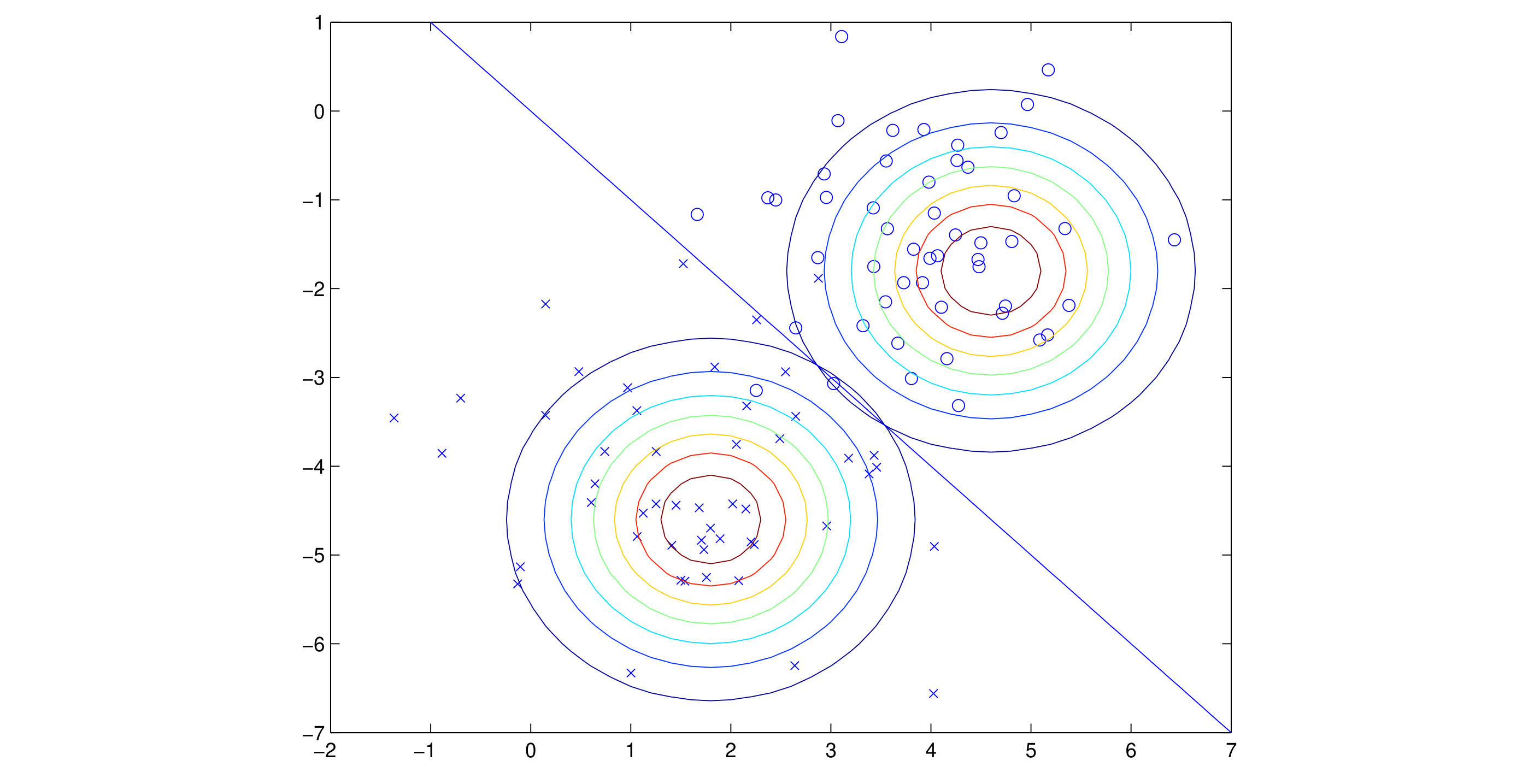Shown in the figure are the training set, as well as the contours of the two Gaussian distributions that have been fit to the data in each of the two classes. Note that the two Gaussians have contours that are the same shape and orientation, since they share a covariance matrix $\Sigma$, but they have different means ${\mu }_0$ and ${\mu }_1$.

Discussion

• Form of $p(y=1|x)$: If $p(x|y)$ is a multivariate Gaussian (with shared $\Sigma$), then $p(y|x)$ necessarily follows a logistic function. Specifically, $p(y=1|x;\varphi ,\Sigma ,{\mu }_0,{\mu }_1)=\frac{1}{1+exp(-{\theta }^{T}x)}$, which is the form logistic regression uses.
• Modeling Assumptions: GDA makes stronger assumptions about the data (specifically, that $p(x|y)$ is Gaussian) than logistic regression. Logistic regression only assumes that $p(y|x)$ takes the form of a logistic function, which can arise from various distributions of $x|y$ (e.g., Gaussian, Poisson).
• Data Efficiency and Accuracy: When GDA's modeling assumptions are correct (or approximately correct), GDA is more data-efficient (requires less training data) and can find better fits, especially with small training datasets. In the limit of very large training sets, GDA is asymptotically efficient.
• Non-Gaussian Data: If the data is non-Gaussian, logistic regression will often perform better than GDA in the limit of large datasets. If we were to use GDA on such data—and fit Gaussian distributions to such non-Gaussian data—then the results will be less predictable, and GDA may (or may not) do well.