Bipartite Graphs

Definition

A simple graph $G$ is called bipartite if its vertex set $V$ can be partitioned into two disjoint sets $V_1$ and $V_2$ such that every edge in the graph connects a vertex in $V_1$ and a vertex in $V_2$ (so that no edge in $G$ connects either two vertices in $V_1$ or two vertices in $V_2$). When this condition holds. we call the pair $(V_1,V_2)$ a bipartition of the vertex set $V$ of $G$.

A simple graph is bipartite if and only if it is possible to assign one of two different color to each vertex of the graph so that no two adjacent vertices are assigned the same color.

Matching

A matching $M$ in a simple graph $G=(V,E)$ is a subset of the set $E$ of edges of the graph such that no two edges are incident with the same vertex. In other words, a matching is a subset of edges such that if $\left\{s,t\right\}$ and $\left\{u,v\right\}$ are distinct edges of the matching, the $s,t,u$ and $v$ are distinct.

A vertex that is the endpoint of a matching $M$ is said to be matched in $M$; otherwise it is said to be unmatched. A maximum matching is a matching with the largest number of edges.

We say that a matching $M$ in a bipartite graph $G=(V,E)$ with bipartition $(V_1,V_2)$ is a complete matching from $V_1$ to $V_2$ if every vertex in $V_1$ is the endpoint of an edge in the matching, or equivalently, if $\left|M\right|=\left|V_1\right|$.

Hall's Marriage Theorem

The bipartite graph $G=(V,E)$ with bipartition $(V_1,V_2)$ has a complete matching from $V_1$ to $V_2$ if and only if $\left|N(A)\right|\ge \left|A\right|$ for all subsets $A$ of $V_1$, where $N(A)$ denotes the neighborhood of $A$.

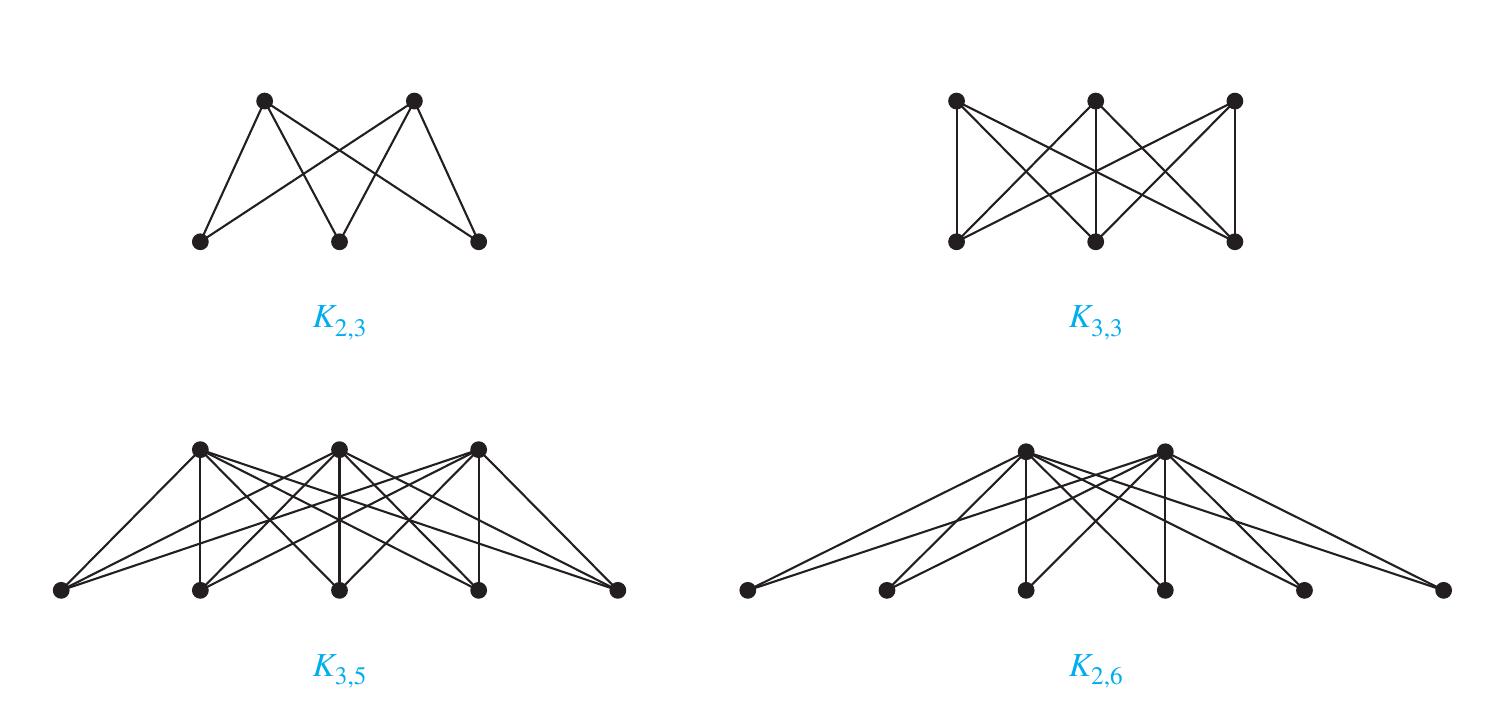
Complete Bipartite Graphs

A complete bipartite graph $K_{m,n}$ is a graph that has its vertex set partitioned into two subsets of $m$ and $n$ vertices, respectively with an edge between two vertices if and only if one vertex is in the first subset ant the other vertex is the second subset.