Planar Graphs

Definition

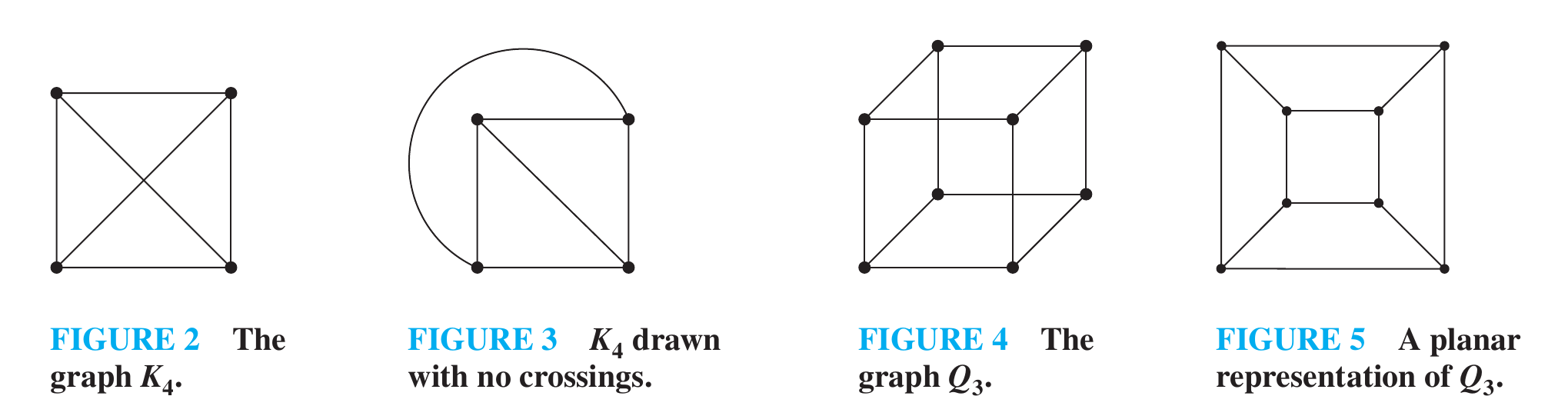
In graph theory, a planar graph is a graph that can be drawn on a plane without any edges crossing. More formally, a graph is planar if it can be embedded in the plane (or equivalently, a sphere), meaning each vertex is mapped to a distinct point on the plane and each edge is mapped to a continuous curve (without self-intersections) such that no two curves representing edges intersect except possibly at their endpoints (the vertices).

Euler's Formula

When a planar graph is drawn, it divides the plane into distinct regions (faces). There's always one unlimited outer face.

Euler's Formula is a fundamental theorem in graph theory that relates the number of vertices, edges, and regions in a connected planar graph. It states that for any connected planar graph, the following equation holds:

$$v-e+r=2$$

• $v$ is the number of vertices (nodes) in the graph.
• $e$ is the number of edges in the graph.
• $r$ is the number of regions (faces) in the graph's planar drawing, including the infinite outer region

Warning

We cannot use Euler's Formula to prove whether a graph is planar or not, since if we don't draw the graph in a plane, we have no idea what the faces are!

However, Euler’s formula can be used to establish some inequalities that must be satisfied by planar graphs.

Corollary 1

If $G$ is a connected planar simple graph with $e$ edges and $v$ vertices, where $v\ge 3$, then $e\le 3v-6$

This corollary tells us that in a simple planar graph, the number of edges is limited by the number of vertices. It's about how "dense" a graph can be while still being planar.

In a simple planar graph, each face is bounded by at least $3$ edges (a triangle being the smallest possible face). Also, each edge is on the boundary of at exactly $2$ faces. Let's sum all the edges per face, we have

$$2e=\sum _{\text{all regions}R}\text{num of bounded edges of}R\ge 3r$$

Hence with Euler's formula

$$2e\ge 3r⟹e\le 3v-6$$

Corollary 2

If $G$ is a connected planar simple graph, then $G$ has a vertex of degree not exceeding five.

Planarity forces some vertices to have relatively few connections. You can't have all vertices highly connected while maintaining planarity. At least one vertex must have at most $5$ connections. This implies that planar graphs are sparse, as in there usually aren't a large amount of connections.

Corollary 3

If a connected planar simple graph has $e$ edges and $v$ vertices with $v\ge 3$ and no circuits of length three, then $e\le 2v-4$

.

Kuratowski's Theorem

Kuratowski's Theorem provides a necessary and sufficient condition for a graph to be planar. The theorem states that a graph is planar if and only if it does not contain a subgraph that is a subdivision of either $K_5$ (the complete graph on $5$ vertices) or $K_{3,3}$ (the complete bipartite graph on two sets of $3$ vertices each).

Subdivision of a Graph (Homeomorphic Graph)

A graph obtained from another graph by replacing some of its edges with a path consisting of one or more vertices. In other words, you can 'insert' new vertices along the edges of a graph to create a subdivision (or homeomorphic graph)

Figure: Homeomorphic Graphs

Therefore, Kuratowski's Theorem provides a powerful way to test if a given graph is planar by looking for specific subgraphs. If one of them is not present, then the graph is planar. If one of them is present, then the graph is not planar.