Euler Integral

Gamma函数

定义$\Gamma$函数

$$\Gamma (s)={\int }_0^{+\infty }{x}^{s-1}{e}^{-x}\mathrm{d}x$$

这个函数可以被写成两个积分之和

$$\Gamma (s)={\int }_0^1{x}^{s-1}{e}^{-x}\mathrm{d}x+{\int }_1^{+\infty }{x}^{s-1}{e}^{-x}\mathrm{d}x=\Phi (s)+\Psi (s)$$

其中$\Phi (s)$在$s\ge 1$时是正常积分, 在$0<s<1$时是收敛的无界函数的反常积分（由Cauchy判据） $\Psi (s)$当$s>0$时也是收敛的无穷限反常积分（由Cauchy判据） 所以$\Gamma (s)$在${\mathbb{R}}^{+}$上收敛, 规定其定义域为$s>0$

Gamma函数的性质

1. $\Gamma (s)$在$(0,+\infty )$上连续可导

$$\begin{array}{rl}{\Gamma }^{\prime }(s)& ={\int }_0^{+\infty }{x}^{s-1}{e}^{-x}\ln x\mathrm{d}x\\ {\Gamma }^{(n)}(s)& ={\int }_0^{+\infty }{x}^{s-1}(\ln x{)}^n\mathrm{d}x\end{array}$$

2. 满足递推公式

$$\Gamma (s+1)=s\Gamma (s)$$

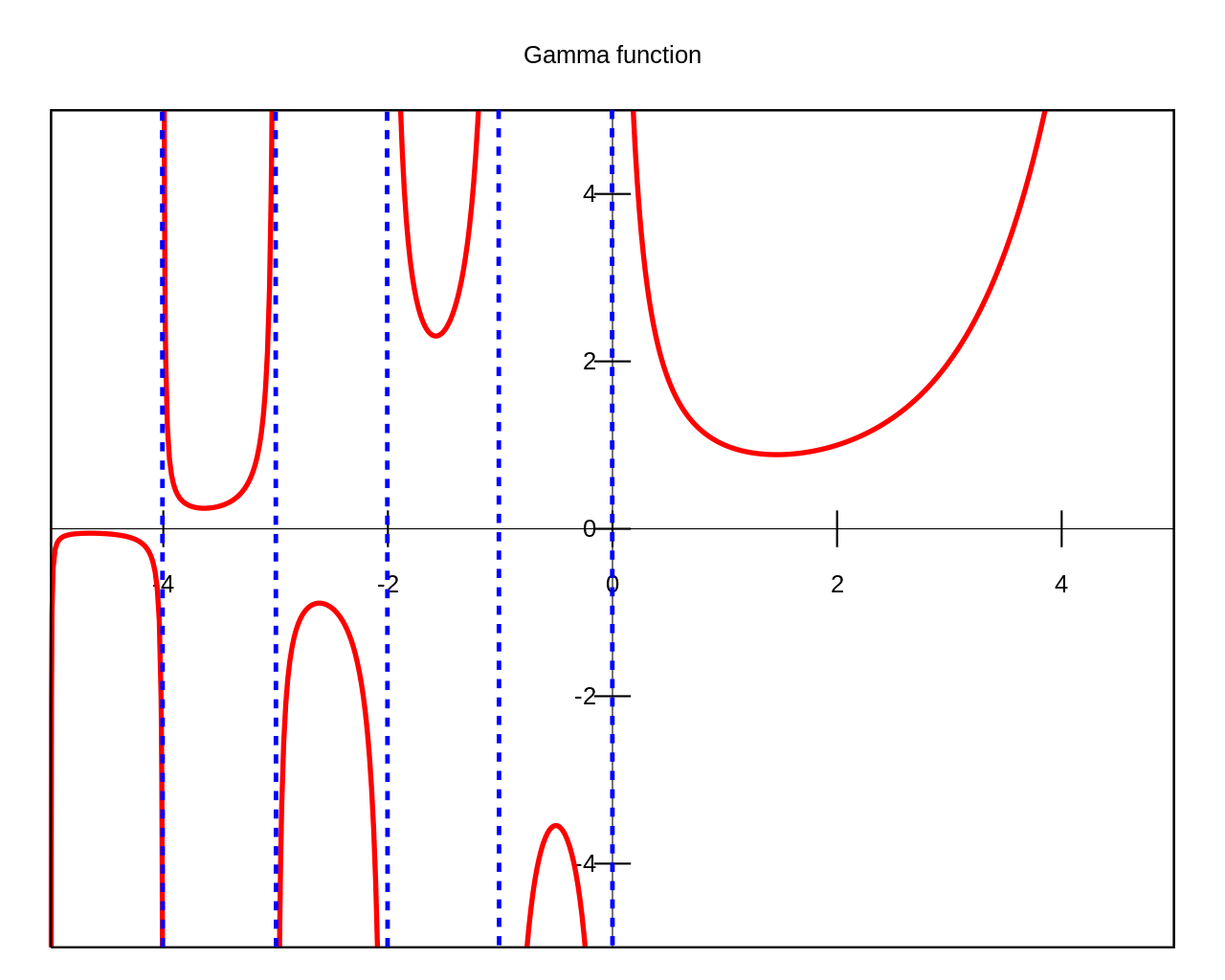
特别地, 当$s=n\in {\mathbb{N}}^{\ast }$时, 有$\Gamma (n+1)=n!$ 3. 图像（利用递推公式延拓定义域后）

Beta函数

定义$B$函数

$$B(p,q)={\int }_0^1{x}^{p-1}(1-x{)}^{q-1}\mathrm{d}x$$

同样由函数的收敛性, 规定定义域为$p,q>0$

Beta函数的性质

1. $B(p,q)$在${\mathbb{R}}^{+}\times {\mathbb{R}}^{+}$上连续
2. 对称性$B(p,q)=B(q,p)$
3. 递推公式

$$\begin{array}{rl}B(p,q)& =\frac{q-1}{p+q-1}B(p,q-1)\\ B(p,q)& =\frac{p-1}{p+q-1}B(p-1,q)\\ ⟹B(p,q)& =\frac{(p-1)(q-1)}{(p+q-1)(p+q-2)}\end{array}$$

4. 常见的其他形式 令$x={\cos }^2\varphi$, 就有

$$B(p,q)=2{\int }_0^{\pi /2}{\sin }^{2q-1}\varphi {\cos }^{2p-1}\varphi \mathrm{d}\varphi$$

令$x=\frac{y}{1+y}$, 就有

$$B(p,q)={\int }_0^{+\infty }\frac{y^{p-1}}{(1+y{)}^{p+q}}\mathrm{d}y$$

设$y=\frac{1}{t}$, 我们有

$${\int }_1^{+\infty }\frac{y^{p-1}}{(1+y{)}^{p+q}}\mathrm{d}y+{\int }_1^0\frac{t^{q-1}}{(1+t{)}^{p+q}}=0$$

可以得出更对称的形式

$$B(p,q)={\int }_0^1\frac{y^{p-1}+y^{q-1}}{(1+y{)}^{p+q}}$$

Gamma函数和Beta函数之间的关系

关系公式

$$B(p,q)=\frac{\Gamma (p)\Gamma (q)}{\Gamma (p+q)}$$

应用: 计算$\Gamma (1/2)$

考虑

$$B(a,1-a)=\frac{\Gamma (a)\Gamma (1-a)}{\Gamma (1)}=\Gamma (a)\Gamma (1-a)$$

即

$${\int }_0^{+\infty }\frac{y^{a-1}}{1+y}\mathrm{d}y=\Gamma (a)\Gamma (1-a)$$

取$a=\frac{1}{2}$就有

$$\Gamma (\frac{1}{2})=\sqrt{{\int }_0^{+\infty }\frac{x^{-1/2}}{1+x}\mathrm{d}x}=\sqrt{{\int }_0^{+\infty }\frac{2\mathrm{d}t}{(1+t^2)}}=\sqrt{\pi }$$

又因为

$$\Gamma (s)={\int }_0^{+\infty }{x}^{s-1}{e}^{-x}\mathrm{d}x=2{\int }_0^{+\infty }{t}^{2s-1}{e}^{-t^2}\mathrm{d}t$$

取$s=\frac{1}{2}$就有

$$\boxed{{\int }_0^{+\infty }{e}^{-x^2}\mathrm{d}x=\frac{\sqrt{\pi }}{2}}$$

应用: 计算Wallis积分

回忆Wallis积分

$${\int }_0^{\pi /2}{\sin }^{n}x\mathrm{d}x=\{\begin{array}{ll}\frac{(n-1)!!}{n!!}\cdot \frac{\pi }{2}& ,\text{n为偶数}\\ \frac{(n-1)!!}{n!!}& ,\text{n为奇数}\end{array}$$

考虑

$$\begin{array}{rl}{\int }_0^{\pi /2}{\sin }^{2n+1}x\mathrm{d}x& ={\int }_0^{\pi /2}{\sin }^{2(n+1)-1}\varphi {\cos }^{2(1/2)-1}\varphi \mathrm{d}\varphi \\ & =\frac{1}{2}B(n+1,\frac{1}{2})=\frac{1}{2}\frac{\Gamma (n+1)\Gamma (\frac{1}{2})}{\Gamma (n+\frac{3}{2})}\\ & =\frac{1}{2}\frac{n!\sqrt{\pi }}{(n+\frac{1}{2})\Gamma (n+\frac{1}{2})}\\ & =\frac{1}{2}\frac{n!\sqrt{\pi }}{(n+\frac{1}{2})(n-\frac{1}{2})(n-\frac{3}{2})\cdots (\frac{1}{2})\sqrt{\pi }}\\ & =\frac{1}{2}\frac{n!\cdot 2^{n+1}}{(2n+1)!!}=\frac{(2n)!!}{(2n+1)!!}\end{array}$$

得到奇数的情况, 同理也可以计算出偶数的情况