Fourier Series

In Real Case

See Fourier Series (Real)

Relation with Fourier Transform

See Fourier Series as Special Case of Fourier Transform

Definition

Continuous Fourier Transform (CFS)

$$x(t)=\sum _{k=-\infty }^{\infty }{a}_k\exp \left(jk{\omega }_{0}t\right),\text{where}{a}_k=\frac{1}{T}{\int }_0^{T}x(t)\exp (-jk{\omega }_{0}t)\mathrm{d}t$$

And we can denote this as

$$x(t)\stackrel{FS}{\leftrightarrow }{a}_k$$

Discrete Fourier Transform (DFS)

$$a_k=\frac{1}{N}\sum _{n=0}^{N-1}x(n)\exp \left(-jk{\omega }_{0}n\right)$$

where ${\omega }_0=\frac{2\pi }{T}=\frac{2\pi }{N}$. Similarly,

$$x[n]=\sum _{k=0}^{N-1}{a}_k\exp (jk{\omega }_{0}n)$$

Properties

1. If $x(t)\stackrel{FS}{\leftrightarrow }{a}_k$ and $y(t)\stackrel{FS}{\leftrightarrow }{b}_k$ with the same period $T$, then

$$x(t)\ast y(t)\stackrel{FS}{\leftrightarrow }T{a}_k{b}_k$$

and

$$x(t)y(t)\stackrel{FS}{\leftrightarrow }\sum _{l=-\infty }^{\infty }{a}_l{b}_{k-1}=a_k\ast b_k$$

Note

Why there is a $T$ in the first formula?

Because the signals are periodic with period $T$, when you do this integration, you're accumulating over one full period $T$. This $T$ factor comes from the integration bounds in the convolution integral.

In contrast, when you simply multiply two signals in the time domain (second equation), there's no integration involved - you're just multiplying the values at each point. Therefore, no $T$ factor appears.

2. If $x(t)\stackrel{FS}{\leftrightarrow }{a}_k$, then

$$x(t-t_0)=x(t)\ast \delta (t-t_0)\stackrel{FS}{\leftrightarrow }\exp (-j\omega t_0)a_k=\exp (-jk{\omega }_0{t}_0)a_k$$

3. If $x(t)\stackrel{FS}{\leftrightarrow }{a}_k$, then

$$x(\alpha t)\stackrel{FS}{\leftrightarrow }{a}_k$$

Note that here we would have a new $T_1=\frac{T}{\alpha }$ 4. If $x(t)\stackrel{FS}{\leftrightarrow }{a}_k$, then

$$x^{\prime }(t)=x(t)\ast {\delta }^{\prime }(t)\stackrel{FS}{\leftrightarrow }{a}_k\cdot jk{\omega }_0$$

Examples

Square Waves

CT Case

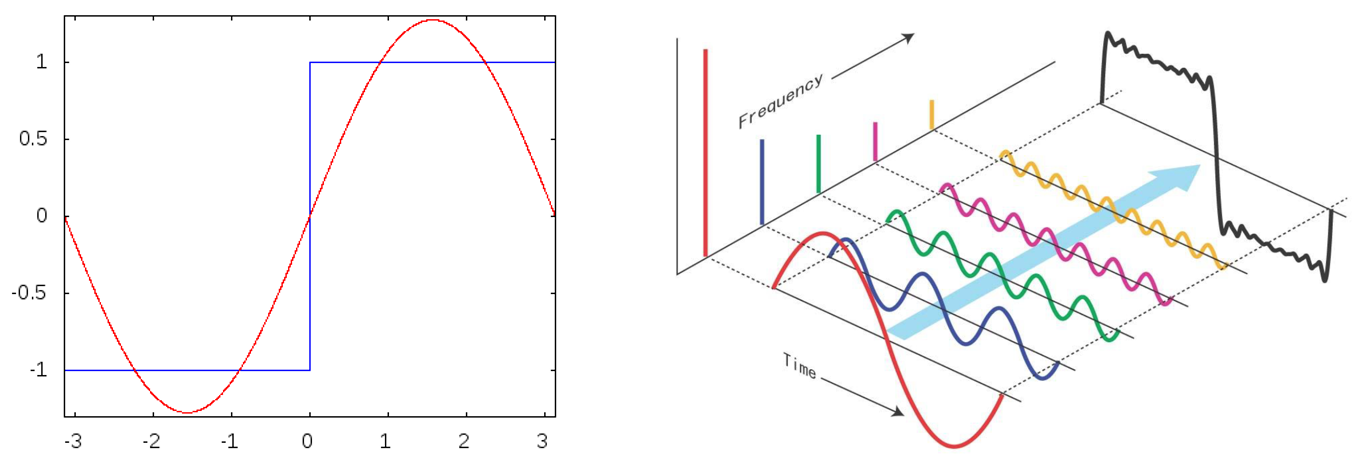Consider a square wave signal with the following representation

$$x(t+NT)=\{\begin{array}{ll}1,& \left|t\right|<T_1\\ 0,& T_1<\left|t\right|<\frac{T}{2}\end{array},N=0,1,2,\dots$$

We assume the Fourier Series is $x(t)=\sum _{k=-\infty }^{\infty }{a}_k\exp \left(jk{\omega }_{0}t\right)$ where ${\omega }_0=\frac{2\pi }{T}$, then we have

$$a_0=\frac{1}{T}{\int }_{-T/2}^{T/2}x(t)\mathrm{d}t=\frac{1}{T}{\int }_{-T_1}^{T_1}1\mathrm{d}t=\frac{2T_1}{T}$$

and

$$\begin{array}{rl}{a}_k& =\frac{1}{T}{\int }_{-T/2}^{T/2}x(t)\exp \left(jk{\omega }_{0}t\right)\mathrm{d}t\\ & =\frac{1}{T}{\int }_{-T_1}^{T_1}\exp (jk{\omega }_{0}t)\mathrm{d}t\\ & =-\frac{1}{jk{\omega }_{0}T}\left[\exp (-jk{\omega }_0{T}_1)-\exp (jk{\omega }_0{T}_1)\right]\\ & =\frac{2\sin (k{\omega }_0{T}_1)}{k{\omega }_{0}T}\\ & =\frac{\sin (k{\omega }_0{T}_1)}{k\pi }\end{array}$$

Using Sinc function, we can rewrite $a_k$ as

$$a_k=\frac{\sin \left(k{\omega }_0{T}_1\right)}{k\pi }=\frac{2T_1}{T}\mathrm{sinc}\left(k{\omega }_0{T}_1\right)=\frac{2T_1}{T}\mathrm{sinc}\left(2k\pi \frac{T_1}{T}\right)$$

If we let $\lambda =\frac{2T_1}{T}$ be valid length of the square signal, we can just have $a_k=\lambda \mathrm{sinc}\left(\lambda k\pi \right)$

DT Case

For

$$x[n]=1,-N_1+rN\le n\le N_1+rN$$

We have

$$a_k=\frac{\sin (\lambda k\pi )}{N\sin \left(\frac{k\pi }{N}\right)}$$

Dirac Comb

For the Dirac Comb $x(t)=\sum _{k=-\infty }^{\infty }\delta (t-kT)$, we have

$$T\sum _{k=-\infty }^{\infty }\delta (t-kT)=\sum _{k=-\infty }^{\infty }\exp (jk{\omega }_{0}t),{\omega }_0=\frac{2\pi }{T}$$

Therefore, $a_k=\frac{1}{T},k=0,\pm 1,\pm 2,\dots$