Partially Ordered Set

Definition

A relation $R$ on a set $S$ is called a partial ordering or partial order if it is reflexive, antisymmetric and transitive. A set $S$ together with a partial ordering $R$ is called a partially ordered set, or poset, and is denoted by $(S,R)$. Members of $S$ are called the elements of the poset.

Example

$(\mathbb{Z},\le )$ and $({\mathbb{N}}^{\ast },\mid )$ are posets

Well-Ordered

The elements $a$ and $b$ of a poset $(S,⪯)$ are called comparable if $a⪯b$ or $b⪯a$. When $a$ and $b$ are elements of $S$ such that neither $a⪯b$ nor $b⪯a$, $a$ and $b$ are called incomparable.

The adjective “partial” is used to describe partial orderings because pairs of elements may be incomparable. When every two elements in the set are comparable, the relation is called a total ordering.

If $(S,⪯)$ is a poset and every two elements of $S$ are comparable, $S$ is called totally ordered or linearly ordered set, and $⪯$ is called a total order or a linear order. A totally ordered set is also called a chain.

Example

$(\mathbb{Z},\le )$ is totally ordered, while $({\mathbb{N}}^{\ast },\mid )$ is not.

$(S,⪯)$ is a well-ordered set is its a poset such that $⪯$ is a total ordering and every non-empty subset of $S$ has a least element.

The Principle of Well-ordered Induction

Suppose that $S$ is a well-ordered set. Then $P(x)$ is true for all $x\in S$,if

• For every $y\in S$, if $P(x)$ is true for all $x\in S$ with $x\prec y$, then $P(y)$ is true.

This is a generation of mathematical induction

Note

We do not need a basis step in a proof using the principle of well-ordered induction because if $x_0$ is the least element of a well-ordered set, the inductive step tells us that $P(x_0)$ is true. This follows because there are no elements $x\in S$ with $x\prec x_0$ , so we know that $P(x)$ is true for all $x\in S$ with $x\prec x_0$ .

Lexicographic Order

The lexicographic ordering $⪯$ on $A_1\times A_2$ is defined by specifying that $(a_1,a_2)\prec (b_1,b_2)$ if and only if either $a_1\prec b_1$ or both $a_1=b_1$ and $a_2\prec b_2$. Then we obtain a partial ordering $⪯$ by adding equality to the ordering $\prec$ on $A_1\times A_2$.

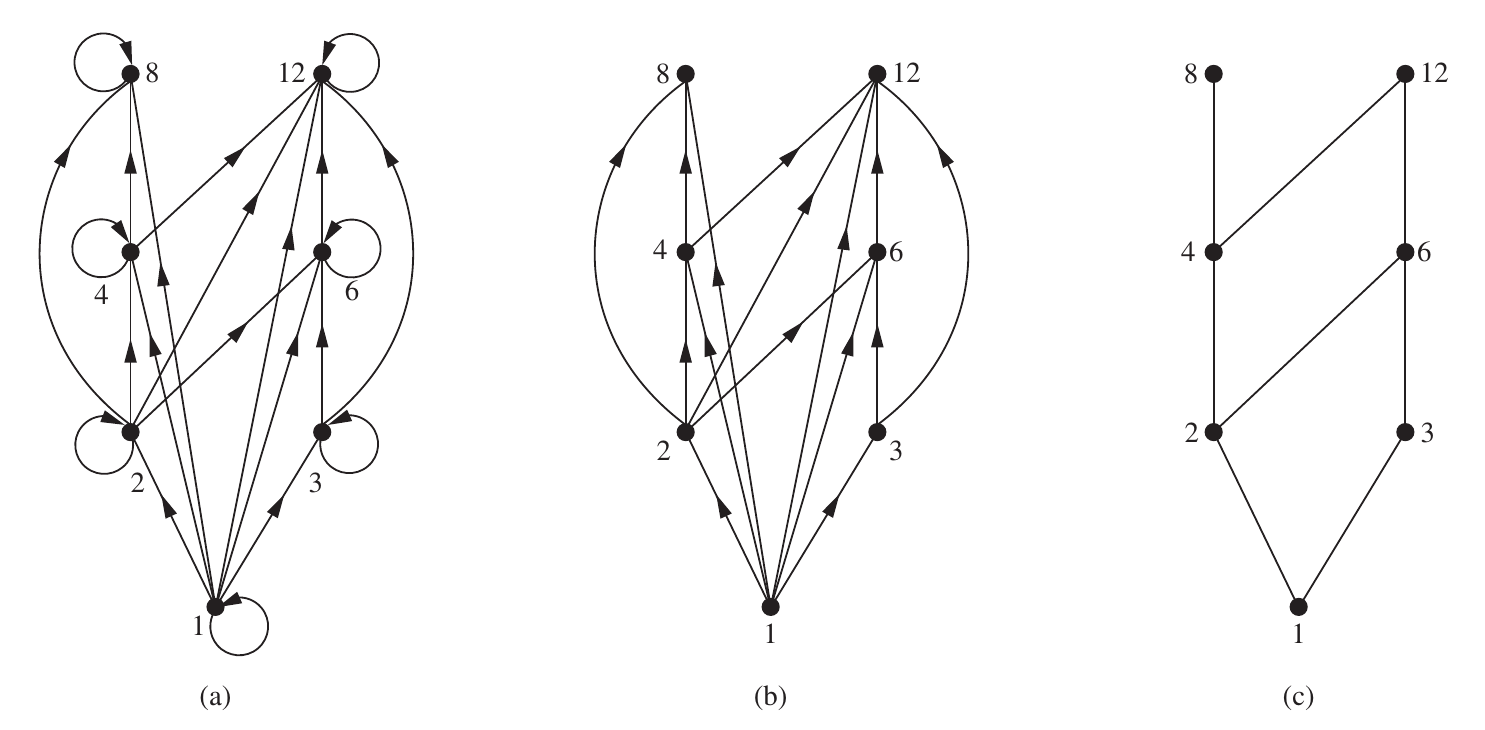
Hasse Diagram

Hasse diagram illustrates the relationships between elements of the poset by depicting them as vertices connected by line segments, which indicate the order relations among them.

• Each element of the poset is represented as a point (or vertex) in the diagram. The points are arranged in such a way that if one element is less than another ($p\prec q$), the point for $p$ appears lower than that for $q$ in the diagram
• A line segment is drawn between two points if one element covers another. An element $a$ covers $b$ if $b\prec a$ and there is no element $c$ such that $b\prec c\prec a$. This means that the diagram does not include redundant connections, simplifying the representation

The following figure shows the process to construct the Hasse diagram of $(\left\{1,2,3,4,5,6,8,12\right\},\mid )$

Maximal and Minimal Elements

$a$ is maximal in the poset $(S,⪯)$ is there is no $b\in S$ such that $a\prec b$. $a$ is minimal in the poset $(S,⪯)$ is there is no $b\in S$ such that $b\prec a$.

Maximal and minimal elements are easy to spot using a Hasse diagram. They are the “top” and “bottom” elements in the diagram.

$a$ is the greatest element of the poset $(S,⪯)$ if $b⪯a$ for all $b\in S$. The greatest element is unique when it exists $a$ is the least element of the poset $(S,⪯)$ if $a⪯b$ for all $b\in S$. The least element is unique when it exists.

Sometimes it is possible to find an element that is greater than or equal to all the elements in a subset $A$ of a poset $(S,⪯)$.

If $u$ is an element of $S$ such that $a⪯u$ for all elements $a\in A$, then $u$ is called an upper bound of $A$. Likewise, if $l$ is an element of $S$ such that $l⪯a$ for all elements $a\in A$, then $l$ is called a lower bound of $A$.

The element $x$ is called the least upper bound of the subset $A$ if $x$ is an upper bound that is less than every other upper bound of $A$. Similarly, the element $y$ is called the greatest lower bound of $A$ if $y$ is greater than every other lower bound of $A$.

Lattices

A partially ordered set in which every pair of elements has both a least upper bound and a greatest lower bound is called a lattice.

For example, the poset $({\mathbb{Z}}^{+},\mid )$ is a lattice: Let $a$ and $b$ be two positive integers. The least upper bound and greatest lower bound of these two integers are the least common multiple and the greatest common divisor of these integers, respectively.

Topological Sorting

The goal of topological sorting is to convert the partial order into a total order, where every pair of elements is comparable. This is particularly useful in scenarios like scheduling tasks where certain tasks must precede others.

1. Identify Minimal Elements: Begin with the poset and identify minimal elements (elements that have no predecessors).
2. Remove and Record: Remove one minimal element from the set and record it in the output list.
3. Repeat: Continue this process until all elements have been removed from the poset.

The output will be a linear sequence of elements such that if $a⪯b$, then aa appears before bb in the list