可逆过程和不可逆过程
一个系统由某一状态出发，经过某一过程后到达另一个状态. 如果存在另一个过程使得系统和外界都完全复原（即系统恢复到原来的状态，同时消除对外界的一切影响），则称原来的过程为可逆过程；反之，如果用任何方式都不能使系统和外界同时完全复原，则称原来的过程为不可逆过程.
无摩擦力和其它损失的准静态过程是可逆过程；有摩擦力或其它损失的准静态过程是不可逆过程；而非静态过程是不可逆过程
Tip
区分可逆过程和不可逆过程的判据不在于反过程能否发生，而**在于反过程能否同时消除原过程对系统和外界造成的影响. **
比如对于自由膨胀过程，其膨胀过程没有内能改变，也没有做功和热量传递；但是要使其压缩还原到原来的状态，就必须要对其做功，且系统放热，故它为不可逆过程
不可逆因素
- 耗散不可逆因素：有摩擦力或其它耗散
- 力学不可逆因素：如系统内部各部分之间的压强差不是无穷小
- 热学不可逆因素：如系统内部各部分之间的温度差不是无穷小
- 化学不可逆因素：如系统内部各部分之间化学成分的差异不是无穷小
可逆过程是一种理想化过程，实际上并不存在
热力学第二定律
热力学第一定律的局限性
- 不能判定自然过程进行的方向；
- 不能给出热力学过程进行的限度
第二类永动机
如果一种热机的工作物质在此循环过程中，从高温热源吸收热量并全部用来做功，而工作物质本身又回到原来的热力学状态，则此热机称为第二类永动机；这样的热机的热机效率为
第二类永动机并不违反热力学第一定律，即不违反能量守恒定律，因而对人们更具诱惑性
在提高热机效率时进行的大量实验事实说明：在任何情况下，热机都不可能只有一个热源. 由此Kelvin在1851年提出了热力学第二定律
热力学第二定律的两种基本表述
Kelvin表述
不可能从单一热源吸收热量，使之全部转化为有用的功而不产生其它影响.
其中
- 单一热源指温度均匀且恒定不变的热源；
- 其它影响指除了由单一热源吸热，把所吸收的热用来做功以外的任何其他变化
这说明效率为的热机是不存在的
Kelvin表述表明了热功转换的不可逆性：功转化为热可以自发地进行；热转化为功却不能在不对外界产生其它影响的条件下自发地进行
Clausius表述
不可能把热量从低温物体转移到高温物体而不产生其它影响
也就是说制冷系数等于无穷大的制冷机是不可能制造成功的
Calusius表述表明了热传递的不可逆性
两种表述的等价性
- 若Clausius表述不正确，则Kelvin表述也不正确：可以把某一热机向低温热源放的热全部释放到高温热源，那么就相当于实现了一个只需要一个热源的热机
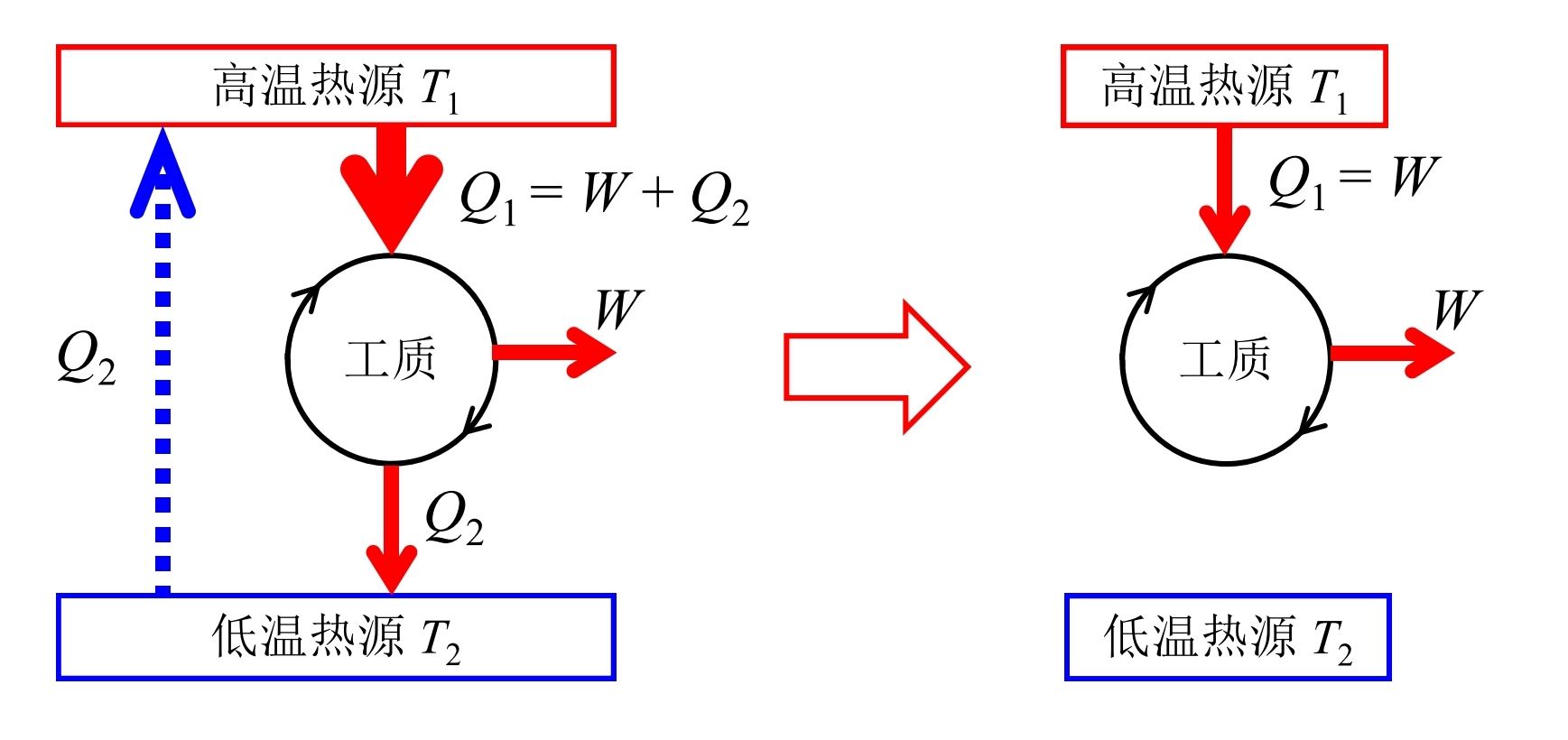
- 若Kelvin表述不正确，则Calusius表述也不正确：如果存在这样一个热机能够从高温热源吸收热量全部转化为功驱动一个制冷机，这一个制冷剂从低温热源吸取热量并向高温热源放出的热量，这整体就相当于从低温热源吸收了热量并全部传递到了高温热源，这违反了Calusius表述
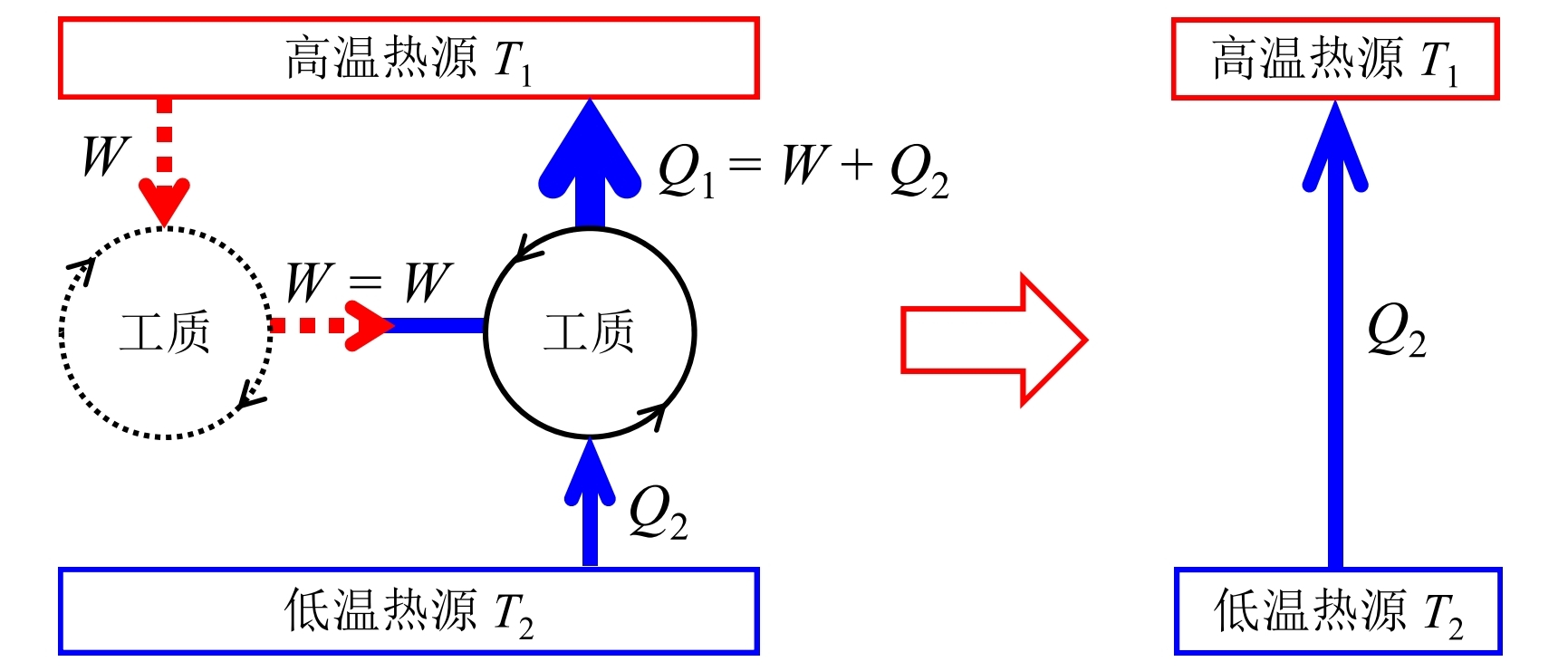
物理实质
自然界一切与热现象有关的实际宏观过程都是不可逆的；热力学第二定律的Kelvin表述和Calusius表述分别是对热功转换和热传递过程不可逆性的具体表述，且这两种不可逆性是相互关联且等价的
绝热膨胀是不可逆的
若不然，则可以设计一个单一热源给予气体热量令其膨胀做功，而该气体可以自动地在绝热条件下收缩到初态，这就形成了一个从单一热源吸热做功的第二类永动机
绝热线不能相交
由热力学第二定律可知，图上的两条绝热线不可能相交，否则再画一条等温线和这两套绝热线分别相交，就构成了只有一个热源的循环过程
气体扩散是不可逆的
若不然，假设均匀混合的气体A,B可以自发地分离，使得容器左边全为气体A，容器右边全为气体B，那么我们可以在两种气体的分界面处设置两个连接外部做功装置的半透膜活塞，靠左边的半透膜活塞只允许A气体的分子通过，靠右边的半透膜活塞只允许B气体的分子通过. 这时如果外部热源为气体A,B的分子提供穿越半透膜膨胀的能量，那么A气体将穿过左边的半透膜活塞推动右边的半透膜活塞对外做功，直到其膨胀至占满整个容器；B气体将穿过右边的半透膜活塞推动左边的半透膜活塞对外做功，直到其膨胀至占满整个容器，最后又回到两种气体均匀混合的初始状态.
而这就形成了一个从单一热源吸热做功的系统
热力学第二定律的统计意义
自由膨胀实验
一个被隔板分为左、右相等两部分的容器. 开始时，所有的N个分子都在左边. 抽出隔板后分子将向右边扩散，平衡后所有分子都将在整个容器内无规则运动.
以为例，分子可能的分布列举如下
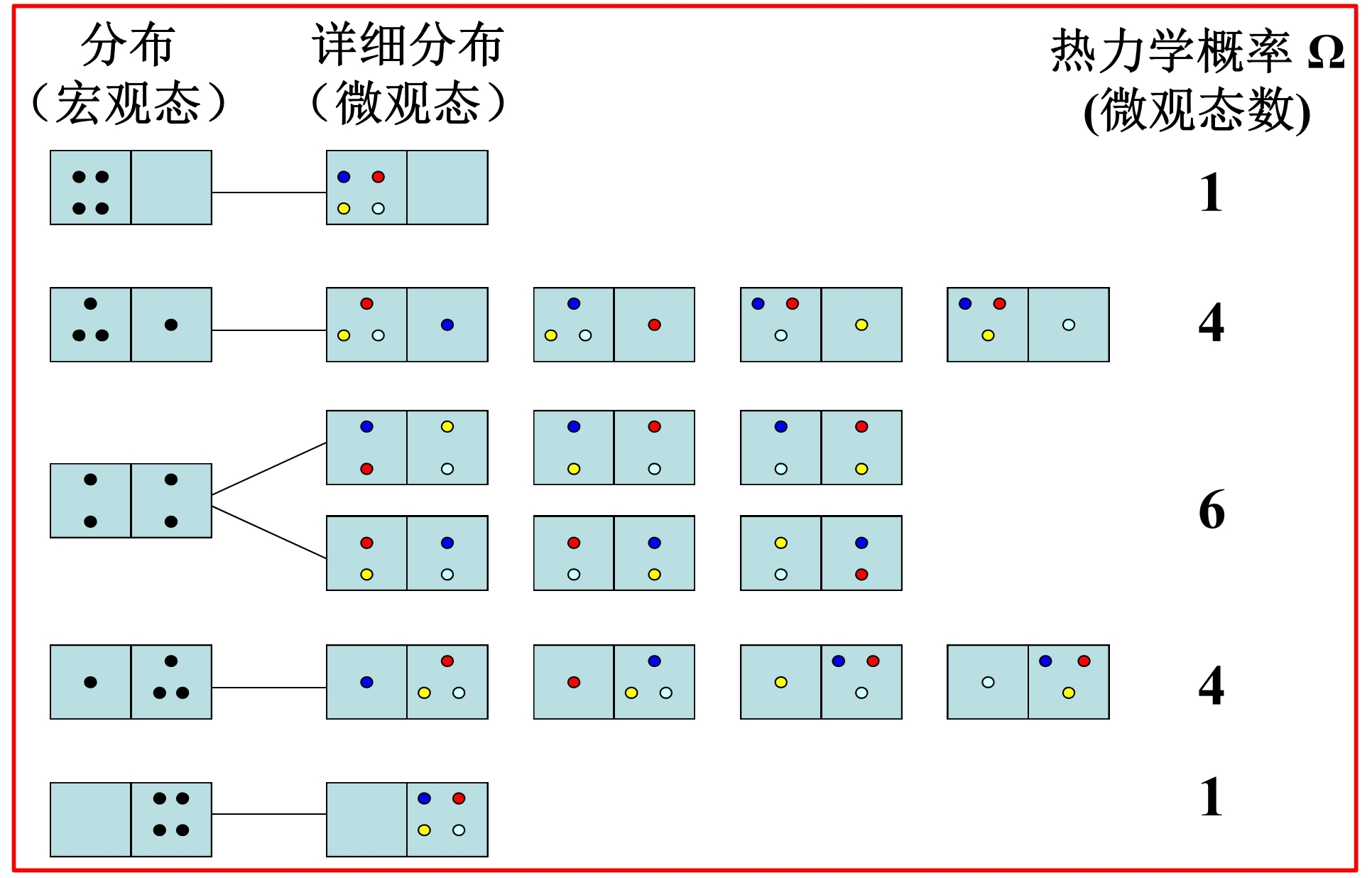其中的状态发生的概率最大，而当足够大时，几乎只可能发生这种情况，故实际观测到的总是均匀分布的这种宏观态，即系统最后所达到的平衡态
热力学第二定律的统计表述
孤立系统内部所发生的过程总是从包含微观态数少的宏观态向包含微观态数多的宏观态过渡，从概率小的状态向概率大的状态过渡.
由此可知
- 平衡态是包含微观态数目最多的宏观态；
- 平衡态是最混乱、最无序的状态；
- 一切自然过程总是沿着无序性增大的方向进行的.
热力学第二定律的适用范围
- 适用于宏观系统的热力学过程，而不适用于由少数粒子组成的微观系统的过程，如布朗运动；
- 热力学孤立系统是有限系统，不可推广到无限的宇宙 (热寂说).
Carnot定理
Carnot定理
- 在相同高温热源和低温热源之间工作的一切可逆热机，其效率都相等，与工作物质无关（）
- 在相同高温热源和低温热源之间工作的一切不可逆热机的效率都不可能大于可逆热机的效率（）
其中的热源都是指温度均匀且恒定不变的热源，若一可逆热机在某一确定温度的热源处吸热，在另一确定热源处放热，从而对外做功，则该可逆热机必然是由两个等温过程和两个绝热过程所组成的可逆Carnot热机；
Carnot定理指出了热机效率的极限和提高热机效率的途径：
- 使热机尽量接近可逆热机；
- 尽量增大两热源的温度差
Carnot定理的推广
任意循环过程的效率，不可能大于工作于它所经历的最高热源温度与最低热源温度之间的可逆Carnot循环的效率
关于制冷机的效能
在相同高温热源和低温热源之间工作的一切可逆制冷机的制冷系数都相等，与工作物质无关
在相同高温热源和低温热源之间工作的一切不可逆制冷机的制冷系数不不可能大于可逆制冷机的制冷系数