热力学第一定律

准静态过程的定义和物理意义

准静态过程满足在过程中的每一个时刻, 系统都可以近似认为处于平衡态

平衡态指没有外界影响, 系统各个参量保持稳定不变的状态
在平衡态中我们可以定义状态函数

准静态过程需要有条件使得整个过程进行得无限缓慢, 可以描述为过程变化的特征时间远大于弛豫时间

特征时间表示过程变化的时间量级
弛豫时间表示从非平衡态达到平衡态需要的时间

准静态过程是一个理想的物理模型, 不可能严格实现. 准静态过程中的每一个时刻都可以用确定的状态参量来描述（因为每一刻都是平衡态）, 它们对应于相图上的一个点, 整个过程就可以表示为相图上的一条有方向的曲线

准静态过程可分为: 等温过程、等压过程、等体过程、绝热过程和循环过程

功、热、内能的定义及它们之间的关系

功是在热力学过程中, 系统和外界环境之间由于力学效应而产生的能量转移

功
- 体积功: 膨胀功, 表示机械能和内能之间的转换
- 非体积功
  - 表面张力功
  - 摩擦功
  - 电功

热量是在热力学过程中, 外界环境与系统之间的由于热学相互作用而产生的能量转移

当系统和外界环境存在温差时, 通过热传导方式发生的能量转移
微观本质: 分子无规则热运动的能量从高温物体向低温物体传递
微元过程中, 外界传递给系统的热量 $d Q = C d T$ , 其中热容 $C$ 依赖于过程, 如定体、定压等

内能的微观定义

一个热力学系统的内能是组成该系统微观粒子无规则热运动的动能和分子之间相互作用的势能的总和；不包含这个系统做整体运动的动能和在外场（如重力场）中的势能
内能还包括化学能、电离能和原子核内部的核能, 但我们考虑的热力学过程一般不涉及化学反应, 物质的原子结构、核结构也不发生变化, 所以可以忽略不计

内能的宏观定义

系统内能的增量等于绝热过程中外界对系统所做的功

内能的性质

功和热是过程量, 而内能是状态函数
特别地, 理想气体的内能只是温度的函数
内能的绝对值并不重要, 我们关心内能的相对变化量
做功和热传递都可以改变内能

内能的具体形式

理想气体的内能 $U = C_{V} T$
Van der Waals气体的内能 $U = \int_{0}^{T} C_{V} d T + U_{0} - \frac{a ν ^{2}}{V}$

热力学第一定律的含义

设经过某一过程（不要求是准静态过程）系统由平衡态 $1$ 变到平衡态 $2$ , 系统内能的增量等于在此过程中外界对系统所传递的热量和外界对系统做功之和

d U = d Q + d W

本质上是能量守恒定律在热力学中的体现

循环过程效率的定义及其计算

循环过程最终会使热力学过程回到初始状态, 循环过程具有两个方向

正循环, 顺时针, 对外做功
逆循环, 逆时针, 做负功

热机

利用从高温热源吸收的热量 $Q_{1}$ 对外做功 $W$
效率 $η = \frac{W}{Q _{1}}$
其中 $Q_{1}$ 满足两个条件: 和高温热源交换、从中吸收的热量

制冷机

利用外界提供的功 $W$ 从低温热源吸收热量 $Q_{2}$
效率 $ε = \frac{Q _{2}}{W}$
其中 $Q_{2}$ 满足两个条件: 和低温热源交换, 从中吸收的热量

Carnot循环是工质只与两个恒温热源交换热量的理想化循环, 其中

与两个恒温热源交换热量的过程: 两个等温过程；
不与其它热源交换热量的过程: 两个绝热过程.

任意工质的卡诺循环在 $T - S$ 图上表示为一个长方形

理想Carnot循环的效率为

η = 1 - \frac{Q _{2}}{Q _{1}} = 1 - \frac{T _{2}}{T _{1}}

由此可知理想气体卡诺热机的效率仅由两个热源的温度决定, 如果想要提高循环效率, 需要提高高温热源的温度和降低低温热源的温度. 而对于实际热机而言, 由于低温热源一般为大气、水等自然环境, 故提高高温热源的温度更加实际, 工作物质的燃烧温度越高, 热机效率也就越高

实际气体焦耳-汤姆孙效应的物理来源

Joule-Thomson 实验

多孔塞: 由多孔物质（如棉絮）做成的装置, 对气流有较大的阻滞作用, 使气体不容易很快通过它, 从而能在两边维持一定的压强差

一个节流过程是指, 压强为 $p_{1}$ 的气体通过多空塞后, 压强将为 $p_{2}$ , 且其温度也有 $T_{1}$ 变为 $T_{2}$

在绝热条件下高压气体经过多孔塞流到低压一边的过程则叫做绝热节流过程

绝热节流过程中的不变量

设在 $Δ t$ 时间内, 有一定量的高压气体通过多孔塞, 状态从 $(p_{1}, V_{1}, T_{1})$ 变成 $(p_{2}, V_{2}, T_{2})$ , 则它对外界的做功为 $p_{2} V_{2} - p_{1} V_{1}$ , 由于过程绝热, 由热力学第一定律有

U_{2} - U_{1} = p_{1} V_{1} - p_{2} V_{2} ⟺ U_{1} + p_{1} V_{1} = U_{2} + p_{2} V_{2}

即

H_{1} = H_{2}

也就是说, 绝热节流过程是等焓过程

J-T 系数

对于理想气体, 焓 $H = C_{p} T$ 只是温度的函数, 所以它在节流过程中温度不发生改变；但是对于实际气体而言, 由于其焓还和压强（体积）有关, 所以它在节流过程前后会有温度的变化, 为了表示在节流膨胀过程后, 随压强的稍许降低而引起的温度变化, 引入J-T系数 $α$

α = (\frac{\partial T}{\partial p})_{H}

在准静态过程中, 考虑焓 $H (T, p)$ 全微分（体积可由状态方程确定, $V = f (T, p)$ ）

d H = (\frac{\partial H}{\partial T})_{p} d T + (\frac{\partial H}{\partial p})_{T} d p

对于等焓过程, 即有

α = (\frac{\partial T}{\partial p})_{H} = - \frac{( \frac{\partial H}{\partial p} ) _{T}}{( \frac{\partial H}{\partial T} ) _{p}} = - \frac{1}{C _{p}} (\frac{\partial H}{\partial p})_{T}

由此我们可以通过测量 $H$ 关于 $p$ 的改变量, 或者直接通过 $H$ 的形式来确定实际气体的 $α$

对于一般临界温度不太低的气体如氮、氧、空气等, 在常温下节流后温度都降低, $α > 0$ , 称为制冷效应（或正效应）；对于临界温度很低的气体如氢气, 在常温下节流温度反而升高, $α < 0$ , 称为负效应.

节流制冷过程可用于气体降温和液化

节流过程是熵增过程

热力学第二定律和第三定律

可逆过程和不可逆过程的定义和物理意义

一个系统由某一状态出发, 经过某一过程后到达另一个状态. 如果存在另一个过程使得系统和外界都完全复原（即系统恢复到原来的状态, 同时消除对外界的一切影响）, 则称原来的过程为可逆过程；反之, 如果用任何方式都不能使系统和外界同时完全复原, 则称原来的过程为不可逆过程.

无摩擦力和其它损失的准静态过程是可逆过程；有摩擦力或其它损失的准静态过程是不可逆过程；而非静态过程是不可逆过程

不可逆因素

耗散不可逆因素: 有摩擦力或其它耗散
力学不可逆因素: 如系统内部各部分之间的压强差不是无穷小
热学不可逆因素: 如系统内部各部分之间的温度差不是无穷小
化学不可逆因素: 如系统内部各部分之间化学成分的差异不是无穷小

可逆过程是一种理想化过程, 实际上并不存在

热力学第二定律的语言表述、物理含义及其数学表述

记忆方法: Clausius的名字首字母是C, 可以令人联想到摄氏度 $^{\circ} C$ , 所以Calusius表述和温度有关

Kelvin表述

不可能从单一热源吸收热量, 使之全部转化为有用的功而不产生其它影响.

其中

单一热源指温度均匀且恒定不变的热源；
其它影响指除了由单一热源吸热, 把所吸收的热用来做功以外的任何其他变化

这说明效率为 $100%$ 的热机是不存在的（在这种情况下 $W = Q_{1} ⟹ η = \frac{W}{Q _{1}} = 0$ ）

Kelvin表述表明了热功转换的不可逆性: 功转化为热可以自发地进行；热转化为功却不能在不对外界产生其它影响的条件下自发地进行

Clausius表述

不可能把热量从低温物体转移到高温物体而不产生其它影响

也就是说制冷系数等于无穷大的制冷机是不可能制造成功的

Calusius表述表明了热传递的不可逆性

两种表述一种是从热机出发, 一种是从制冷机出发；一种表明了热功转化的不可逆性, 一种表明了热传递的不可逆性

两种表述的等价性

若Clausius表述不正确, 则Kelvin表述也不正确: 可以把某一热机向低温热源放的热全部释放到高温热源, 那么就相当于实现了一个只需要一个热源的热机
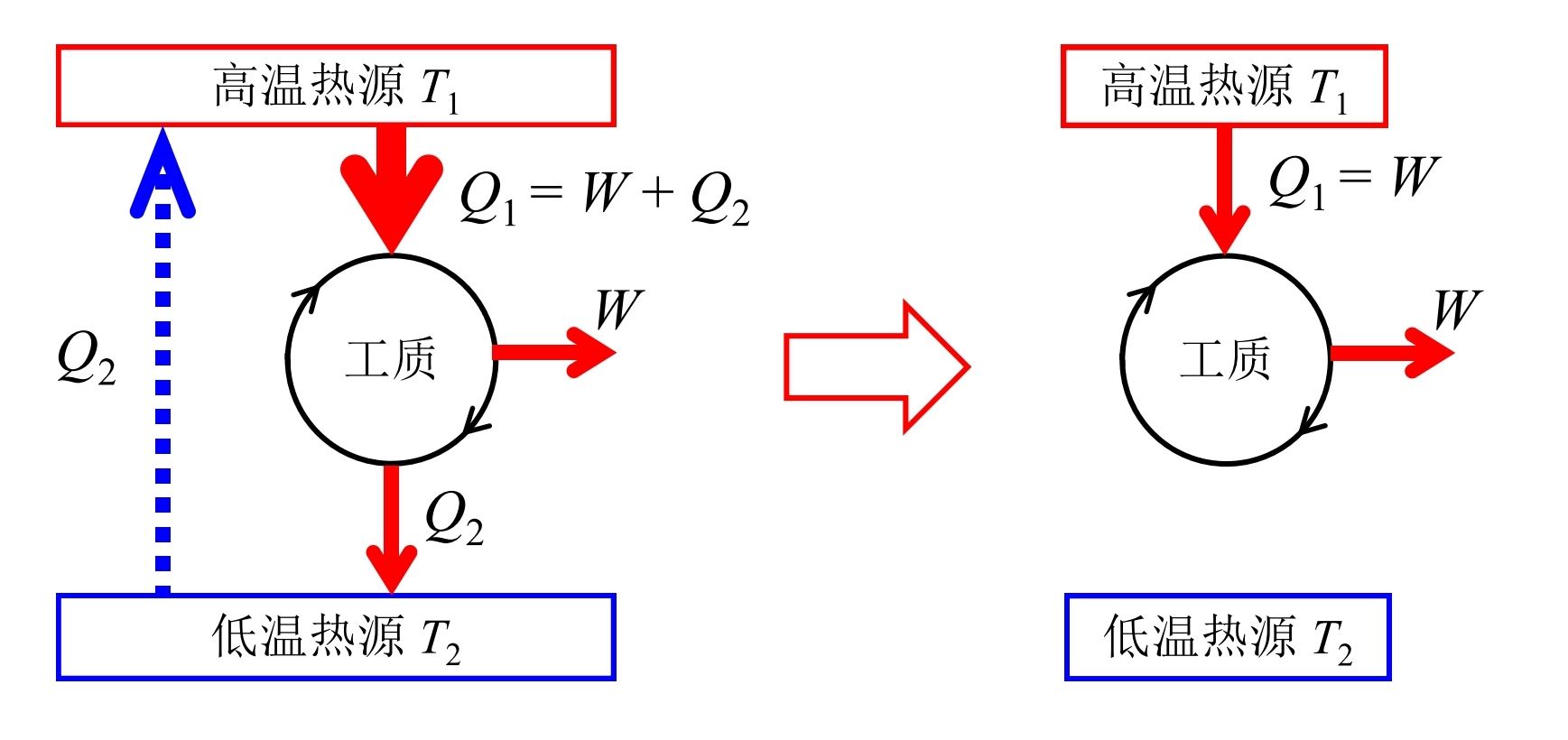
若Kelvin表述不正确, 则Calusius表述也不正确: 如果存在这样一个热机能够从高温热源吸收热量 $W$ 全部转化为功 $W$ 驱动一个制冷机, 这一个制冷剂从低温热源吸取热量 $Q_{2}$ 并向高温热源放出 $W + Q_{2}$ 的热量, 这整体就相当于从低温热源吸收了 $Q_{2}$ 热量并全部传递到了高温热源, 这违反了Calusius表述

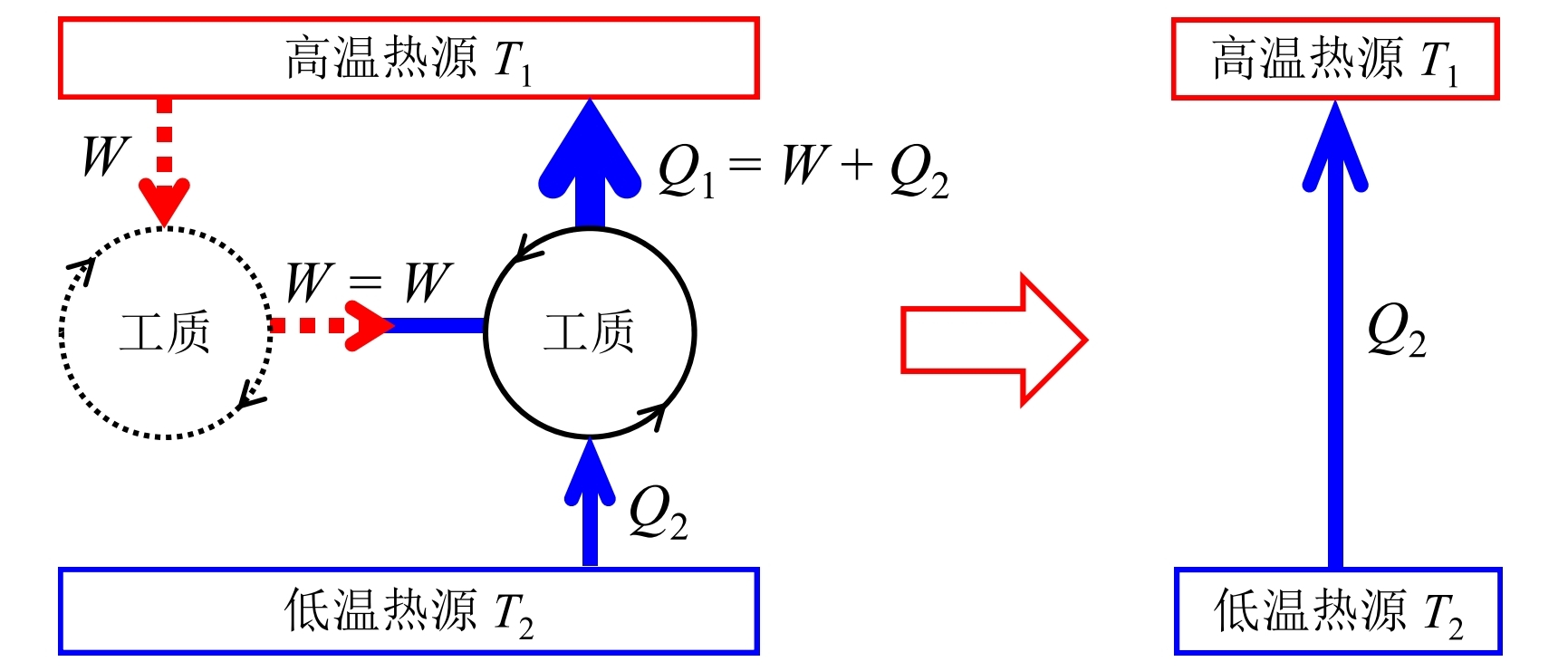
在物理中的实际应用

绝热膨胀是不可逆的

若不然, 则可以设计一个单一热源给予气体热量 $Q$ 令其膨胀做功 $A$ , 而该气体可以自动地在绝热条件下收缩到初态, 这就形成了一个从单一热源吸热做功的第二类永动机

绝热线不能相交

由热力学第二定律可知, $p - V$ 图上的两条绝热线不可能相交, 否则再画一条等温线和这两套绝热线分别相交, 就构成了只有一个热源的循环过程

气体扩散是不可逆的

若不然, 假设均匀混合的气体A,B可以自发地分离, 使得容器左边全为气体A, 容器右边全为气体B, 那么我们可以在两种气体的分界面处设置两个连接外部做功装置的半透膜活塞, 靠左边的半透膜活塞只允许A气体的分子通过, 靠右边的半透膜活塞只允许B气体的分子通过. 这时如果外部热源为气体A,B的分子提供穿越半透膜膨胀的能量, 那么A气体将穿过左边的半透膜活塞推动右边的半透膜活塞对外做功, 直到其膨胀至占满整个容器；B气体将穿过右边的半透膜活塞推动左边的半透膜活塞对外做功, 直到其膨胀至占满整个容器, 最后又回到两种气体均匀混合的初始状态.

而这就形成了一个从单一热源吸热做功的系统

熵的宏观定义

Clausius不等式

对于任意循环过程, 热温比的总和小于等于 $0$

\oint \frac{d Q}{T} \leq 0

当循环过程可逆时取等号, 此时为Calusius等式, 取不等号时为Calusius不等式

热温比的积分

对于一个可逆的循环过程, 其热温比的积分

\int_{i}^{t} \frac{d Q}{T}

和路径无关, 故我们可以定义对于的势能（状态函数）, 称为熵 $S$ 使得

S_{t} - S_{i} = \int_{i}^{t} \frac{d Q}{T}

这就是熵的宏观定义

熵变计算

由此可以计算熵变, 利用热力学第一定律

d Q = d U + p d V = C_{V} d T + (\frac{\partial U}{\partial V})_{T} d V + p d V

和内能公式

(\frac{\partial U}{\partial V})_{T} = T (\frac{\partial p}{\partial T})_{V} - p

我们可以推出

Δ S = \int_{i}^{t} [\frac{C _{V}}{T} d T + (\frac{\partial p}{\partial T})_{V} d V]

对于理想气体

p V = ν RT ⟹ (\frac{\partial p}{\partial T})_{V} = \frac{ν R}{V}

于是

Δ S = \int_{(T_{0}, V_{0})}^{(T_{1}, V_{1})} [C_{V} \frac{d T}{T} + ν R \frac{d V}{V}] = C_{V} ln \frac{T}{T _{0}} + ν R ln \frac{V}{V _{0}}

熵增加原理

对于一般过程, 有

Δ S = S_{t} - S_{i} \geq \int_{i}^{t} \frac{d Q}{T}

考虑绝热过程, 有 $d Q = 0$ , 故此时 $Δ S \geq 0$

熵增加原理

当热力学系统从一平衡态经绝热过程到达另一个平衡态时, 它的熵永不减少. 如果过程是可逆的, 则其熵不变；如果过程是不可逆的, 则其熵增加

熵增加原理只适用于绝热过程, 不适用于其它过程；熵增加原理只适用于孤立系统, 不适用于开放系统；
如果一个准静态过程可逆但是不绝热, 该过程中系统的熵可以增加、减少, 也可以不变；
熵增加原理是孤立系统中绝热过程是否可逆的判据；
熵增加原理是孤立系统中绝热过程自发进行方向的判据；
熵增加原理是热力学第二定律在孤立系统中的一种表述.

Clausius不等式 vs 熵增加原理

Calusius描述的是对于任意循环过程, 其回到原状态后, 热温比的和也就是熵变始终大于等于零

熵增加原理表述的是对于任意绝热过程（不需要回到原点）, 过程中系统的熵变也始终大于等于零

二者都在过程可逆的时候熵变取零

Carnot定理和热力学第二定律的关系

Carnot定理

在相同高温热源 $T_{1}$ 和低温热源 $T_{2}$ 之间工作的一切可逆热机, 其效率都相等, 与工作物质无关（ $η = 1 - \frac{T _{2}}{T _{1}}$ ）

在相同高温热源 $T_{1}$ 和低温热源 $T_{2}$ 之间工作的一切不可逆热机的效率都不可能大于可逆热机的效率（ $η \leq 1 - \frac{T _{2}}{T _{1}}$ ）

其中的热源都是指温度均匀且恒定不变的热源, 若一可逆热机在某一确定温度的热源处吸热, 在另一确定热源处放热, 从而对外做功, 则该可逆热机必然是由两个等温过程和两个绝热过程所组成的可逆Carnot热机；

Carnot定理的推广就是Clausius不等式, 而在定义了熵变之后由Clausius不等式可以导出熵增加原理, 熵增加原理和热力学第二定律是等价的

热力学温标的建立

回忆Carnot定理, 工作于两个恒温热源之间的可逆热机, 其效率只跟热源的温度有关, 而与工作物质或所做的功的大小无关；故其效率是两个温度 $θ_{1}, θ_{2}$ 的普适函数, 而和过程中的热量交换及工质无关

η = 1 - \frac{Q _{2}}{Q _{1}} ⟹ \frac{Q _{2}}{Q _{1}} = 1 - η = f (θ_{1}, θ_{2})

这时候我们构造一个热机是两个热机的和

M1 : Q_{1} \to Q_{2} + W_{1}, M2 : Q_{3} \to Q_{1} + W_{2} M3 = M1 + M2 : Q_{3} \to Q_{2} + (W_{1} + W_{2})

分别考虑它们的效率

1 - η_{1} = \frac{Q _{2}}{Q _{1}} = f (θ_{1}, θ_{2}), 1 - η_{2} = \frac{Q _{1}}{Q _{3}} = f (θ_{3}, θ_{1})

和

1 - η_{3} = \frac{Q _{2}}{Q _{3}} = f (θ_{3}, θ_{2})

故

\frac{Q _{2}}{Q _{1}} = \frac{Q _{2}}{Q _{3}} / \frac{Q _{1}}{Q _{3}} ⟹ f (θ_{1}, θ_{2}) = \frac{f ( θ _{3} , θ _{2} )}{f ( θ _{3} , θ _{1} )}

由于 $θ_{3}$ 是独立的, 所以 $f$ 必须有 $\frac{Q _{2}}{Q _{1}} = f (θ_{1}, θ_{2}) = \frac{ψ ( θ _{1} )}{ψ ( θ _{2} )}$ 的形式, 我们可以用这个关系来标定温度: 假设我们已经知道某个热源的温度, 热力学温标 $ψ (θ_{0})$ , 那么我们构建一个工作在这个已知温度和待测量温度之间的一个Carnot热机, 就可以通过上式确定待测量温度的热力学温标 $ψ (θ_{1})$

热力学第三定律

Nernst 定理

实验观察发现, 凝聚系的熵在等温过程中的改变在当这个过程的温度趋于绝对零度时趋于 $0$ , 即凝聚系在绝对零度进行的任何热力学过程中熵保持不变.

等温条件下化学反应的Gibbs自由能变 $Δ G$ 和焓变 $Δ H$ 随着温度逐渐趋于 $0$ 而趋于 $0$

而对等温过程有

G = H - TS ⟹ Δ G = Δ H - T Δ S

于是

T \to 0 lim \frac{\partial ( Δ G - Δ H ) _{T}}{\partial T} = T \to 0 lim \frac{\partial T ( Δ S ) _{T}}{\partial T} = 0 ⟹ T \to 0 lim (Δ S)_{T} = 0

即为Nernst定理

绝对零度不能达到定理

Nernst根据他的定理提出了绝对零度不能达到原理: 不可能通过有限多的步骤使得物体温度降低到绝对零度

在绝对零度时, 等温线与等熵线 (绝热线) 重合, 又因为两条绝热线不相交, 所以不可能通过可逆绝热过程使一个物体从 $T \neq = 0 K$ 的状态达到绝对零度

绝对零度不能达到原理和Nernst定理是等效的, 它们是热力第三定律的两种不同表达

液体

液体的微观结构

有序性

液体是介于气态和固态的一种物态, 液体分子间距小, 分子力大, 不易被压缩；液体分子的排列存在一定的有序性.

在靠近液体每一个分子的周围, 其它分子的分布在一定程度上是有序的, 液体中分子分布的有序较为松散. 因而, 液体的结构即不同于固体的长程有序, 也不同于气体的无序, 表现为短程有序、长程无序

液体中存在一个个局部有序区域, 我们称其为类晶区

理论描述

为了定量地描述液体的微观结果, 我们定义径向分布函数 $g (r)$ 为包含在 $r \sim r + d r$ 球形球壳内的平均分子数分布

g (r) = 4 π r^{2} ρ (r)

其中径向密度 $ρ (r)$ 定义为 $r \sim r + d r$ 球形壳层内的平均分子数密度

下图是水分子的径向分布函数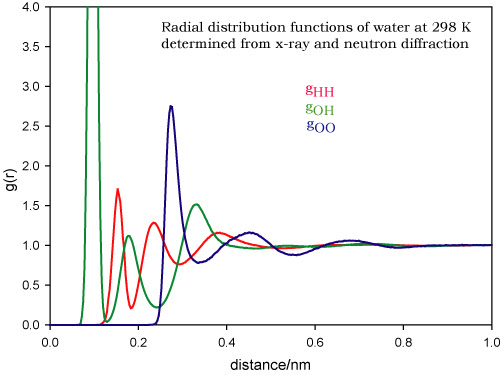可见在距离较大时, 径向密度趋于一条水平线, 说明液体确实和气体一样长程无序；而在距离较小时, 径向密度的规律起伏可以说明起短程有序性

当温度升高时, 液体的径向分布函数趋近于气体的径向分布函数（近似于一条直线）；当温度降低时, 液体的径向分布函数趋近于相对应固体的径向分布函数

液体分子的热运动

热运动模式

液体分子间的平均距离与固体相当, 分子间的相互作用很大；液体分子的热运动与固体相近, 主要是在其平衡位置附近振动（热振动）.

热运动特点

液体分子的排列不很规则, 分子间相互作用势阱的形状、深度各不相同；同一势阱里（类晶区）粒子的振动模式基本一致；不同势阱里粒子的振动模式各不相同；
势阱的形状随时间改变；故粒子振动的中心和相应的振动时间不确定, 具有“游牧生活”的特点, “迁移”和“定居”交替.

定居时间

液体分子的定居时间（residence time）, 通常表示为 $𝜏$ , 是指液体分子在某个特定区域内（如在某个体积元素或在溶液中的某个位置）停留的平均时间. 其大小由分子间相互作用和热运动的竞争决定.

外力作用下的行为

非晶体的微观结构与液体非常类同, 可以认为它是一种没有流动性（ $τ \to \infty$ ）的液体. 外力作用于非晶体的时间总是小于 $τ$ , 所以在外力作用不会流动, 而发生弹性形变、脆性断裂等力学现象；

对一般液体, 当外力作用时间大于定居时间 $τ$ 时, 分子在该时间内可以有很大的移动, 故液体将在外力作用下流动；而当外力作用时间远小于液体 $τ$ 时, 液体也会发生弹性形变甚至断裂； **在非常强的冲击力下, 液体会像玻璃那样碎裂. **

表面张力系数的物理含义

表面张力系数

表面张力与液面相切、与线段垂直且指向其两侧, 可分别用 $F$ 和 $F^{'}$ 表示, 它们是一对作用力和反作用力

由于线段上各点均有表面张力作用, 故线段越长, 表面张力越大, 有

F = γ L

其中 $γ$ 为表面张力系数

表面功

d W = γ d A

在绝热条件下, 由热力学第一定律

d U = d W = γ d A ⟹ γ = (\frac{\partial U}{\partial A})_{绝热}

此时表面张力系数是绝热条件下增加单位表面时所增加的表面内能, 即单位表面的表面内能

对于表面系统的可逆等温过程, 由自由能的定义

d F = d W = γ d A ⟹ γ = (\frac{\partial F}{\partial A})_{等温}

此时表面张力系数是等温条件下增加单位表面时所增加的表面自由能, 即单位表面的表面自由能

在外界不对系统做功时, 等温情况下, 表面自由能减少直到取到最小值, 而球形的表面积最小, 所以不受任何合外力作用的液体呈球体形状

影响表面张力系数的因素

液体成分: 密度小、容易挥发的液体 (如液氢和液氦) $γ$ 较小, 而金属熔液的 $γ$ 则很大；
温度: 温度越高, $γ$ 越小, 实验表明可近似为一线性关系
表面(即第二介质)性质: 两种互不相溶液体表面的 $γ$ 与这两种液体的成分有关；
杂质: 加入杂质能显著改变液体的 $γ$ , 其中使 $γ$ 减小的杂质称为表面活性物质 如肥皂水, 醇、酸、醛、酮等有机物质.

表面张力的微观解释

液体分子之间存在Van der Waals力（包括London色散力、偶极-偶极相互作用和氢键等）. 在液体内部, 每个分子受到来自周围各个方向的分子引力, 这些力相互抵消, 导致分子在液体内部处于平衡状态.

然而, 在液体的表面层, 分子上方没有液体分子, 只有空气分子或真空. 因此, 表面分子受到的净引力是指向液体内部的. **这种不平衡的力使得表面分子向内拉, 从而使液体表面趋向最小化其表面积. **

拉普拉斯公式

如果液面不是平面, 液面两边会因为表面张力的作用而产生压强差

Δ p = p_{内} - p_{外} = γ (\frac{1}{R _{1}} + \frac{1}{R _{2}})

其中 $R_{1}, R_{2}$ 是表面上这一点任意两个相互垂直的截口的曲率半径.

提示

对于如肥皂泡这种液面足够薄且两端都是表面的情况, 上面的压强差还需要乘以 $2$

数学上可以证明任意一对相互垂直的正截口的曲率之和都相等, 即 $\frac{1}{R _{1}} + \frac{1}{R _{2}} = const$

毛细现象

将毛细管插入液体中, 管内液面相对于管外液面上升或下降的现象称为毛细现象.

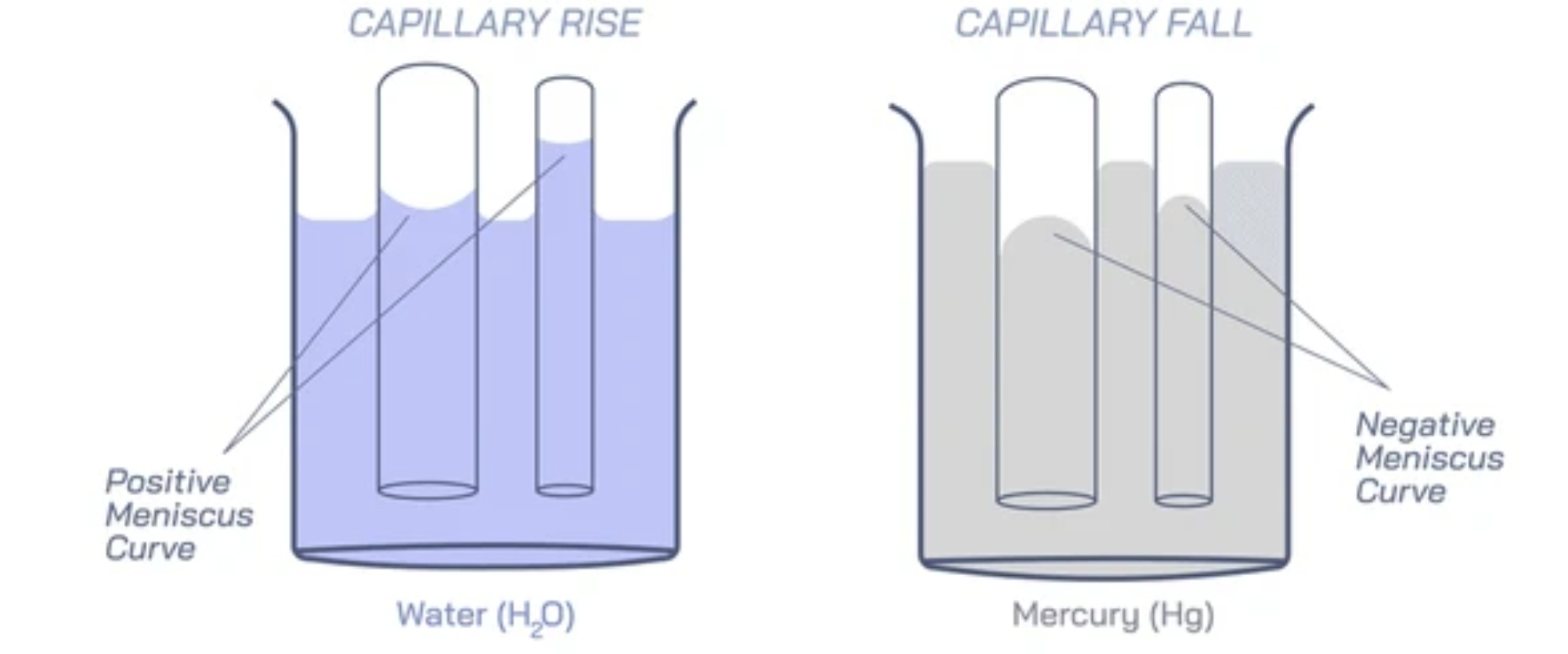
物理解释

内聚力与附着力的竞争引起液面弯曲, 弯曲液面内外的压强差导致的管内液体上升或下降.

附着力大于内聚力, 液体湿润固体, 液面下凹: 液面内压强小于液面外压强, 毛细管内液面上升；
附着力小于内聚力, 液体不湿润固体, 液面上凸: 液面内压强大于液面外压强, 毛细管内液面下降.

液柱高度的计算

液柱表面两边的压强差 $=$ 液柱产生的压强, 则有

γ (\frac{1}{R _{1}} + \frac{1}{R _{2}}) = ρ g h

如果是半径为 $r$ 的毛细管, 凹液面的两个曲率半径 $R_{1} = R_{2} = \frac{r}{cos θ}$ , 于是便有

h = \frac{2 γ cos θ}{r g ρ}

如果是相隔为 $d$ 的平行板, 则有 $R_{1} = \frac{d}{2 cos θ}, R_{2} = + \infty$ , 于是便有

h = \frac{2 γ cos θ}{d g ρ}

相变

相和相变的定义

物态

大量的微观粒子在一定的热力学状态(温度和压强)下相互聚集为一种稳定的结构状态, 这种状态就是“物质的一种状态”, 简称物态

相

热力学平衡态下, 物理、化学性质完全相同的均匀物质的聚集态称为物质的一个相, 即系统中物理、化学性质均匀的部分, 它和其它部分之间有一定的分界面隔离开来

几点说明:

物态是物质(系统)的一个平衡态, 但不一定是均匀的
一个物态中可能存在多个相, 即多相共存；
一个相是均匀的, 但不一定是一种化学成分
相与相之间有分界面, 可以通过物理或机械的办法分开

也就是说

单元均匀系 \subset 相 (多元同相) \subset 物态

举例

冰水混合物为系统的一个物态, 其中冰和水是两个不同的相, 故系统是一个单元复相系；
酒精溶于水, 酒精和水的混合物为一相, 故系统是一个多元单相系；
气体或气体混合物一般只有一个相, 即气相；
对于固体, 不同点阵结构的物理性质不同, 分属不同的相.

凝聚态

凝聚态物质指的是原子或分子间具有较强相互作用力, 使得物质呈现出较为固定的结构和形态. 主要包括固态、液态、玻璃态、超流态等等

非凝聚态

非凝聚态物质的原子或分子间相互作用力较弱, 物质的结构较为松散, 主要有气态和等离子态等

相变

相变: 在一定条件下物质从一种相转变为另一种相的变化过程, 即系统的物质结构发生变化的过程称为相变, 相变可以分为两类

狭义相变: 过程前后系统的化学组成不变, 即不发生化学反应；
广义相变: 包括过程前后化学组成的变化；

当压强确定时, 相变是在一个确定的温度下发生的；当温度确定时, 相变是在一个确定的压强下发生的；在相变点(确定温度和压强)处系统可多相共存, 为复相系.

相图

在一个相图中每一个点都代表一个相, 一般而言一个相是连续的, 也就是说一个相点周围的任何一个相点都代表同一个相 $P (p_{0}, T_{0}) = P (p_{0} + d p, T_{0} + d T)$ . 而相变就发生在相点不连续的地方, 通常是相图上一些曲线的集合. 在这些曲线上可以实现多相共存

相变是大量粒子相互作用的结果, 是宏观集体现象；在相变的过程中, 系统的物理特征参量发生不连续变化, 即突变（但是参量的导数可以不连续）

相变的本质是有序和无序两种倾向的竞争: 相变是由构成系统的微观粒子之间的相互作用（倾向于使系统有序）与微观粒子本身的热运动（使系统无序）相互竞争的结果

复相平衡的概念和内容

开放系统的化学势和热力学方程

开放系统即可以与环境交换物质和能量的系统

开放系统与环境仍然可以达到平衡态. 因为系统的物质的量不确定, 对该平衡态的描述需要引入一个新的热力学参量, 即化学势.

化学势 $μ$ 与物质的量（摩尔数 $ν$ ）构成共轭的热力学参量

开放系统的热力学微分方程: 对于一个开放系统, 除传热和做功可引起系统内能改变外, 物质的量的变化也将导致内能的改变

d U = T d S - p d V + μ d ν d H = T d S + V d p + μ d ν d F = - S d T - p d V + μ d ν d G = - S d T + V d p + μ d ν ⟹ μ = ⎩ ⎨ ⎧ (\partial U / \partial ν)_{S, V} (\partial H / \partial ν)_{S, p} (\partial F / \partial ν)_{T, V} (\partial G / \partial ν)_{T, p}

化学势

考虑一等温等压的物质增加过程, 可知

μ = \frac{G ( T , p , ν )}{ν} = G_{m} (T, p) = U_{m} + p V_{m} - T S_{m}

即化学势是等温等压条件下 1 mol 物质的自由焓 同理

化学势是等温等体条件下 1 mol 物质的自由能；
化学势是等熵等压条件下 1 mol 物质的焓；
化学势是等熵等体条件下 1 mol 物质的内能

d μ = d G_{m} (T, p) = - S_{m} d T + V_{m} d p

相平衡条件

设 $1$ 和 $2$ 是一个单元系的已经达到平衡的任意两个相, 且这两个相构成一个孤立系统, 则系统的总内能 $U_{1} + U_{2}$ 、总体积 $V_{1} + V_{2}$ 和物质的量 $ν_{1} + ν_{2}$ 都守恒.

设想“ $1$ ”相和“ $2$ ”相发生了一个无穷小的变动, 由孤立系统的条件有

d U_{1} + d U_{2} = d V_{1} + d V_{2} = d ν_{1} + d ν_{2} = 0

该变化过程中, “ $1$ ”相和“ $2$ ”相单独形成一个开放系统, 由其热力学微分方程可得

d S_{1} = \frac{1}{T _{1}} (d U_{1} + p_{1} d V_{1} - μ_{1} d ν_{1}) d S_{2} = \frac{1}{T _{2}} (d U_{2} + p_{2} d V_{2} - μ_{2} d ν_{2})

系统的总熵变

由孤立系统热平衡条件可知, 当“1”相和“2”相间达到平衡时, 系统总的熵有极大值, 即

d S = (\frac{1}{T _{1}} - \frac{1}{T _{2}}) d U_{1} + (\frac{p _{1}}{T _{1}} - \frac{p _{2}}{T _{2}}) d V_{1} - (\frac{μ _{1}}{T _{1}} - \frac{μ _{2}}{T _{2}}) d ν_{1} = 0

由于 $d U, d V, d ν$ 独立改变, 所以两相平衡的条件为

热学平衡 $T_{1} = T_{2}$
力学平衡 $p_{1} = p_{2}$
化学平衡 $μ_{1} = μ_{2}$

相平衡条件不满足时, 系统中过程进行的方向

热学平衡不满足时, 热量从高温相传递到低温相
力学平衡不满足时, 则压强大的相膨胀, 而压强小的相将收缩；
化学平衡不满足时, 物质从化学势高的相向化学势低的相转移.

一级、二级相变的基本特征和描述方程

相变分类

化学势导数的连续性可对相变的类型分类

一级相变: 相变处两相的化学势相等, 但它们的一阶导数不相等；即在相变处, 系统的化学势连续, 但其一阶导数不连续；
二级相变: 相变处系统的化学势及其一阶导数连续, 但其二阶导数不连续
$K (K > 2)$ 级相变: 相变处, 系统的化学势及其 $k (k = 1, 2, \dots, K - 1)$ 阶导数连续

通常把二级及二级以上的相变统称为连续相变

另一种相演化: 热力学函数及其任意阶偏导数都连续的相演化过程(非相变) 称为连续过渡 (Crossover)

相和相变的另一种理解

相: 系统化学势在热力学状态空间中为解析函数 (任意阶导数都连续, 没有突变) 的物理状态；
相变: 系统化学势出现非解析的点, 即其导数出现不连续或发散.

一级相变

体积跃变和相变功

由化学势的定义

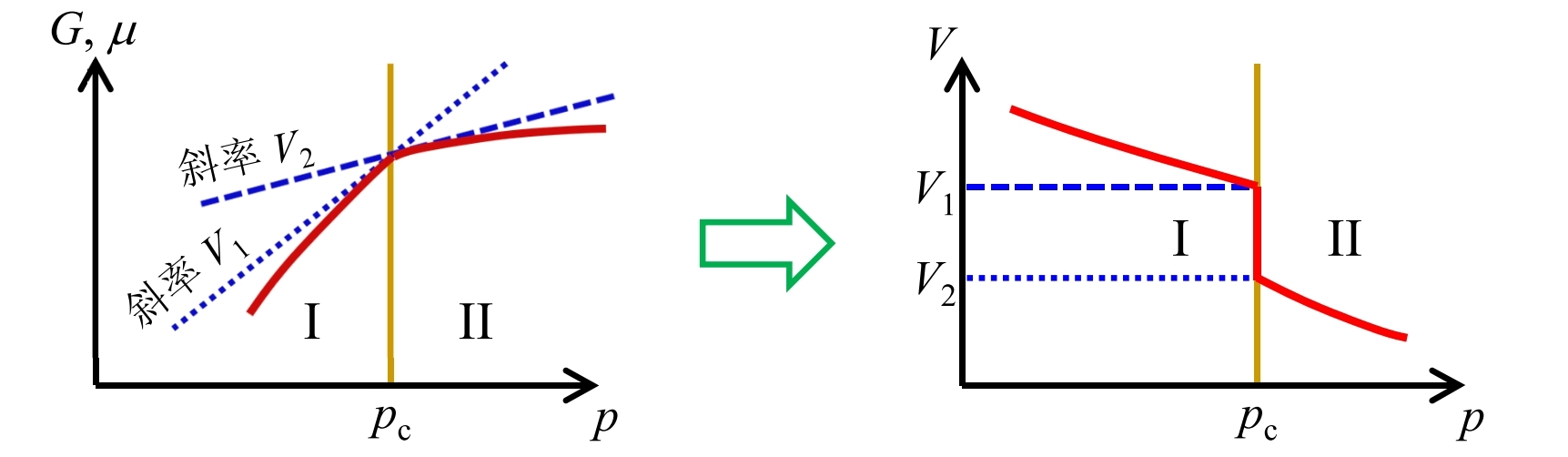(\frac{\partial μ _{1}}{\partial p})_{T} \neq = (\frac{\partial μ _{2}}{\partial p})_{T} ⟹ V_{m 1} \neq = V_{m 2}

所以一级相变过程中, 存在相变功 $W = p (V_{2} - V_{1}) \neq = 0$

相变潜热

(\frac{\partial μ _{1}}{\partial T})_{T} \neq = (\frac{\partial μ _{2}}{\partial T})_{T} ⟹ S_{m 1} \neq = S_{m 2}

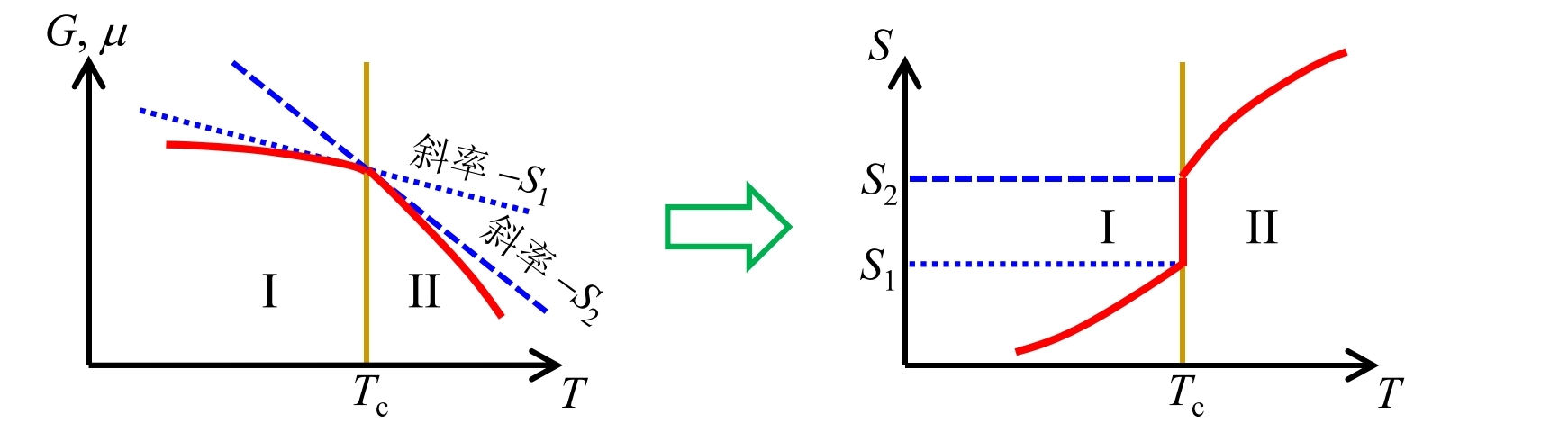定义相变潜热

1 atm下, 1 kg 0 $^{\circ} C$ 的冰要吸收 79.6 kcal 的热量才能转变为同温度的水, 1 kg 100 $^{\circ} C$ 的水要吸收539 kcal的热量才能转变成同温度的水蒸气, 它们分别对应固液相变和液气相变的相变潜热

Clapeyron方程

由单元系的复相平衡条件得到的一级相变相平衡曲线的斜率与相变温度、潜热和两相摩尔体积差之间的关系称为Clapeyron方程

沿一相平衡曲线把系统的温度和压强从 $T, p \to T + d T, p + d p$

μ_{1} (T, p) μ_{1} (T + d T, p + d p) ⟹ d μ_{1} (T, p) = μ_{2} (T, p) = μ_{2} (T + d T, p + d p) = d μ_{2} (T, p)

利用 $d μ = - S_{m} d T + V_{m} d p$ , 可得

\frac{d p}{d T} = \frac{S _{m 2} - S _{m 1}}{V _{m 2} - V _{m 1}} = \frac{L _{m}}{T ( V _{m 2} - V _{m 1} )}

其中 $L_{m} = T (S_{m 2} - S_{m 1})$ 为平衡相变中的摩尔潜热

注意

Clapeyron方程描述的是相平衡曲线的性质, 它描述的是一种平衡状态, 而不是相变过程

相变举例

一级相变: 固液、固气及液气相变, 固-固相变.
二级相变: 铁磁-顺磁相变, 液氦的正常液相到超流相的相变, 超导体的正常态到超导态
连续过渡: BCS-BEC crossover: 微观原子核的不定轴转动到定轴转动之间的演化, 系统的宏观性质没有突变, 仅转动轴的取向发生了变化.

麦克斯韦等面积法则的物理意义

气液等温相变

将 $1 mol$ 某种实际气体装入一封闭气缸, 把气缸置于温度为 $T$ 的恒温热源中, 对他进行等温压缩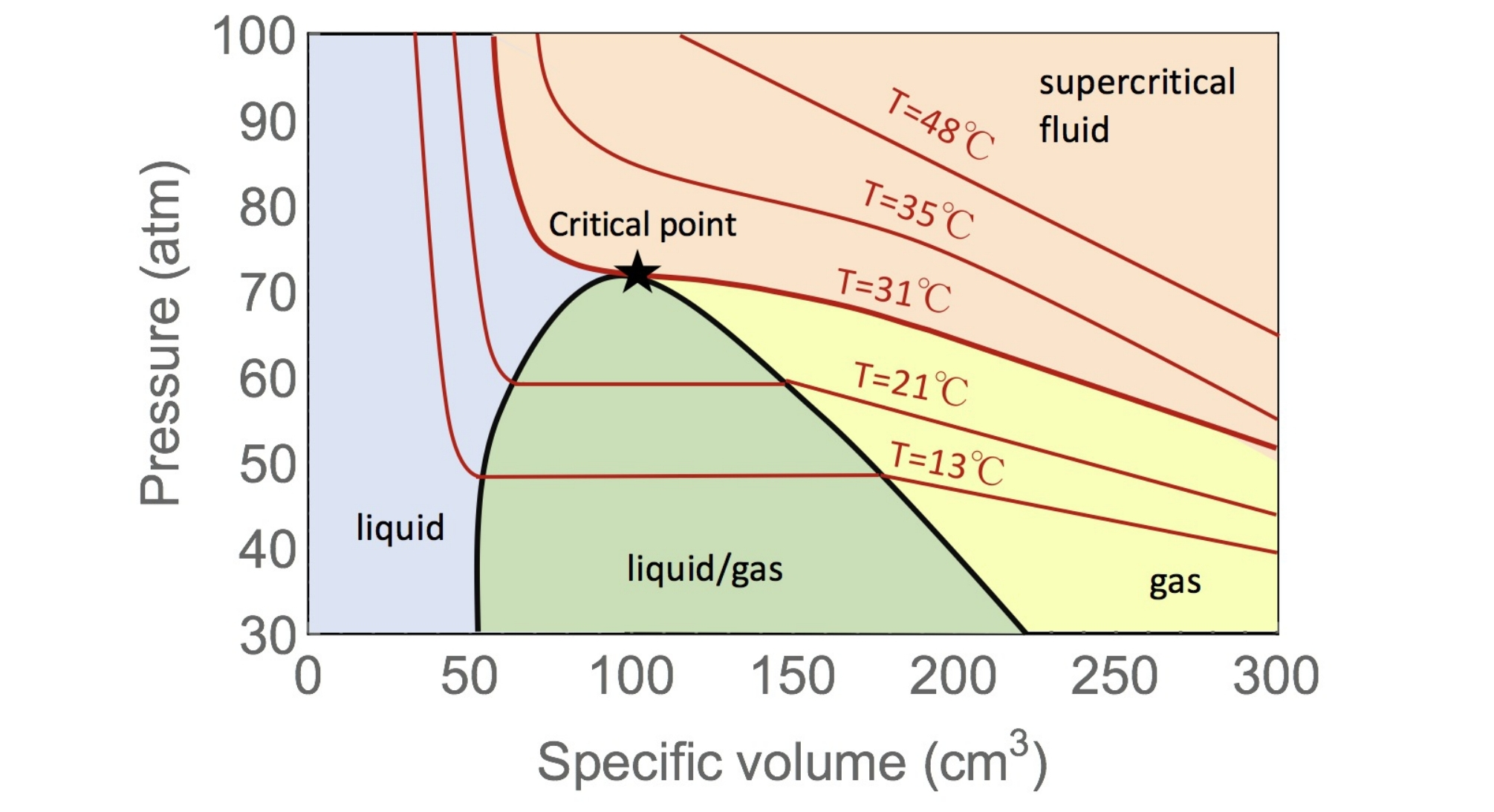上图是 $C O_{2}$ 的等温相变图, 可以看出在温度较低（ $T = 1 3^{\circ} C$ ）时, 过程可以分为三个阶段

气态, 压强随着体积减小而增大
气液共存区, 对系统的压缩不会导致升压, 压强为饱和蒸气压；在此过程中, 饱和蒸汽逐渐被压缩成同温同压的液体
液态, 由于液体的等温压缩系数小曲线更为陡峭

而当温度大于临界温度（ $T_{c}$ ）时, 就不存在相变和两相共存现象, 此时气体无法液化. 临界现象的表现是: 气液不分, 液面消失

临界乳光现象: 在临界状态下, 液相和气相之间频繁交换分子, 使得光在其上的散射增强, 原来透明的气体或液体变得浑浊起来, 呈现一片乳白色的现象, 是临界现象的典型特征

Van der Waals等温线

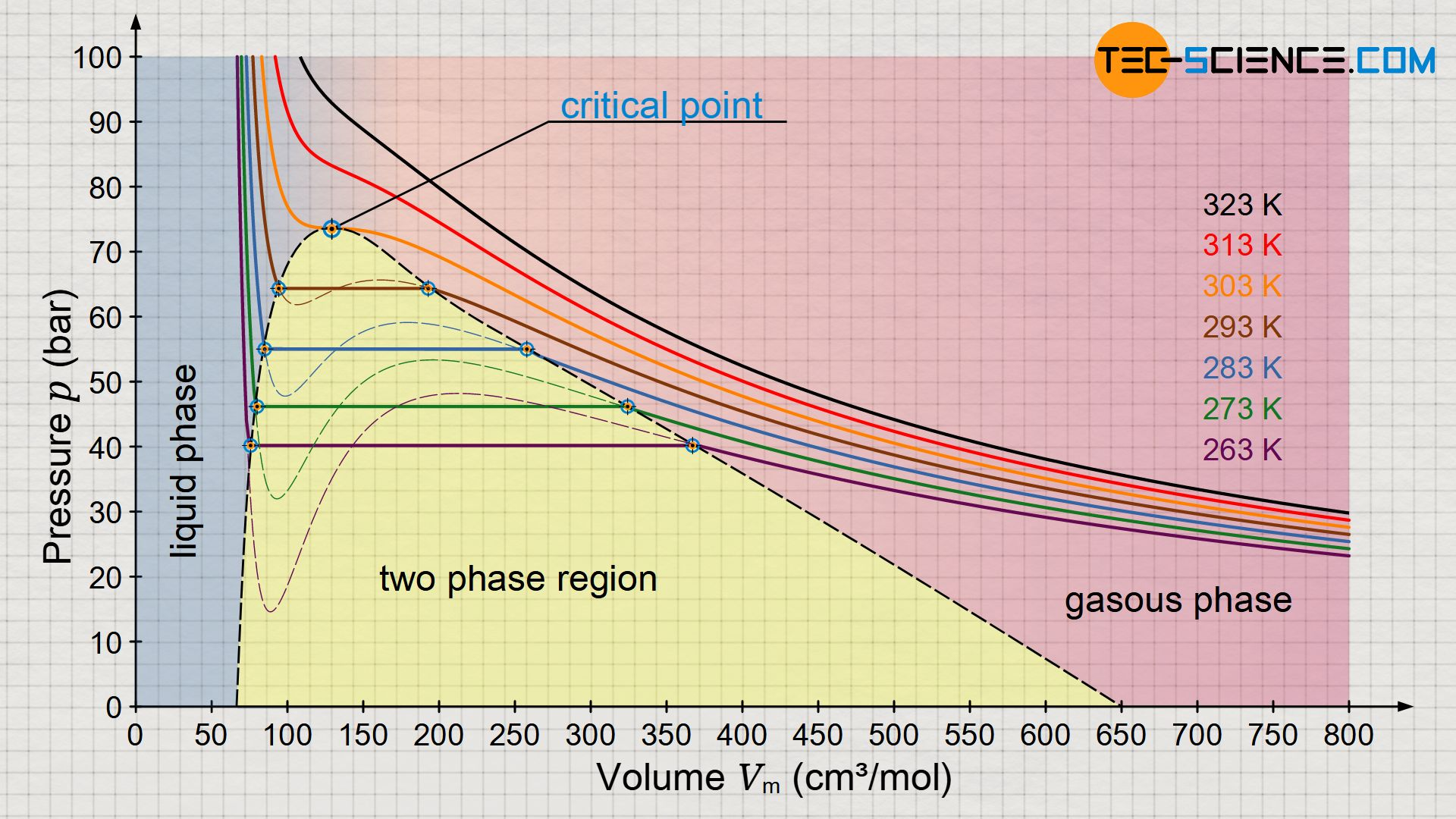即曲线

(p + \frac{a}{V _{m}^{2}}) (V_{m} - b) = RT

可以观察到

温度越高, Van der Waals等温线越接近理想气体等温线
温度在临界温度之上时, 压强是体积的单调递减函数；在临界温度之下时, 压强不再是体积的单调递减函数

极值轨道

等温线上压强取极值的点 $(\frac{\partial p}{\partial V _{m}} = 0)$ 连成的线称为极值轨道, 可计算其方程为

(\frac{\partial p}{\partial V _{m}})_{extreme} = 0 ⟹ p_{extreme} V_{m, extreme} = a (V_{m, extreme} - 2 b)

简记下标 $extreme$ 为 $e$ , 则有

\frac{\partial ^{2} p}{\partial V _{m}^{2}}_{e} = \frac{RT}{V _{m, e}} \frac{( 3 b - V _{m, e} )}{( V _{m, e} - b ) ^{3}}

极值轨道上的拐点, 即极小和极大值的交接点, 就是临界点, 令上面算出的一阶和二阶导数均为 $0$ , 则可得

V_{m, c} = 3 b, p_{c} = \frac{a}{27 b ^{2}}, T_{c} = \frac{8 a}{27 R b}

Van der Waals方程的不足

在低温区会导致负压, 在 $T = 0$ 时达到最低值 $p_{min} = - \frac{a}{b ^{2}}$
无法描述气液共存时压强不变的情况
等温曲线存在斜率为正的线段, 这表明压缩系数 $κ_{T} = - \frac{1}{V} (\frac{\partial V}{\partial p})_{T} < 0$ , 即系统是不稳定的

正压区的方程

为了更好地描述气液共存的状态, 我们可以对Van der Waals等温线作出修正, 使得在气液共存时用一条等压线代替本来的等温曲线

此时有Maxwell等面积法则: 我们需要画的那一条等压线需要满足其和上方曲线围成的面积与其和下方曲线围成的面积相等

气液共存时两相的物质的量之间的关系

记系统总的物质的量为 $ν$ , 两相平衡时系统的摩尔体积为 $V_{m}$ , 定义两相的摩尔密度

x_{liq} = \frac{ν _{liq}}{ν}, x_{gas} = \frac{ν _{gas}}{ν}

于是有

{x_{liq} + x_{gas} = 1 x_{liq} V_{m, liq} + x_{gas} V_{m, gas} = V_{m}

可以解得

x_{liq} = \frac{V _{m, gas} - V _{m}}{V _{m, gas} - V _{m, liq}}, x_{liq} = \frac{V _{m} - V _{m, liq}}{V _{m, gas} - V _{m, liq}}

由此得到系统的总自由能为

F = x_{gas} F_{gas} + x_{liq} F_{liq}

过冷蒸汽和过热液体

在上图的Van der Waals等温线中, BCD段上任意点的等温压缩系数为负数, 是热力学系统的不稳定状态, 在实验中不可能观测到

我们设通过Maxwell等面积法则确定的直线和Van der Waals等温线的交点分别为A和E, 我们发现AB和DE段上的任意点的压缩系数为正, 是热力学系统可能存在的态. 实际上, 这两段对应的物态是亚稳态, 它们比相应的AB'线段和D'E线段上相应的态的自由能要更高

由定义, 在等温状态下

F_{m, f} = F_{m, E} - \int_{E f} p d V_{m}, F_{m, s} = F_{m, E} - \int_{E s} p d V_{m}

于是

F_{m, f} - F_{m, s} = \int_{f E s} p d V_{m} = \oint_{f E s f} p d V_{m} > 0

从而在有限的扰动下, AB,DE上的态可以越过势垒, 过渡到AB',D'E上对应的稳态, 其中AB线段上的状态对应过热液体, DE线段上的状态对应于过冷蒸汽, 或者过饱和蒸汽

Lin's Notes Garden

Explorer

Thermodynamics Final

热力学第一定律

准静态过程的定义和物理意义

功、热、内能的定义及它们之间的关系

热力学第一定律的含义

循环过程效率的定义及其计算

实际气体焦耳-汤姆孙效应的物理来源

Joule-Thomson 实验

绝热节流过程中的不变量

J-T 系数

热力学第二定律和第三定律

可逆过程和不可逆过程的定义和物理意义

热力学第二定律的语言表述、物理含义及其数学表述

Kelvin表述

Clausius表述

两种表述的等价性

在物理中的实际应用

绝热膨胀是不可逆的

绝热线不能相交

气体扩散是不可逆的

熵的宏观定义

Clausius不等式

热温比的积分

熵变计算

熵增加原理

Carnot定理和热力学第二定律的关系

热力学温标的建立

热力学第三定律

Nernst 定理

绝对零度不能达到定理

液体

液体的微观结构

有序性

理论描述

液体分子的热运动

热运动模式

热运动特点

定居时间

外力作用下的行为

表面张力系数的物理含义

表面张力系数

表面功

影响表面张力系数的因素

表面张力的微观解释

拉普拉斯公式

毛细现象

物理解释

液柱高度的计算

相变

相和相变的定义

物态

相

凝聚态

非凝聚态

相变

复相平衡的概念和内容

开放系统的化学势和热力学方程

化学势

相平衡条件

一级、二级相变的基本特征和描述方程

相变分类

相和相变的另一种理解

一级相变

体积跃变和相变功

相变潜热

Clapeyron方程

相变举例

麦克斯韦等面积法则的物理意义

气液等温相变

Van der Waals等温线

极值轨道

Van der Waals方程的不足

正压区的方程

气液共存时两相的物质的量之间的关系

过冷蒸汽和过热液体

Graph View

Table of Contents

Backlinks