一致收敛性

函数列

函数列 $f_{1}, f_{2}, \dots, f_{n}, \dots$ 代入 $x = x_{0}$ 可以得到数列 $f_{1} (x_{0}), f_{2} (x_{0}), \dots$ 若此数列收敛, 则称函数列在点 $x_{0}$ 收敛, $x_{0}$ 为该函数列的收敛点, 反之则称函数列在点 $x_{0}$ 发散. 函数列在数集 $D$ 上的每一个点都收敛, 则称函数列在数集 $D$ 上收敛, 此时可定义函数列的极限函数

f (x) = x \to \infty lim f_{n} (x), x \in D

使得函数列 ${f_{n}}$ 收敛的全体收敛点的几何, 被称为函数列的收敛域

若对 $\forall ε > 0$ 总存在正整数 $N$ 使得当 $n > N$ 时, 对一切 $x \in D$ , 都有

∣ f_{n} (x) - f (x) ∣ < ε

则称函数列 ${f_{n}}$ 在 $D$ 上一致收敛于 $f$ , 记作

f_{n} (x) ⇉ f (x) (n \to \infty)

和函数的一致收敛相似, 这里的 $N$ 仅仅是 $ε$ 的函数, 而与 $x$ 的取值无关 这个命题的否定是: 存在 $ε_{0} > 0$ , 对任何正整数 $N$ , 都有 $D$ 上的某一点 $x^{'}$ 和正整数 $n^{'} > N$ 使得

∣ f_{n^{'}} (x^{'}) - f (x^{'}) ∣ \geq ε_{0}

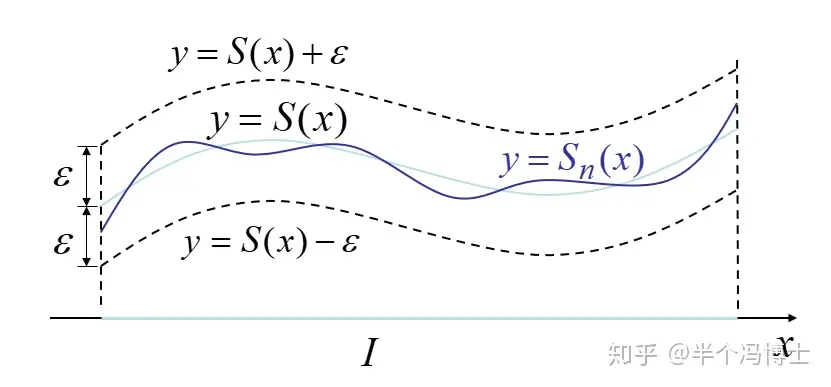
函数列一致收敛的几何意义是: 对任何 $ε > 0$ , 对于一切序号大于 $N$ 的曲线 $y = f_{n} (x)$ 都落在以曲线 $y = f (x) + ε$ 和 $y = f (x) - ε$ 为边的带形区域内

函数列一致收敛的Cauchy准则

函数列 ${f_{n}}$ 在数集 $D$ 上一致收敛的充要条件是: 对 $\forall ε > 0$ , 总存在正数 $N$ , 使得当 $n, m > N$ 时, 对一切 $x \in D$ 都有

∣ f_{n} (x) - f_{m} (x) ∣ < ε

如果已经知道函数列的极限函数, 利用如下定理来判别一致收敛性更为方便: 函数列 ${f_{n}}$ 在区间 $D$ 上一致收敛于 $f$ 的充要条件是

n \to \infty lim x \in D sup ∣ f_{n} (x) - f (x) ∣ = 0

由此得到推论: 函数列 ${f_{n}}$ 在 $D$ 上不一致收敛于 $f$ 的充分必要条件是: 存在 ${x_{n}} \in D$ 使得 $∣ f_{n} (x_{n}) - f (x_{n}) ∣$ 不收敛于 $0$

内闭一致收敛

设函数列 ${f_{n}}$ 和 $f$ 定义在区间 $I$ 上, 若对任意闭区间 $[a, b] \subset I$ , ${f_{n}}$ 在 $[a, b]$ 上一致收敛于 $f$ , 则称 ${f_{n}}$ 在 $I$ 上内闭一致收敛于 $f$ 若 $I = [α, β]$ 是有界闭区间, 则 ${f_{n}}$ 在 $I$ 上内闭一致收敛于 $f$ 和 ${f_{n}}$ 在 $I$ 上一致收敛于 $f$ 是等价的内闭一致收敛是比函数一致收敛更弱的条件, 例子

$f_{n} (x) = x^{n}$ 在 $[0, 1)$ 上不一致收敛于 $f$ , 但对 $\forall δ > 0$ , $x \in [0, δ] sup ∣ x^{n} ∣ \leq δ^{n} \to 0 (n \to \infty)$ , 故其在 $[0, 1)$ 上内闭一致收敛

函数项级数

设 ${u_{n} (x)}$ 是定义在数集 $E$ 上的一个函数列, 表达式

u_{1} (x) + u_{2} (x) + \dots + u_{n} (x) + \dots, x \in E

称为定义在 $E$ 上的函数项级数, 简记为 $\sum u_{n} (x)$ . 并定义部分和函数列

S_{n} (x) = k = 1 \sum n u_{k} (x)

若部分和函数列在点 $x$ 收敛, 则称该函数项级数在点 $x$ 收敛. 在区间上收敛的定义类似

若部分和函数列在数集 $D$ 上一致收敛于 $S (x)$ , 则称该级数在 $D$ 上一致收敛于 $S (x)$

函数项级数一致收敛的Cauchy准则

$\forall ε > 0, \exists N \in N^{*}, s.t. n > N ⟹$

\forall x \in D, p \in N^{*} ∣ S_{n + p} (x) - S_{n} (x) ∣ < ε

并定义余项

R_{n} (x) = S (x) - S_{n} (x)

有推论, 另一个充要条件

n \to \infty lim x \in D sup ∣ R_{n} (x) ∣ = 0

比较函数列的收敛条件就是把 $f$ 换成了 $S = \sum f$

函数项级数一致收敛的其他判别法

Werierstrass 判别法

充分条件: 对于定义在 $D$ 上的函数项级数 $\sum u_{n} (x)$ , 如果 $\sum M_{n}$ 是收敛的正项级数, 若对一切 $x \in D$ 有

∣ u_{n} (x) ∣ \leq M_{n}, n = 1, 2, \dots

则称函数项级数 $\sum u_{n} (x)$ 在 $D$ 上一致收敛

由此知函数项级数

\sum \frac{sin n x}{n ^{2}}, \sum \frac{cos n x}{n ^{2}}

在 $R$ 上一致收敛

Werierstrass 判别法也称为M判别法或者优先级数判别法. 若满足上述条件, 则称级数 $\sum M_{n}$ 在 $D$ 上优先于级数 $\sum u_{n} (x)$ , 或称前者为后者的优级数

Abel 判别法

充分条件:

$\sum u_{n} (x)$ 在区间 $I$ 上一致收敛
对于每一个 $x \in I$ , ${v_{n} (x)}$ 是单调的
${v_{n} (x)}$ 在 $I$ 上一致有界, 即存在正数 $M$ , 使得 $\forall x \in I, n \in N^{*}$ 有 $∣ v_{n} (x) ∣ < M$

Dirichlet 判别法

充分条件

$\sum u_{n} (x)$ 的部分和函数列在 $I$ 上一致有界
对于每一个 $x \in I$ , ${v_{n} (x)}$ 是单调的
在 $I$ 上 $v_{n} (x) ⇉ 0 (n \to \infty)$

具体讨论: 什么是一致收敛

单点收敛

n \to \infty lim S_{n} (x_{0}) = S (x_{0})

本质上就是普通的数项级数收敛

逐点收敛

对 $\forall x \in D$

n \to \infty lim S_{n} (x) = S (x)

一致收敛

对 $\forall ε > 0, \exists N (ε) \in N^{*} s.t. \forall x \in I, n > N ⟹$

∣ R_{n} (x) ∣ = ∣ S_{n} (x) - S (x) ∣ < ε

这等价于

n \to \infty lim x \in I sup ∣ R_{n} (x) ∣ = 0

例子:

逐点收敛 - $S_{n} (1), S_{n} (2), S_{n} (3)$ 通过不同的趋势、速度趋向 $S (1), S (2), S (3)$
一致收敛 - $S_{n} (1), S_{n} (2), S_{n} (3)$ 通过相同的趋势、速度趋向 $S (1), S (2), S (3)$

一致收敛函数列和函数项级数的性质

极限可交换性

${f_{n} (x)}$ 一致收敛时

x \to x_{0} lim n \to \infty lim f_{n} (x) = n \to \infty lim x \to x_{0} lim f_{n} (x)

连续性推论

若函数列 ${f_{n}}$ 在区间 $I$ 上一致收敛, 且每一项都连续, 则其极限函数 $f$ 也在 $I$ 上连续

因为由极限可交换性, $\forall x_{0} \in I, x \to x_{0} lim f (x) = n \to \infty lim f_{n} (x_{0}) = f (x_{0})$ , 故得 $f$ 的连续性

由于 $f (x)$ 在 $x$ 上的连续性只和 $x$ 附近的性质有关, 故上述推论的条件可弱化为内闭一致收敛

可积性

若函数列 ${f_{n}}$ 在 $[a, b]$ 上一致收敛, 且每一项都连续, 则

\int_{a}^{b} n \to \infty lim f_{n} (x) d x = n \to \infty lim \int_{a}^{b} f_{n} (x) d x

也就是说一致收敛情况下, 积分和求极限的顺序可以互换

可微性

\frac{d}{d x} (n \to \infty lim f_{n} (x)) = n \to \infty lim \frac{d}{d x} f_{n} (x)

可微性推论

设 $x_{0} \in I$ 为 ${f_{n}}$ 的收敛点, 且 ${f_{n}^{'}}$ 在 $I$ 上内闭一致收敛, 则 $f$ 在 $I$ 上可导, 且

f^{'} (x) = n \to \infty lim f_{n}^{'} (x)

连续性

若函数项级数 $\sum u_{n} (x)$ 在区间 $[a, b]$ 上一致收敛, 且每一项都连续, 则其和函数在 $[a, b]$ 上连续

也就是说, 在一致收敛的情况下, 无限项求和和求极限可以互换

\sum (x \to x_{0} lim u_{n} (x)) = x \to x_{0} lim (\sum u_{n} (x))

逐项求积

\sum \int_{a}^{b} u_{n} (x) d x = \int_{a}^{b} \sum u_{n} (x) d x

逐项求导

\sum (\frac{d}{d x} u_{n} (x)) = \frac{d}{d x} (\sum u_{n} (x))

Lin's Notes Garden

Explorer

Function Series