波的叠加和干涉
波的叠加原理
波的独立传播定律: 当两列(或多列)波同时存在时, 在它们的交迭区域内, 每个点的振动是各列波单独在该点产生振动的线性迭加, 表述为:
U(p,t)=U1(p,t)+U2(p,t)+⋯
注意这里独立传播的是振动, 而不是光强或者振幅
光波在真空中总是独立传播的, 而在媒质中, 有时会违反独立传播定律, 出现"非线性"
波的干涉和相干条件
合成波
U~(p,t)=U~1(p,t)+U~2(p,t)
合成波的强度
I(p)=U~(p,t)⋅U~∗(p,t)=I1(p)+I2(p)+2A1(p)⋅A2(p)cos[(ω1−ω2)t+δ(p)]
其中\overline表示平均值, 且有
δ(p)=φ1(p)−φ2(p)
和干涉项
2A1(p)⋅A2(p)cos[(ω1−ω2)t+δ(p)]
要让上面这项不为0, 我们有相干条件
- 频率相同
- 存在着相互平行的振动分量
- 存在着稳定的相位差
普通光源发光的机制
原子和分子(微观客体)内部的能量改变特点:
- 不同原子或分子所发射的波列在振动方向和位相上相互独立, 没有联系
- 每个原子或分子发光的持续时间极短
所以两个普通光源发出的光波之间很难相干
几个重要的时间间隔:
- 光扰动的时间周期: T∼10−15 sec
- 实验观测的时间(人眼的响应时间): τ∼10−1 sec
- 探测器响应时间: Δt∼10−9 sec
由于τ>>Δt>>T 所以**无论是实际观察还是仪器接收, 得到的都不可能是某一瞬间的扰动分布, 而只能是扰动强度的时间平均值, 即强度. **
相干光源和非相干光源:
- 两光源间有固定的位相差, 因而按振幅进行迭加, 那么它们称为相干光源
- 而若两光源之间没有固定的位相差, 因而按强度进行迭加, 则称为非相干光源
干涉的反衬度
反衬度(可见度):
γ=IM+ImIM−Im,0≤γ≤1
对于两束光的干涉
γ=I1+I2A1⋅A2⋅1−A1⋅A2⋅(−1)=I1+I22A1⋅A2
此时I=(I1+I2)(1+γcosδ)
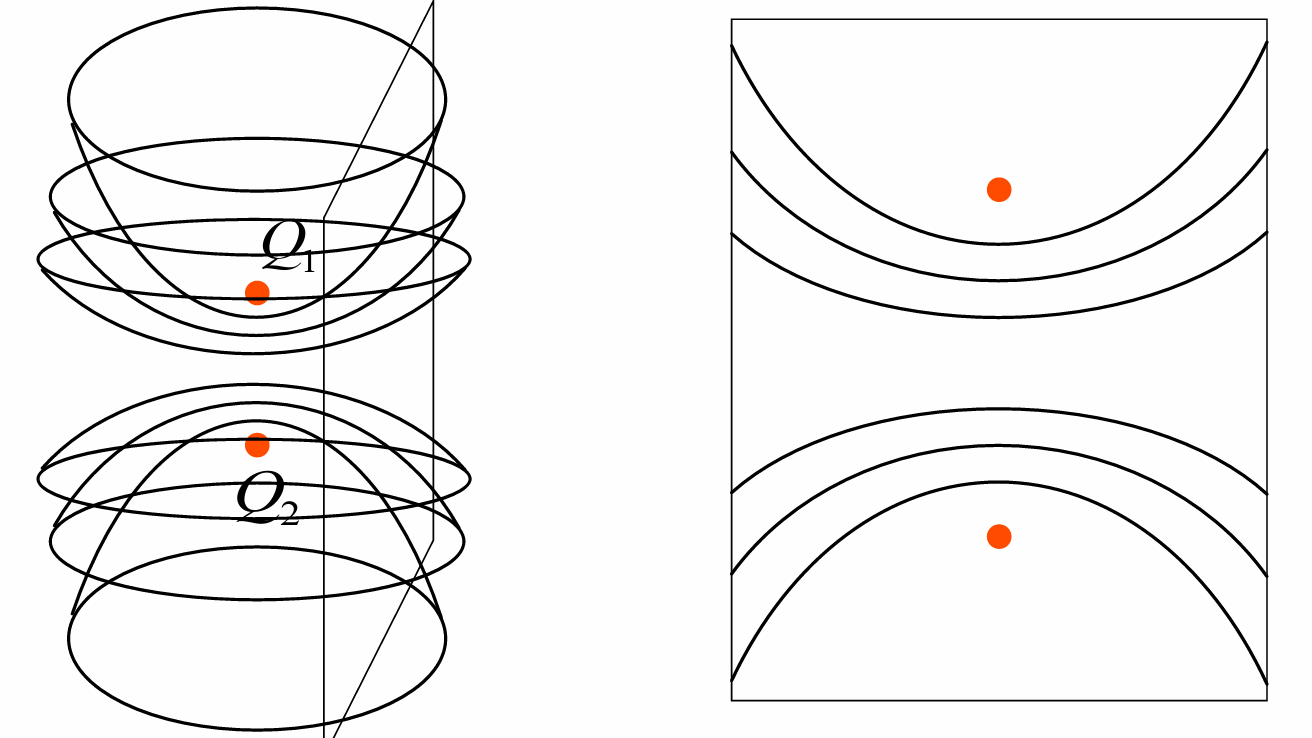
两个点源的干涉
两列球面波的干涉
设有两个强度相等的相干光源Q1,Q2, 在r1,r2≫Q1Q2的情况下有
δ(p)=λ2π(r1−r2)
故条纹
{max,min,r1−r2=kλr1−r2=(k+1/2)λ
等强面为回转双曲面
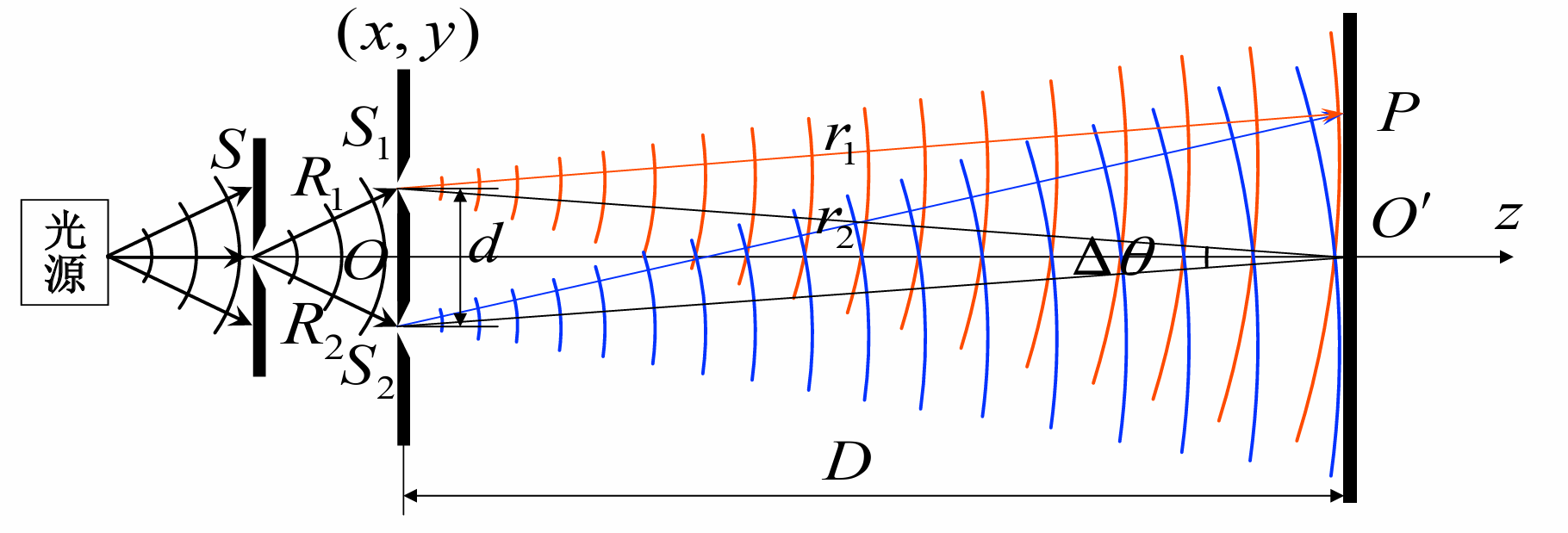
杨氏(T. Young, 1801)双缝实验
 强度分布
强度分布
I(x′,y′)=4(Da)2cos2(λDπdx′)
条纹间距
Δx=dλD
Young氏实验最重要的一点在于: 利用次光源分解, 巧妙地获得了相干光源
两束平行光的干涉
两束平行光束的传播方向为(α1,β1,γ1),(α2,β2,γ2)
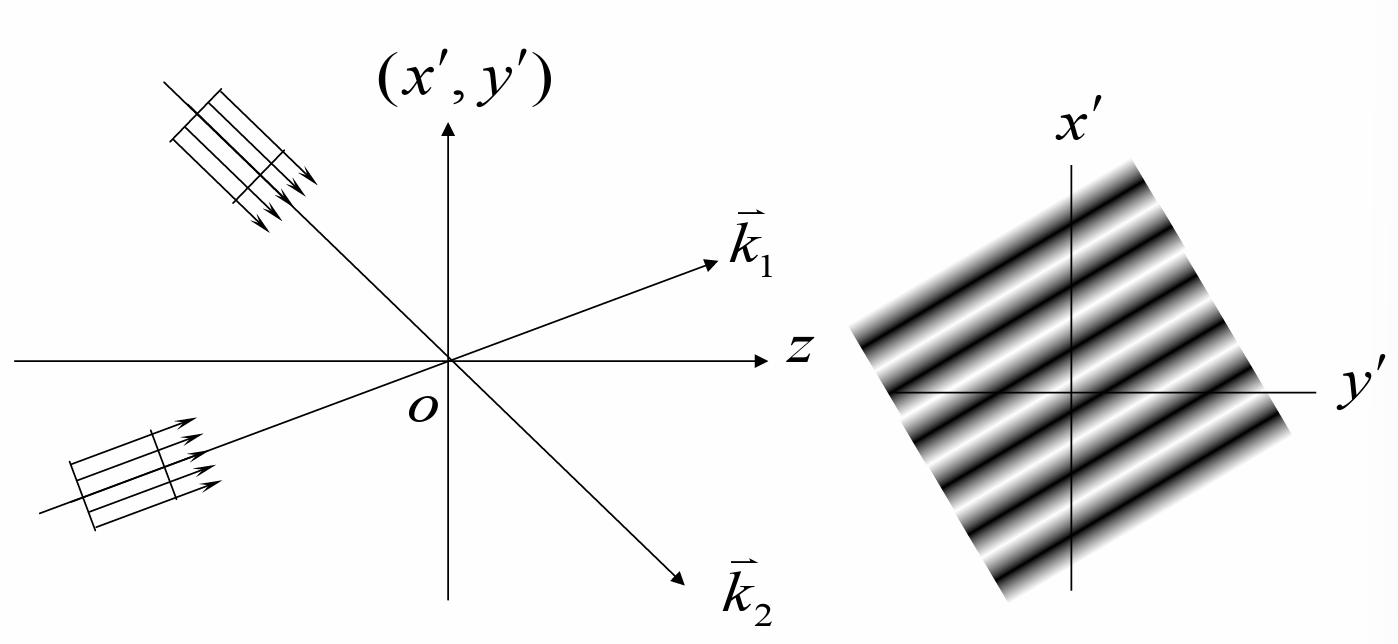 在z=0的波前上
在z=0的波前上
{φ1(x′,y′)φ2(x′,y′)=k(x′cosα1+y′cosβ1)−φ10=k(x′cosα2+y′cosβ2)−φ20δ(x′,y′)=kx′(cosα1−cosα2)+ky′(cosβ1−cosβ2)+φ20−φ10I(x′,y′)=(A12+A22){1+γcos[kx′(cosα1−cosα2)+ky′(cosβ1−cosβ2)+φ20−φ10]}
有反衬度
γ=1+(A1/A2)22A1/A2=A12+A222A1A2
空间频率
凡是有周期, 就可以引入频率
干涉条纹的间隔
⎩⎨⎧Δx′=cosα1−cosα2λΔy′=cosβ1−cosβ2λ
条纹的空间频率
⎩⎨⎧fx′=λcosα1−cosα2fy′=λcosβ1−cosβ2
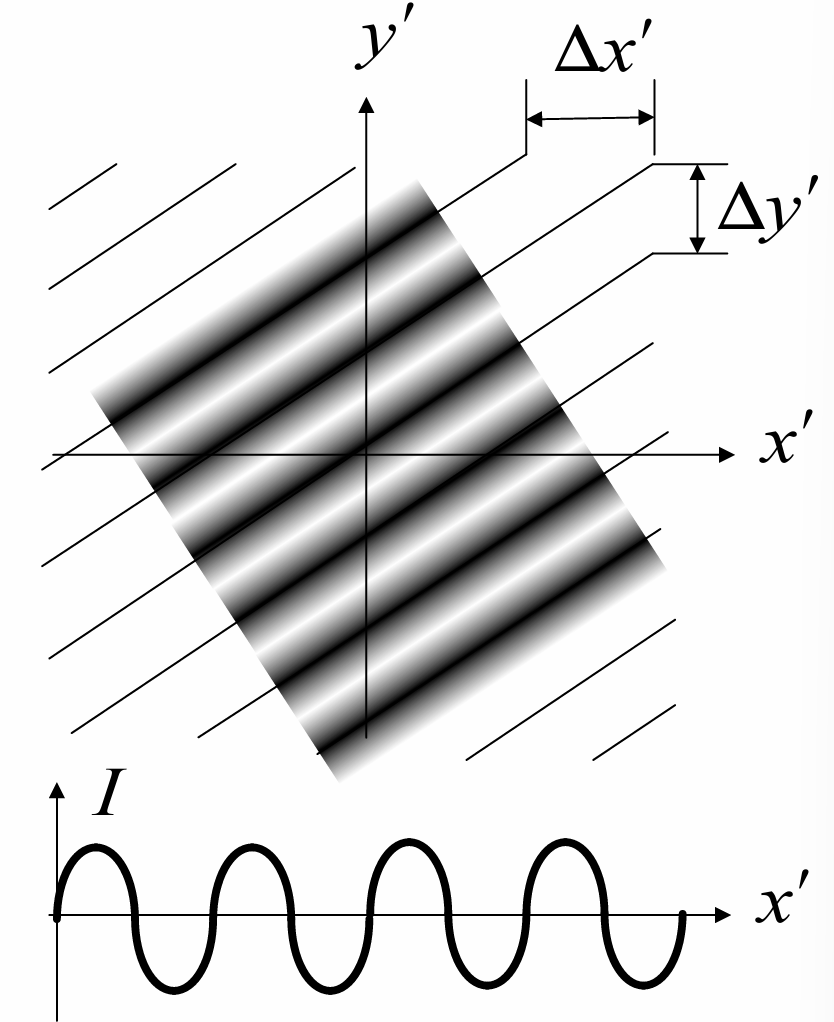

 强度分布
强度分布 在的波前上
在的波前上