Optics Final Review

干涉

振幅的叠加 + 3个相干条件 $\to$ 强度的变化 反衬度

$$\gamma =\frac{I_M-I_m}{I_M+I_m},0\le \gamma \le 1$$

Young氏双缝和它的各种变种(Fresnel 双棱镜, H.Lloyd镜 etc.)

都变换为Young的情况，利用公式

$$\Delta x=\frac{D}{d}\lambda$$

薄膜干涉

光程差

$$\Delta L=2nh\cos i+\frac{\Delta \varphi }{2\pi }\lambda$$

其中$\Delta \varphi =0，\pm \pi$表示潜在的半波损失. 当波从波疏介质($n$小的)垂直入射到波密介质（$n$大的）并从分界面反射回波疏介质时，会产生半波损失. 对于三层两分界面的薄膜模型，“汉堡包”式的情况会产生半波损失

等厚条纹

厚度不均匀薄膜表面的干涉场，取$i\to 0$ 条状干涉条纹

Newton环

利用圆幂定理求出某一半径$r$处空气膜的厚度$h$，可解得

$$r_k=\sqrt{kR\lambda }$$

光学膜

增透膜要求从上到下三层介质的折射率$n_1,n,n_2$满足$n_1<n<n_2$，当$n=\sqrt{n_1{n}_2}$时完全消除反射光

高反膜则要求$n_1<n>n_2$

等倾条纹

厚度均匀薄膜无穷远处的干涉场，取$h=\mathrm{const}$而改变$i$

倾角相等的条纹会形成一个锥，在无穷远的光屏上（即某个凸透镜的焦平面）就是同心圆

因为$2nh\cos i=k\lambda ⟹\cos i_k=\frac{k\lambda }{2nh}\propto k$，所以条纹中心（$i$小）级次高、边缘（$i$大）级次低. $h$增大，条纹从中心生出并向外扩展；$h$减小，条纹向中心会聚并消失于中心

采用拓展光源的好处：光源上各点形成完全一样的干涉图样（强度相加而不是振幅相加），其效果是提高干涉图样的亮度，有益无害. 但是拓展光源对观察等厚条纹会有影响

Michelson 干涉仪

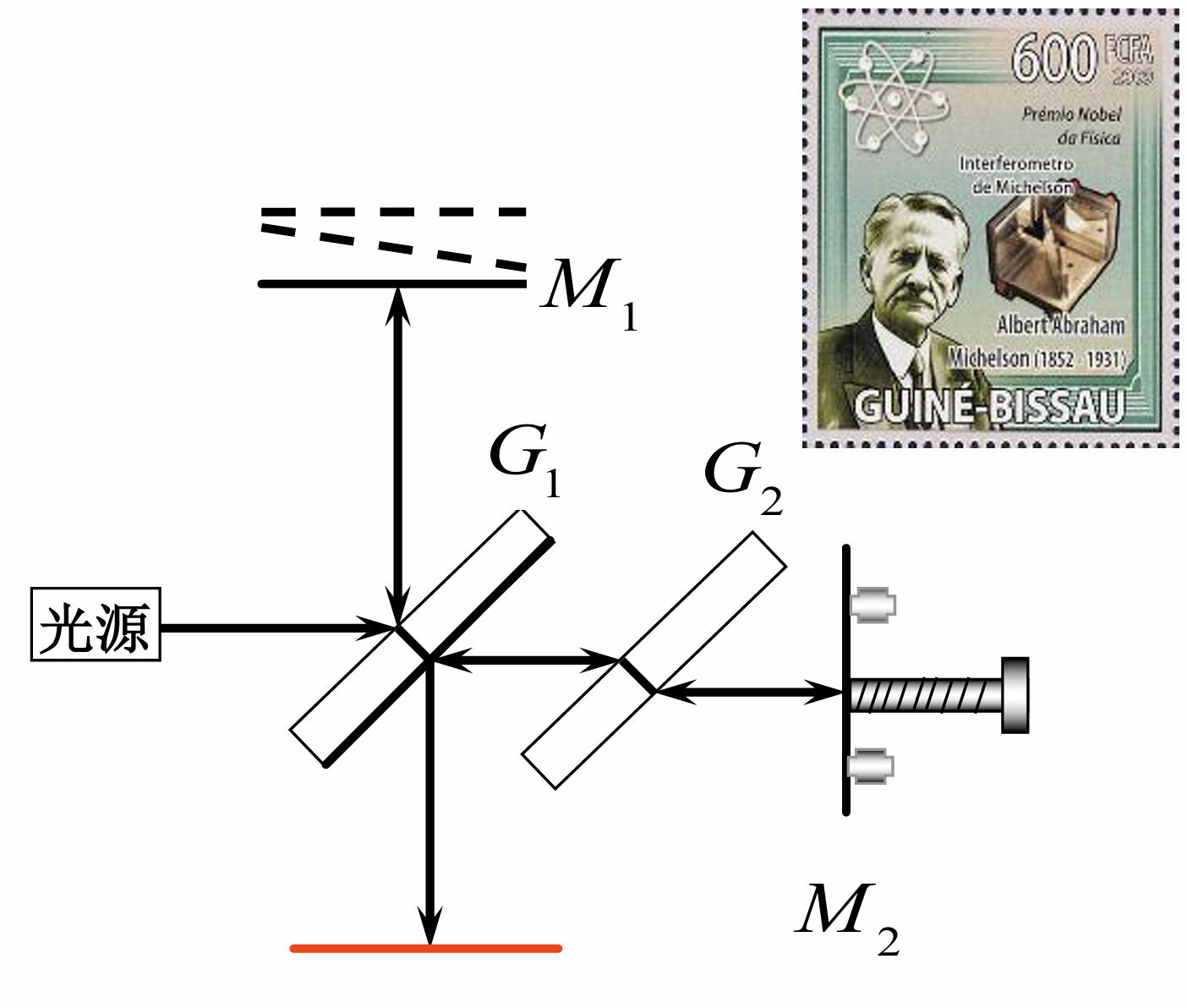
等倾条纹：厚度越大级数越多，条纹越多、越密 其中中心条纹对应$\theta =0$且级数最高，最边缘为$\theta ={\theta }_m$即视场角，级数最低 等厚条纹：厚度越小反衬度越高，厚度大了条纹过密反而看不清

注意

需要注意的是$M1$的移动距离对光程的影响是双倍的，也就是说，$M1$每移动$\frac{\lambda }{2}$距离，视场中心吞或吐一个亮环

光源非单色性对干涉条纹的影响

以双线结构为例子

$$\gamma (\Delta L)=\left|\cos \left(\frac{\Delta k\Delta L}{2}\right)\right|$$

其中$\Delta L$为光程差，$\Delta k$为波数差

条纹的反衬度随光程差作周期振动，振动的角频率为$\frac{\Delta k}{2}$

具体而言$\Delta k=\left(\frac{2\pi }{{\lambda }_1}-\frac{2\pi }{{\lambda }_2}\right)=2\pi \frac{{\lambda }_2-{\lambda }_1}{{\lambda }_1{\lambda }_2}=2\pi \frac{\Delta \lambda }{{\lambda }^2}=\frac{2\pi }{l_0}$ 其中$l_0=\frac{{\lambda }^2}{\Delta \lambda }$为该光线结构光源的相干长度

光场的相干性

产生原因

空间相干性来源于扩展光源不同部分发光的独立性 时间相干性来源于光源发光过程在时间上的断续性

结果

空间相干性主要表现在波场的横向（波前）上，集中体现在分波前干涉装置中； 时间相干性主要表现在波场的纵向（波线）上，集中体现在分振幅干涉装置中

反比公式

空间相干性 $\Delta \theta b\sim \lambda$，即要提升干涉场相对光源的角宽度，就必须减小光源尺度 时间相干性 ${\tau }_0\Delta \nu \sim 1$，即要提升相干的有效时间，就必须改善光源的单色性

相干区域和相干时间都不是一个绝对的界限，实际上相干区域和相干时间内也有非相干的成分，而相干区域和相干时间之外，也有相干的成分，只是主导地位的不同，部分相干是最为普遍的，而反衬度则是相干程度的一种度量

Fabry Perot 干涉仪

多光束干涉可以产生非常细窄的干涉条纹. 这是因为多次反射会增强干涉条纹的清晰度和对比度，薄膜的反射率越高，条纹越尖锐

Fabry Perot干涉仪由两块平行的高反射率玻璃板组成,在两块玻璃板之间形成一个空气间隙， 当光束以一定角度入射到这个系统时,会在玻璃板之间发生多次反射,产生多个相干的光束， 通过调节两块玻璃板之间的间距,可以选择特定波长的光进行传输或反射,从而实现高分辨率的光谱分析

它的光程仍然是

$$\Delta L=2nh\cos i$$

其中$h$是谐振腔宽度，$i$是入射倾角，由此可以推出相位差

$$\delta =\frac{\Delta L}{\lambda }\cdot 2\pi =\frac{4\pi nh\cos i}{\lambda }$$

下面考虑两种情况

光源为单色拓展光源

此时$\lambda$固定，但是有各种可能的倾角$i$，因为只有在特定的方向$i_k$上出现干涉极强，我们关心某一级极大条纹的半角宽$\Delta {\theta }_k$

我们从相位差公式中可以得到

$$\delta =\frac{4\pi nh\cos i}{\lambda }=2k\pi ⟹\cos i_k=\frac{k\lambda }{2nh}$$

两边对$k$求导即有

$$-\sin i_k\cdot \frac{\delta i_k}{\delta k}=\frac{\lambda }{2nh}⟹\Delta i_k=\frac{\lambda }{2nh\sin i_k}$$

实际上由于衬比度的原因，对于实际可见的$\Delta {\theta }_k$需要作出一个修正

$$\Delta {\theta }_k=\frac{\lambda }{2nh\sin {\theta }_k}\cdot F$$

其中修正因子和反射率$R$有关

$$F=\frac{1-R}{\pi \sqrt{R}}$$

光源为非单色平行光

此时$i$固定且接近于$0$，由于多光束干涉，使得在很宽的光谱范围内只有某些特定的波长${\lambda }_k$附近出现极大，这些${\lambda }_k$满足下式

$$2nh=k{\lambda }_k$$

对于${\lambda }_k$附近波长光线的分辨能力，设光波长为$\lambda$的$k$级可分辨的最小波长间隔为$\Delta \lambda$，则有

$$\Delta {\lambda }_k=\Delta \left(\frac{2nh}{k}\right)=-\frac{1}{k}{\lambda }_k$$

于是$\frac{\Delta {\lambda }_k}{{\lambda }_k}$可以修正为

$$\frac{\Delta {\lambda }_k}{{\lambda }_k}=\frac{F}{k}=\frac{1}{\pi k}\frac{1-R}{\sqrt{R}}$$

换成频率，则有$\Delta {\nu }_k\propto \Delta (\frac{1}{\lambda })\propto \Delta \left(\frac{k}{2nh}\right)=\frac{1}{2nh}\propto \frac{{\nu }_k}{k}$，故也有

$$\frac{\Delta {\nu }_k}{{\nu }_k}=\frac{F}{k}=\frac{1}{\pi k}\frac{1-R}{\sqrt{R}}$$

对于波长范围${\lambda }_l\sim {\lambda }_r$的非单色光，出现极大的间隔（又称为纵模频率间隔）为$\Delta \nu =\frac{c}{2nh}$，于是可以出现的谱线（又称为纵模）数目为$(\frac{c}{{\lambda }_l}-\frac{c}{{\lambda }_r})/\Delta \nu$，其中每条谱线分别对应的宽度就是$\Delta {\nu }_k$，换成波长宽就是$\Delta {\lambda }_k$

换言之，公式$2nh=k{\lambda }_k=\frac{ck}{{\nu }_k}$确定了每一个极大条纹出现的位置和总的条纹数目（和$F$无关），而$\Delta {\nu }_k$和$\Delta {\lambda }_k$确定了每一条亮纹对应的衬比度意义上的频率宽度和波长宽度（需要$F$修正）

衍射

衍射的本质可以看作多光束干涉，只是这个“多”趋于无穷大

Huggens-Fresnel原理

空间某点的振动可看作波前上所有面元所发次波在该点的相干叠加 ，数学上表述为

$$\tilde{U}(p)=\underset{(\Sigma )}{\iint }\mathrm{d}\tilde{U}(p)$$

Babinet原理

互补屏衍射场的复振幅之和等于自由传播波场

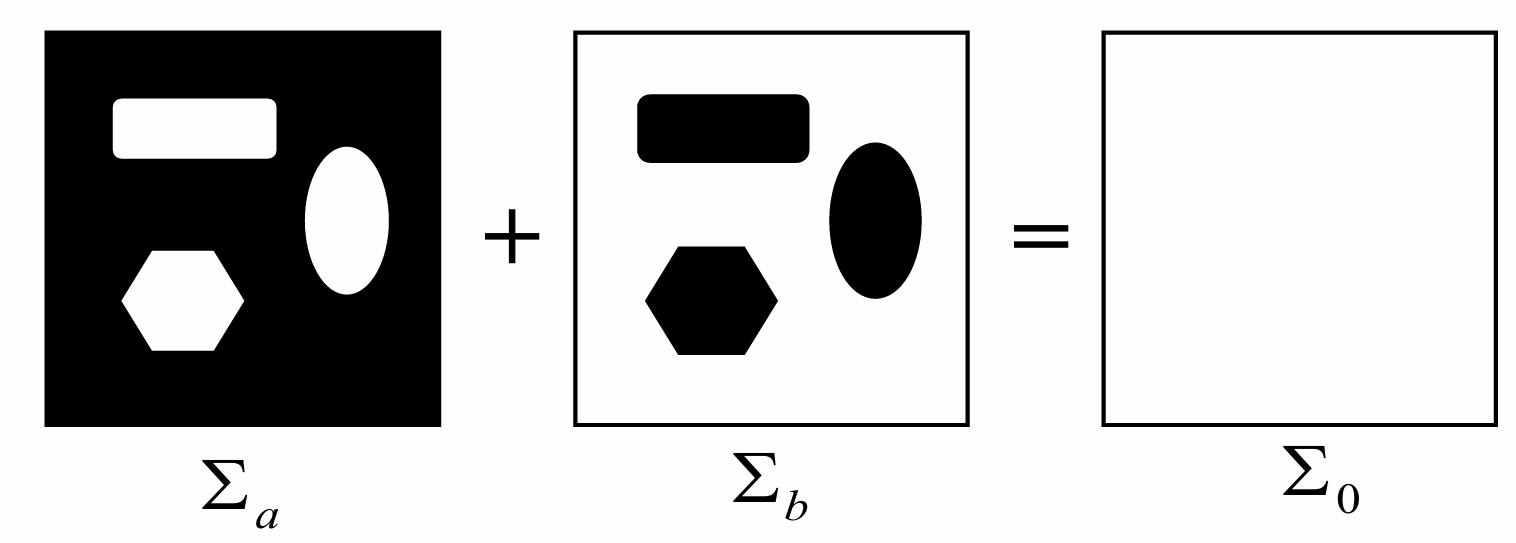
Fresnel衍射

定义：光源或接收屏与衍射屏的距离为有限远

半波带法

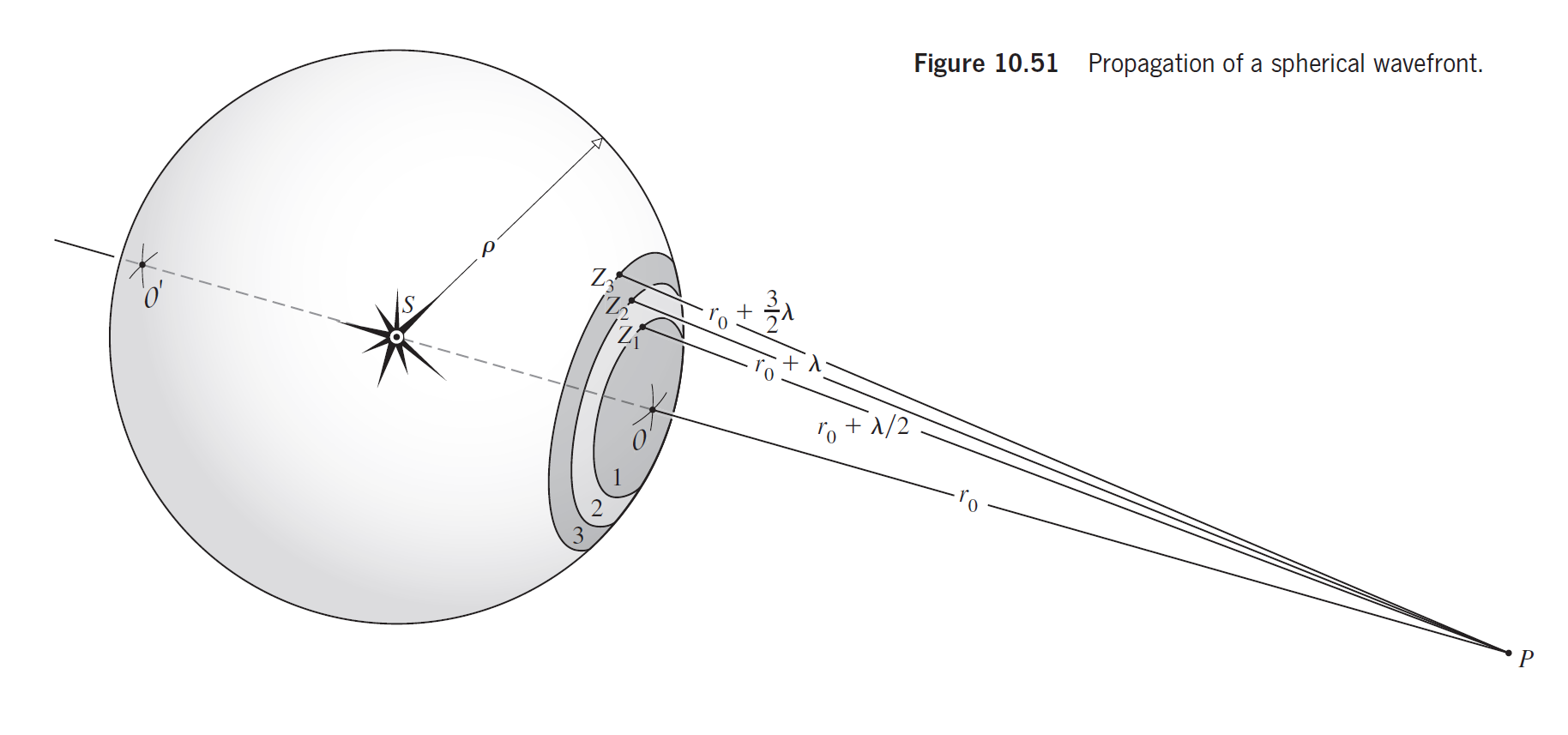把波面分割成一个个的半波带，相邻半波带到像点的距离逐个相差半个波长（名字的来源）

在这种情况下，相邻半波带贡献的复振幅${\tilde{E}}_1,{\tilde{E}}_2,\dots$的相位差为$\pi$，它们可以相互抵消.

在自由传播时，可以通过积分得出整个波前在像点产生的振幅是第一个半波带的效果之半，即

$$E_0=\frac{E_1}{2}$$

矢量图解法

我们再把每个半波带分成$N$个子区域

$$r_0+\frac{\lambda }{2N},r_0+\frac{\lambda }{N},r_0+\frac{3\lambda }{2N},\dots ,r_0+\frac{\lambda }{2}$$

把它们用矢量来表示，合成的振幅是$E_1=2E_0$（$E_0$是自由传播时中心点的振幅），矢量形成的类圆弧称为振动曲线 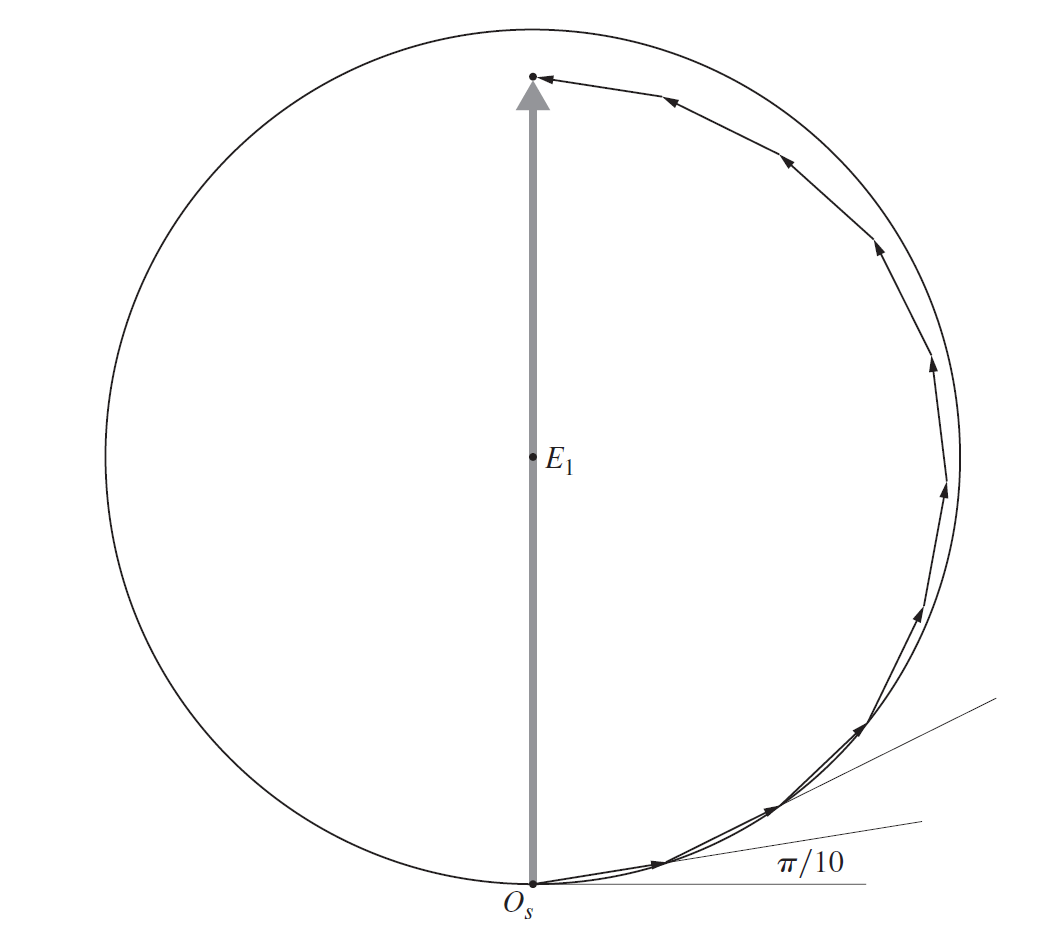对于每一个半波带，振动曲线绕半圈，直到最后终于某一个半波带的某一个位置 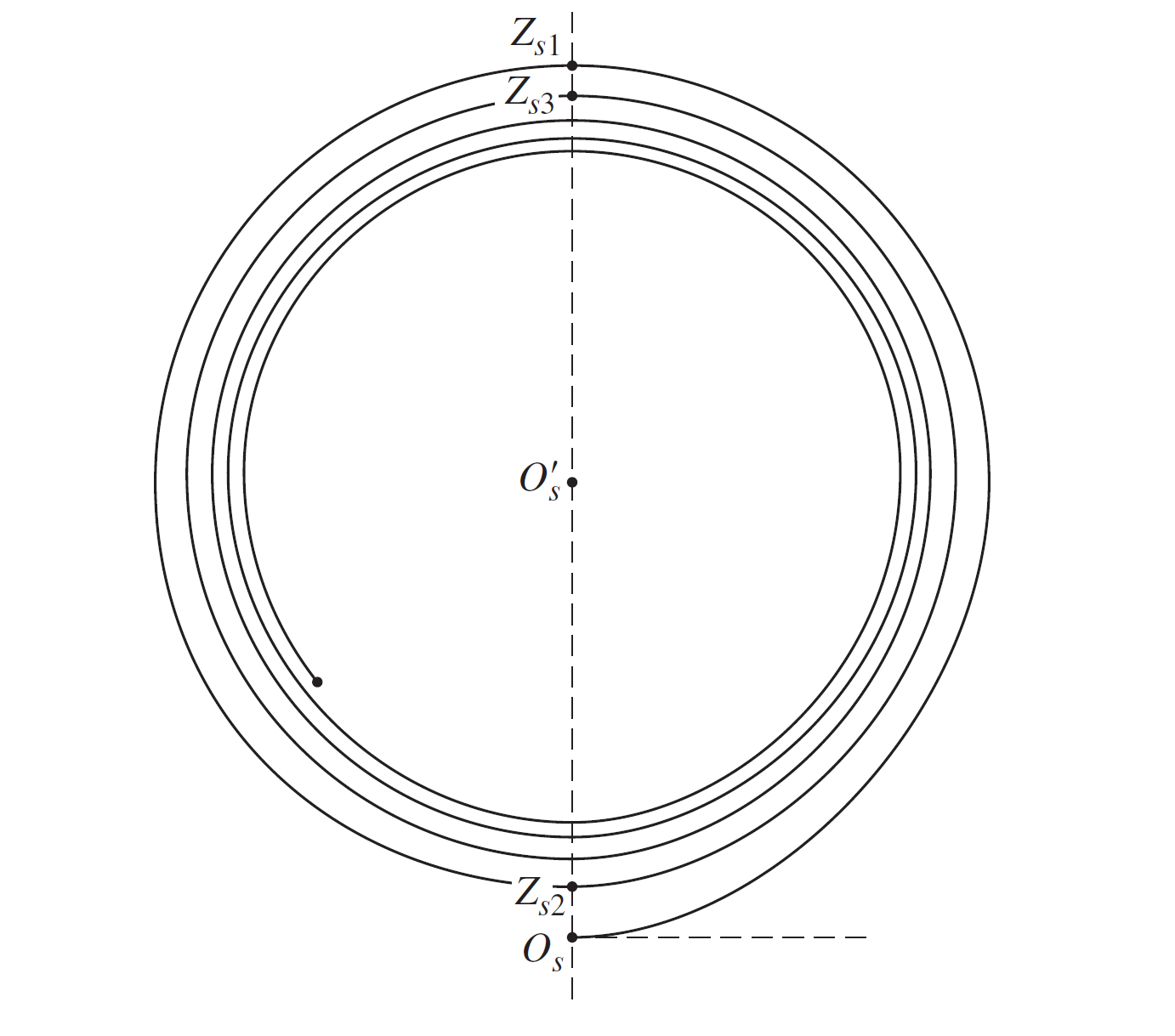对于一个球面波，考虑圆孔衍射，光屏上轴点$P$能接收到的光线是波前的一部分，这个点接受到的振幅和孔（光阑）的大小有关，我们的振动曲线将终止于一个半径为$r$的位置带，这个圆环位置上的点发出的次波恰好不能通过圆孔 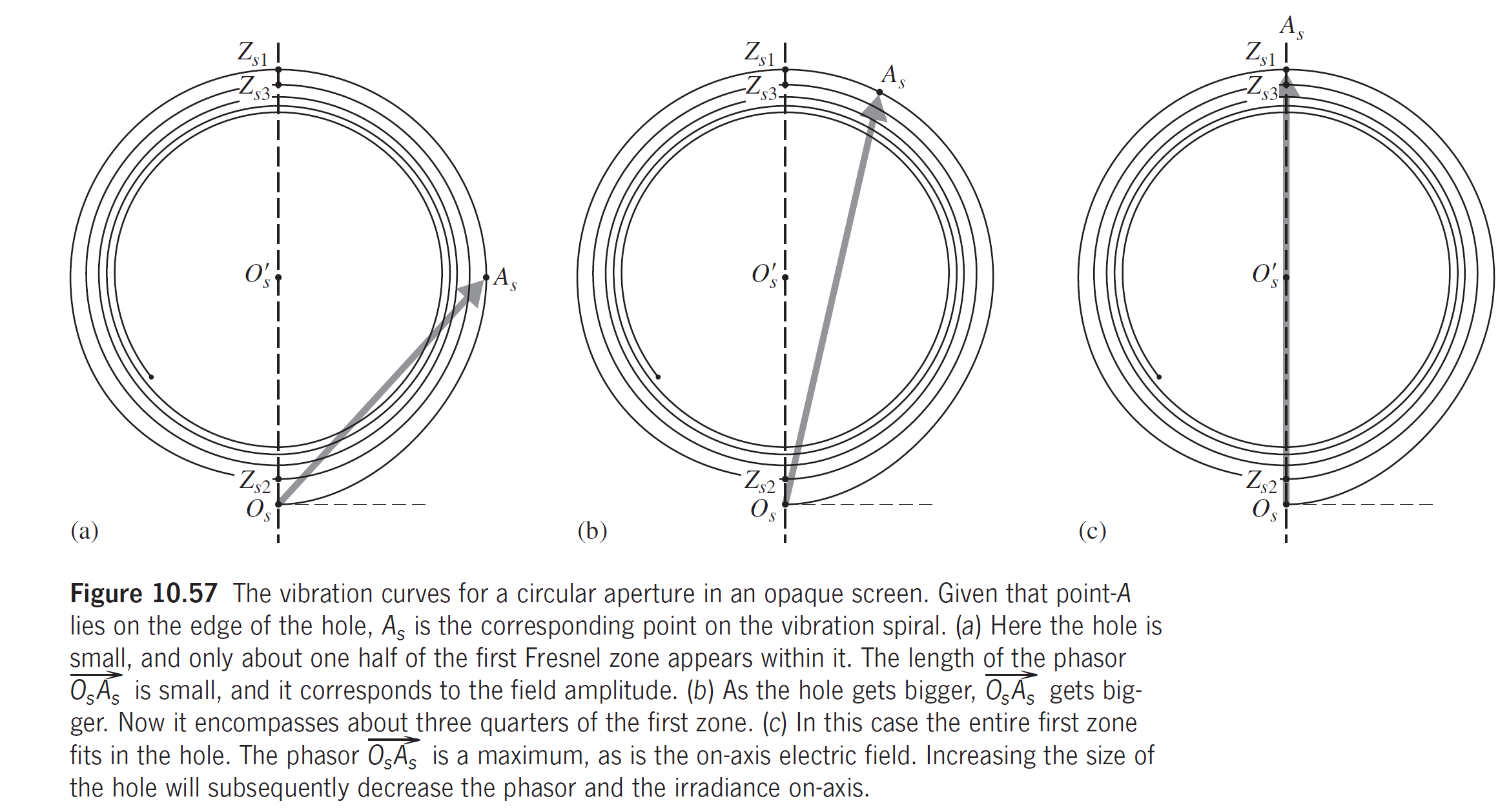当圆孔的大小合适时，合成的振幅能够取到最大值$E_1$，振幅为自由传播时的两倍. 这告诉我们，在屏和光源之间加上阻碍后，轴点$P$的振幅将可能变成原来的两倍，光强变成原来的四倍；由能量守恒可知其他地方的光强必然会降低.

如果我们构造一个光阑，令奇数半波带透光，而偶数半波带都涂黑（Fresnel波带片），就可以极大地增大$P$处的光强

上面是对光屏上中心点的分析，现在考虑每一个点，每一个点能对应的贡献振幅的半波带是不同的 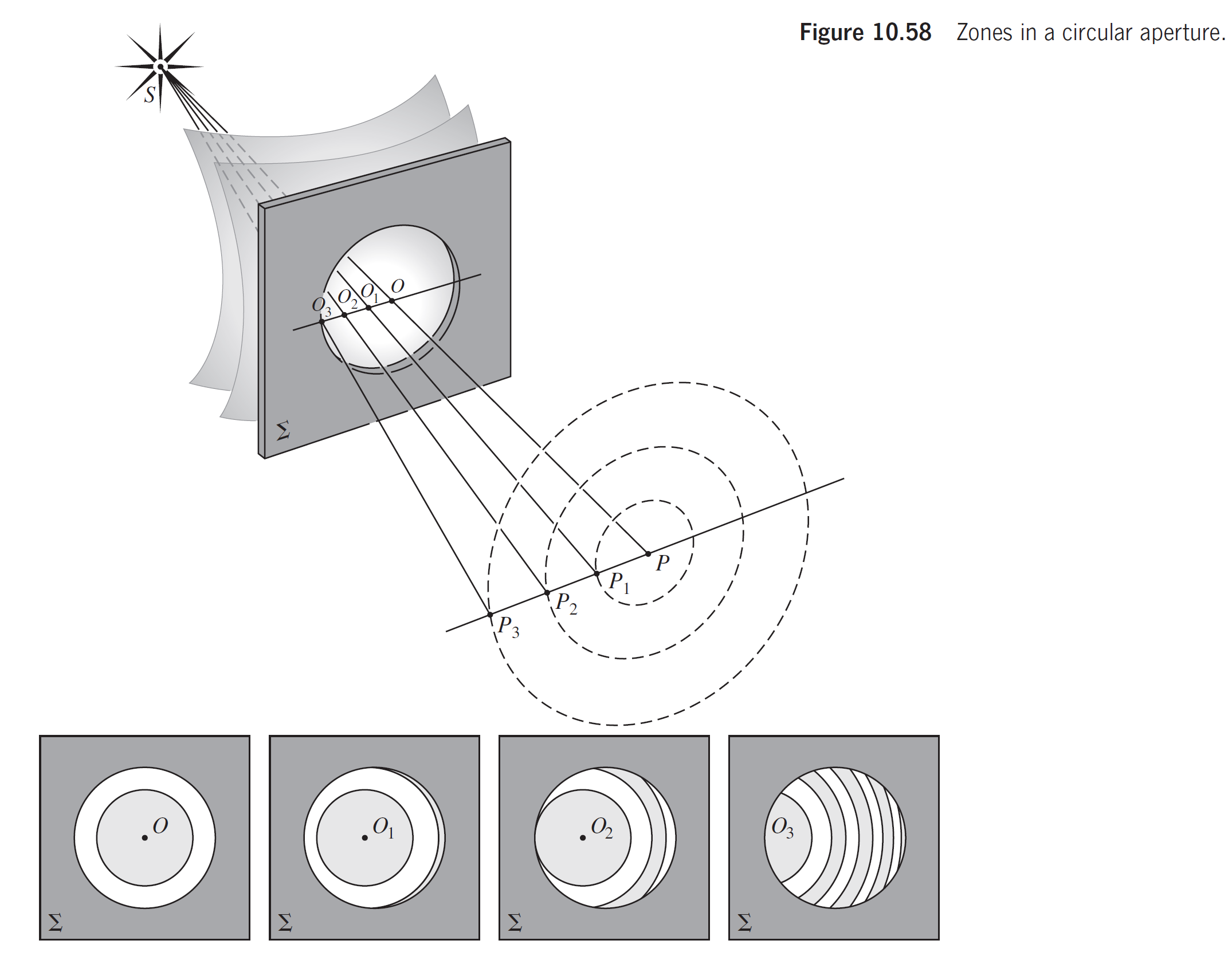孔径的区域内的半波带数量取决于点$P$到点$O$的距离$r_0$. 当点$P$沿着中心轴的任一方向移动时，半波带的数量无论增加还是减少都在奇数和偶数之间振荡. 因此，光强将经历一系列最大值和最小值，形成的衍射条纹

Fresnel 透镜

Fresnel透镜

光源$S$通过Fresnel波带片形成了一个光斑$P$, 如果把$S,P$分别看成物点、像点，则构成了Fresnel透镜，考虑通过第$m$个半波带（半径为${\rho }_m$）的光路的光程和直射光路的光程的差

$$\Delta L=\sqrt{s^2+{\rho }_m^2}+\sqrt{s^{\prime 2}+{\rho }_m^2}-s-s^{\prime }=\frac{{\rho }_m^2}{2s}+\frac{{\rho }_m^2}{2s^{\prime }}$$

故其物象关系为

$$\Delta L=m\lambda ⟹\frac{1}{s}+\frac{1}{s^{\prime }}=\frac{m\lambda }{{\rho }_m^2}=\frac{\lambda }{{\rho }_1^2}$$

此我们可以给出Fresnel透镜的焦距（即该波带片的焦距）为

$$f=\frac{{\rho }_1^2}{\lambda }$$

直边衍射

用直刀口将点光源的波前遮住一半，相当于每一个半波带都损失一半，但是相对的相位关系仍然不变，对应的像点的振幅变成原来的一半，亮度变成自由传播时的四分之一（因为没有有圆孔完全遮挡一部分半波带所以直边衍射不能带来中心振幅的增益）

Fraunhofer衍射

形成衍射场的条件

接收屏幕应该放得足够远，由电磁波的远场条件知道接收屏和衍射屏之间的距离$z$需要满足

$$z\gg \frac{a^2}{\lambda }$$

其中$a$为衍射屏的线度，可取为孔径大小

接收屏幕上能形成Fraunhofer衍射图样的几何限度$\rho$也需要满足电磁波的傍轴条件，也就是

$$\rho \ll z$$

单缝的矢量图解法

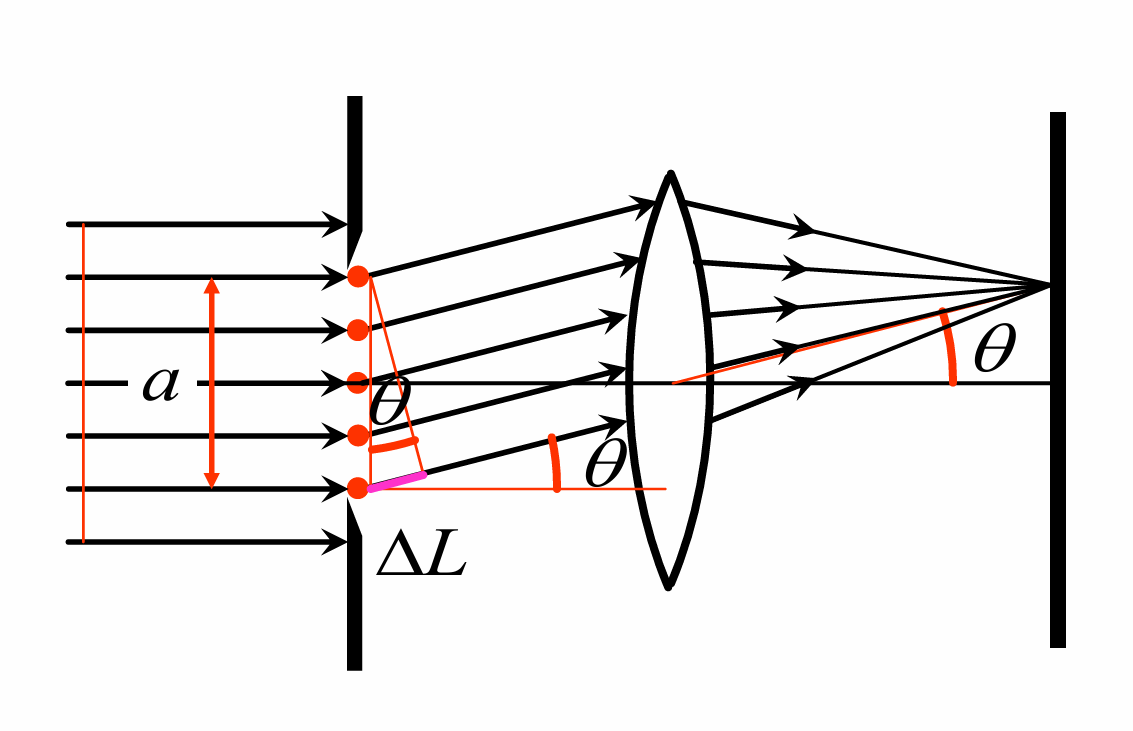用矢量图解法来分析屏上一点$P(\theta )$的振幅，该点对应的光程差为

$$\Delta L=a\sin \theta$$

对应的相位差为

$$\Delta \varphi =\frac{\Delta L}{\lambda }\cdot 2\pi =\frac{2\pi a}{\lambda }\sin \theta$$

下图中的(b)和(c)(d)展现了$\Delta \varphi =0$和$\Delta \varphi =\pi$的情况，前者振幅矢量均同向，合成的振幅最大；后者振幅矢量会形成一个半圆，合成的振幅大小为这个半圆的直径

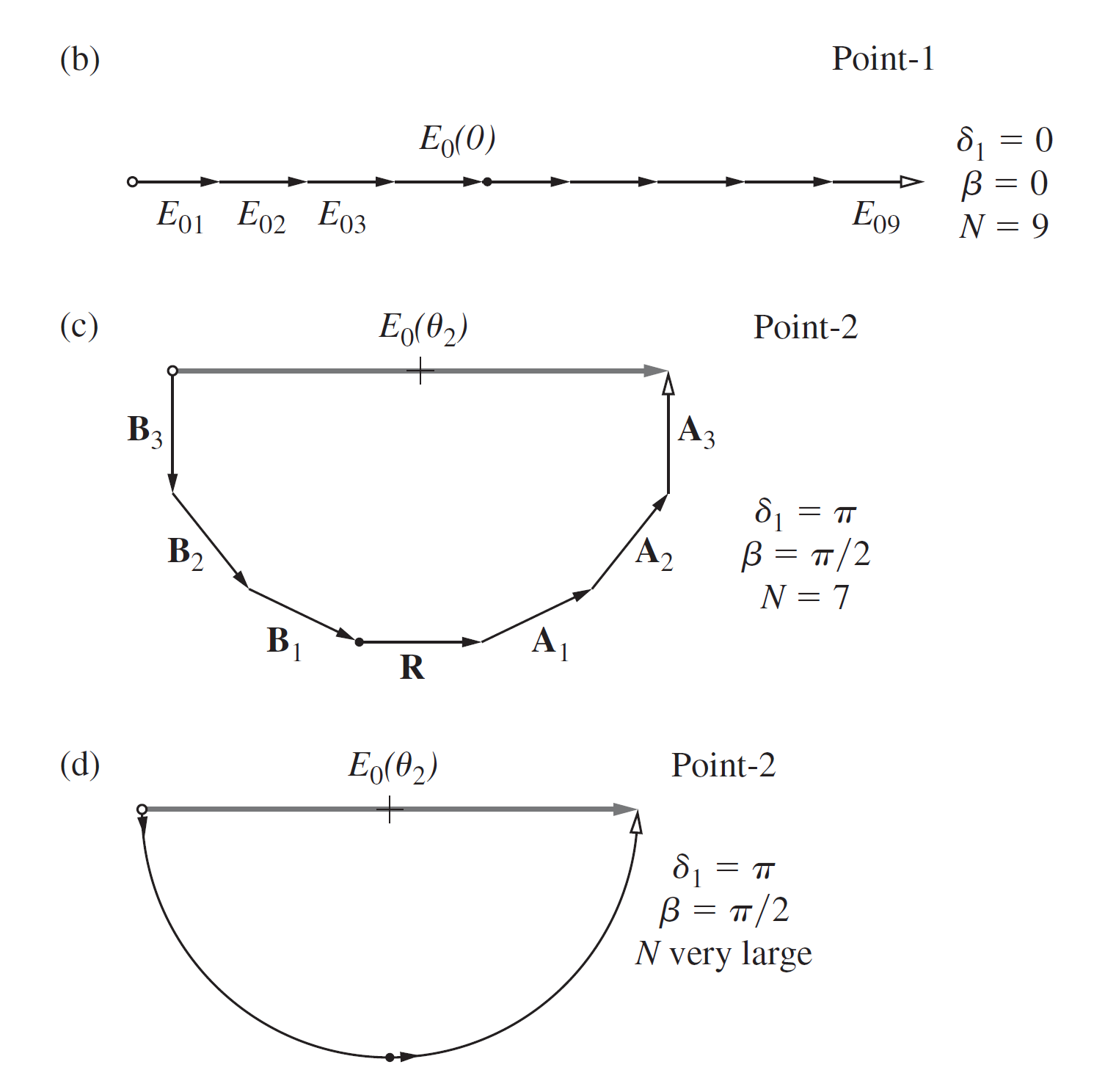再考虑$\Delta \varphi =2k\pi$的点，它们的振幅矢量合成为一个完整的圆，对应的振幅大小为零，相应的$P$点为暗点. 这和两束光干涉的情况完全相反，原因在于双缝干涉是离散的两束光波的合成，而在衍射的情况下有无数连续的光束参与了合成

需要注意的是，当$k$不断增大的时候，振幅曲线的半径因为光的衰减会越来越多，故对$\Delta \varphi =(2k+1)\pi ,k\ge 1$也就是$\Delta L=(k+\frac{1}{2})$的点来说，虽然都是亮点，但随着$k$的增大，亮度会越来越低

上面排除了 $k=0$的情况，这是因为

由于$\Delta L=0$的时候是最亮的点，而$\Delta L=\lambda$的时候是第一个暗点，所以当$\Delta L=\frac{\lambda }{2}$的时候其亮度处于二者之间，不能算作亮点；但是对于$k\ge 1$的情况来说，由于其两侧光程差为$\lambda$整数倍的点都是暗点，故视其为亮点

单缝衍射的定量分析

光斑位置

考虑$k$级暗纹

$$\Delta L=a\sin {\theta }_k=k\lambda ⟹\sin {\theta }_k=k\frac{\lambda }{a}$$

设$x$为定义在屏上的坐标，则

$$x_k=f\tan {\theta }_k$$

其中$k=1,2,3,\dots$ 如果${\theta }_k\to 0$，则有

$$|x_k|\approx fk\frac{\lambda }{a}=k\frac{\lambda }{a}f$$

对于$k$级亮纹，类似地有

$$\sin {\theta }_k=\left(k+\frac{1}{2}\right)\frac{\lambda }{a}$$

其中$k=1,2,3,\dots$ 如果${\theta }_k\to 0$，则有

$$|x_k|=\left(k+\frac{1}{2}\right)\frac{\lambda }{a}f$$

特别地，$0$级亮条纹在$x=0$的位置

光斑宽度

定义$k$级亮纹的角宽度为$\Delta {\theta }_k=\frac{\lambda }{a}$, 其中$k\ne 0$. 当$k=0$时，定义$\Delta {\theta }_0={\theta }_{+1}-{\theta }_{-1}=2\frac{\lambda }{a}$

光斑的几何宽度$\Delta x_k=f\Delta {\theta }_k$，几何直径$D_k=2f\Delta {\theta }_k$

单缝衍射因子

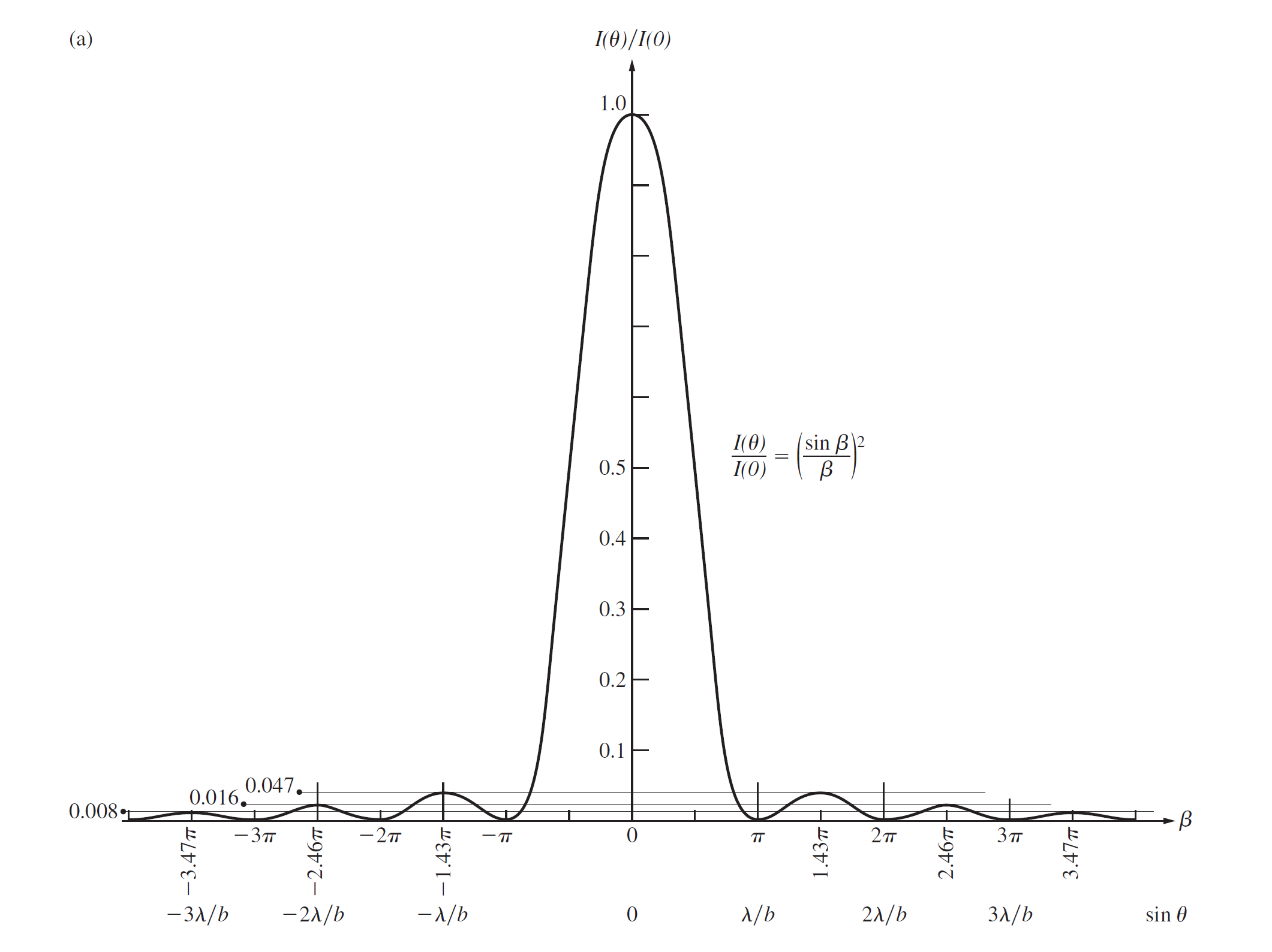
定义$\beta =\frac{\pi a}{\lambda }\sin \theta$（即$\theta$处相位差的一半）, 通过解Fresnel积分可以得到光强$I$关于$\beta$的分布

$$\frac{I(\theta )}{I(0)}={\left(\frac{\sin \beta }{\beta }\right)}^2$$

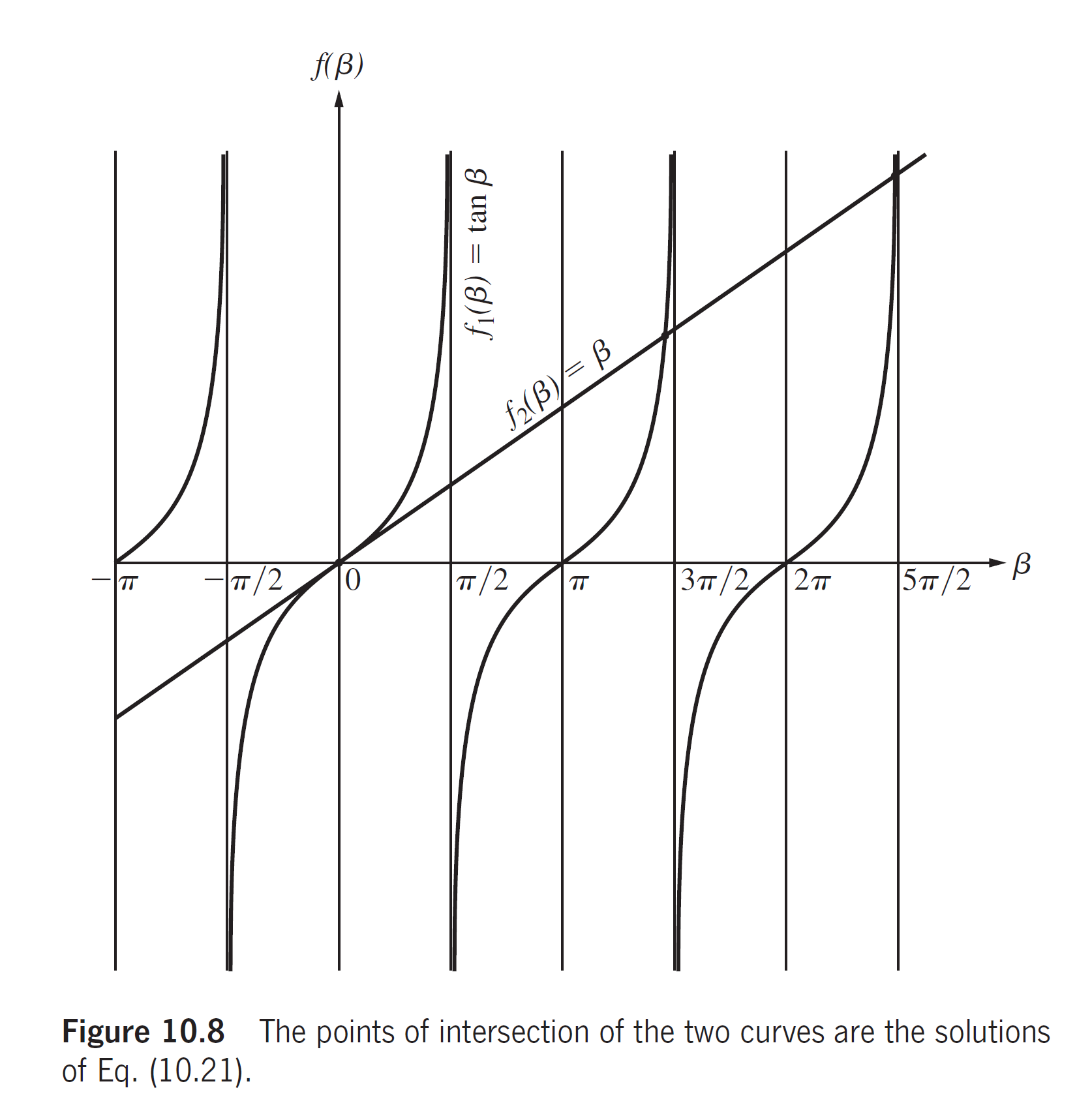解得$I(\theta )$的极大值满足$\beta =\tan \beta$ 可以近似为极大值出现在$\beta =\pm \left(k+\frac{1}{2}\right)\pi$处，作$I\sim \beta$图像

矩孔衍射的情况

光程差

$$\Delta L=-(x\sin {\theta }_1+y\sin {\theta }_2)$$

有

$$I({\theta }_1,{\theta }_2)=I_0{\left(\frac{\sin \alpha }{\alpha }\right)}^2{\left(\frac{\sin \beta }{\beta }\right)}^2$$

衍射反比关系

将角宽度公式$\Delta {\theta }_k=\Delta \theta =\frac{\lambda }{a}$变形，有

$$\Delta \theta \cdot a=\lambda$$

这个反比和空间相干性的反比公式相似，有如下意义

• 当$a$足够大时，$\Delta \theta$足够小，对应于几何光学极限
• 参与干涉的波源数目越多，出现干涉极大的条件越苛刻，能量也越集中在某个特定的方向上
• 说明衍射具有放大作用，可以用于测量单缝或细丝的宽度或直径

斜入射的情况

当平行光以${\theta }_0$角斜入射在宽度为$a$的单缝上时，考虑光屏上角位置为$\theta$的点，其光程差由经过单缝前后的两段路径分别贡献

$$\Delta L=\Delta L_0+\Delta L_1=-a\sin {\theta }_0+a\sin \theta =a\left(\sin \theta -\sin {\theta }_0\right)$$

这时候

1. 强度公式基本不变

$$I(\theta )=I(0)\left(\frac{\sin \alpha }{\alpha }\right)$$

只需要我们修正$\alpha$的定义为

$$\alpha =\frac{\pi a}{\lambda }(\sin \theta -\sin {\theta }_0)$$

2. 所以零级中心的位置仍然在几何光学像点处$\theta ={\theta }_0$，而对于$k$级亮纹则有

$$\sin {\theta }_k-\sin {\theta }_0=\left(k+\frac{1}{2}\right)\frac{\lambda }{a}⟹\sin {\theta }_k=\sin {\theta }_0+\left(k+\frac{1}{2}\right)\frac{\lambda }{a}$$

3. 于是可以计算$k$级亮纹的角宽度（注意由于${\theta }_0$的存在我们无法假设$\theta \to 0$）

$$\frac{\lambda }{a}=\Delta (\sin {\theta }_k)=\cos {\theta }_k\Delta {\theta }_k⟹\Delta {\theta }_k=\frac{\lambda }{a\cos {\theta }_k}(k\ne 0)$$

特别地当$k=0$时，$\Delta {\theta }_0=\frac{2\lambda }{a\cos {\theta }_0}$，其对于的半角宽就是$\frac{\lambda }{a\cos {\theta }_0}$

如果衍射屏前后两侧为不同介质，设前场照明空间折射率为$n_1$，后场衍射空间折射率为$n_2$，则光程差变为$\Delta L=a(n_2\sin \theta -n_1\sin {\theta }_0)$，从而有强度公式

$$I(\theta )=I(0)\left(\frac{\sin \alpha }{\alpha }\right),\alpha =\frac{\pi a}{{\lambda }_0}(n_2\sin \theta -n_1\sin {\theta }_0)$$

其中${\lambda }_0$表示衍射光在真空中的波长，注意这里零级亮纹的位置${\theta }_0^{\prime }$需要满足

$$\alpha =0⟹n_2\sin {\theta }_0^{\prime }-n_1\sin {\theta }_0=0$$

即${\theta }_0^{\prime }$为斜入射光源通过衍射屏后的折射角，而其他级亮条纹的位置为

$$n_2\sin {\theta }_k-n_1\sin {\theta }_0=\left(k+\frac{1}{2}\right)\frac{{\lambda }_0}{a}⟹\sin {\theta }_k=\frac{n_1}{n_2}\sin {\theta }_0+\left(k+\frac{1}{2}\right)\frac{{\lambda }_0}{n_{2}a}$$

它们的角宽度

$$\Delta {\theta }_k=\frac{{\lambda }_0}{n_{2}a\cos {\theta }_k}(k\ne 0)$$

特别地对于零级条纹，其角宽度

$$\Delta {\theta }_0^{\prime }=\frac{2{\lambda }_0}{n_{2}a\cos {\theta }_0^{\prime }}=\frac{2{\lambda }_0}{a\sqrt{n_2^2-n_1^2{\sin }^2{\theta }_0}}$$

只有它半角宽才和其他的条纹有一样的形式，即$\frac{{\lambda }_0}{a\sqrt{n_2^2-n_1^2{\sin }^2{\theta }_0}}$

光学仪器的分辨本领

Airy斑

通过求解Fresnel积分我们可以得到Frauhofer圆孔衍射下（前面讨论的都是二维的情况）主极大的半角宽

$$\Delta {\theta }_0=0.61\frac{\lambda }{a}=1.22\frac{\lambda }{D}$$

这个主极大的光斑被称为Airy斑，其中$D$为衍射孔的直径

相机的光圈数

相机的光圈数定义为镜头焦距和最大光圈直径的比值，即$\frac{f}{D}$. 例如，如果镜头的最大光圈直径是$10$mm,焦距是$50$mm，那么光圈数就是$50/10=5$，通常记为$f/5$

光圈数越小，表示光圈越大，进光量越多. 光圈数越大，表示光圈越小，进光量越少

标准的光圈级数为:$f/1,f/1.4,f/2,f/2.8,f/4,f/5.6,f/8,f/11,f/16,f/22,f/32$. 这些数值是相邻级数的二倍关系

Rayleigh判据

望远镜的像分辨能力

当一个圆斑像的中心刚好落在另一圆斑像的边缘（第一暗纹）上时，被认为刚刚能被分辨. 由此定义的最小分辨角为：

$$\delta {\theta }_m=1.22\frac{\lambda }{D}$$

由此可知，如果要提高望远镜的分辨本领，光提升它的放大率是无效的，因为它在放大像的同时把衍射光斑也一起放大了. 所以要提升望远镜的分辨率，最有效的方法是增大它物镜的口径

另一方面，望远镜的放大率太小显然也是不行的，因为这将无法最大地利用它的分辨本领. 因此，我们在选择目镜时，需要能使总放大率能将仪器的最小分辨角放大到人眼所能分辨的最小角度$1^{\prime }\approx 2.9\times 10^{-4}\mathrm{rad}$，由此我们可以定义望远镜的有效视角放大率

$$M_m=\frac{\delta {\theta }_e}{\delta {\theta }_m}$$

回忆

望远镜的放大率公式为

$$M=\frac{f_O}{f_E}$$

显微镜的像分辨能力

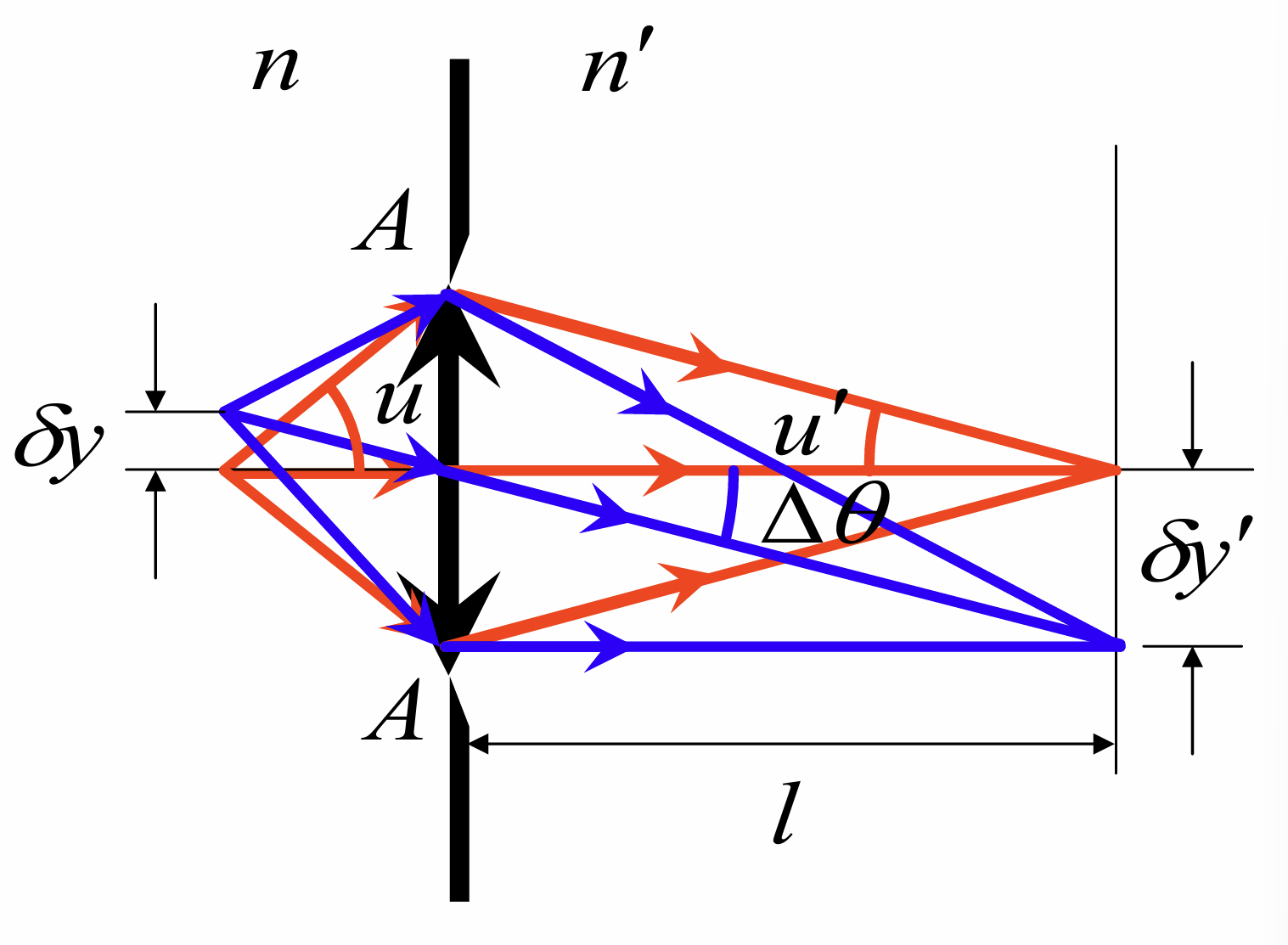显微镜的最小分辨距离为

$$\delta y_m=\frac{0.61\lambda }{n\sin u}=0.61\frac{\lambda }{N.A.}$$

其中$N.A.=n\sin u$称为显微镜的数值孔径，这里不取$1.22$而取$0.61$是因为$y$表示某处像点和中心点的距离，对应于Airy斑的半径. 由此我们可以给出提升显微镜分辨本领的方法

• 可以通过油浸增大显微镜的数值孔径，从而提升它的分辨能力
• 也可以通过使用短波长的光来提升分辨能力

由于人眼可以分辨的最小距离

$$\delta y_e=s_0\delta {\theta }_e=25\mathrm{cm}\times \left(2.9\times 10^{-4}\mathrm{rad}\right)=72.5\mu \mathrm{m}$$

故我们也可以定义显微镜的有效放大率

$$M=\frac{\delta y_e}{\delta y_m}$$

回忆

显微镜的放大率公式为

$$M=V_O{M}_E=-\frac{\Delta }{f_O}\frac{s_0}{f_E}$$

多缝衍射，$\alpha ,\beta$的定义，在特殊情况下（不均匀间距）

定义$d$为缝和缝之间的距离（即缝的空间周期），每个缝的宽度为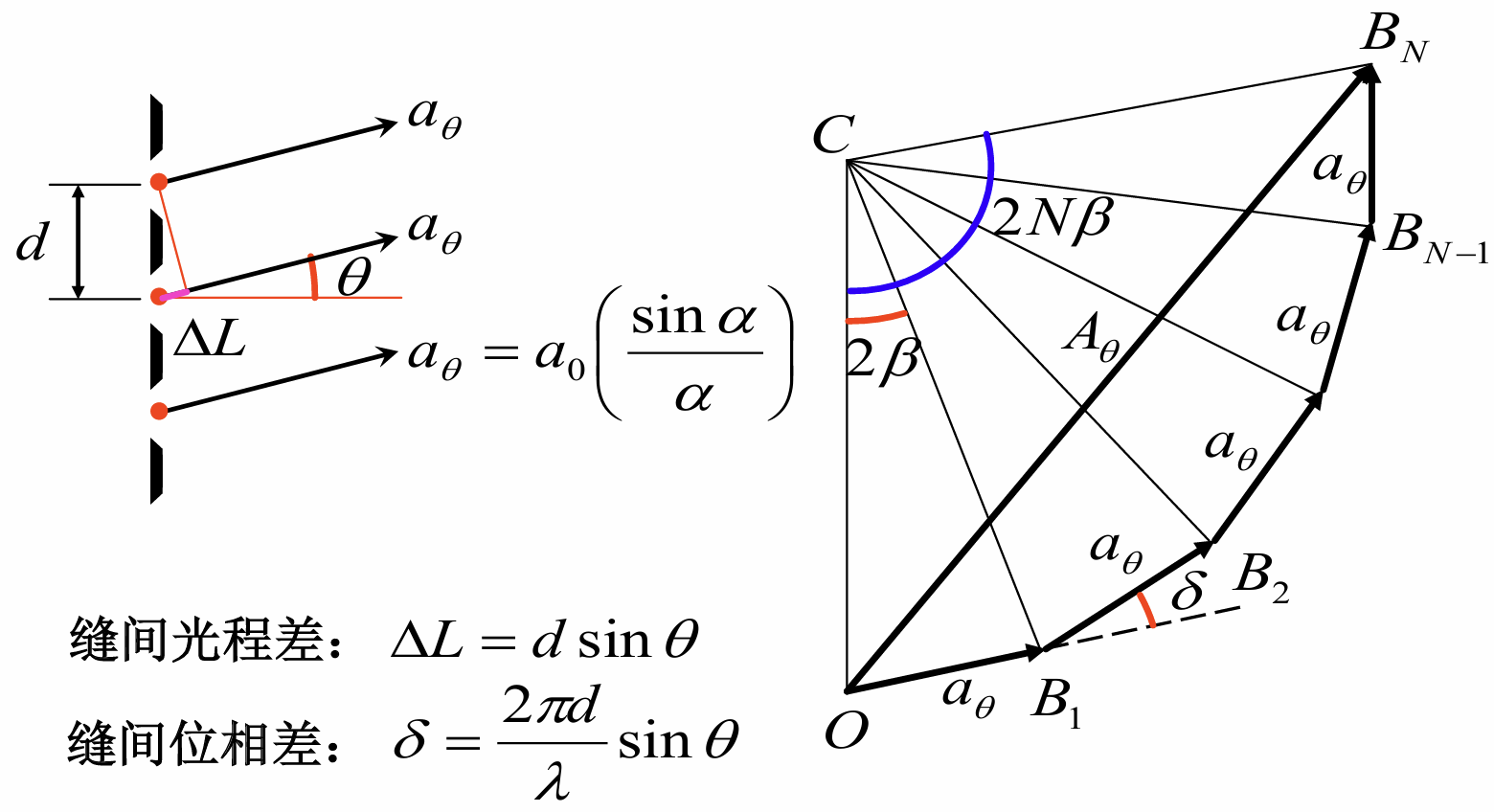$a$，考虑$\theta$处的衍射 设$\alpha =\frac{\pi a}{\lambda }\sin \theta$，则每一个缝贡献的振幅为$a_{\theta }=a_0\left(\frac{\sin \alpha }{\alpha }\right)$，而每相邻两个缝之间的的光程差为$\Delta L=d\sin \theta$，对应的相位差就是$\delta =\frac{2\pi d}{\lambda }\sin \theta$，再设$\beta =\frac{\delta }{2}=\frac{\pi d}{\lambda }\sin \theta$，则我们可以作出上面的振幅矢量合成图（假设一共有$N$个缝）

设半径$R=\overline{CO}=\overline{C{B}_N}$，则有

$$a_{\theta }=2R\sin \beta ,A_{\theta }=2R\sin N\beta ⟹A_{\theta }=a_{\theta }\frac{\sin N\beta }{\sin \beta }$$

得到光强公式

$$I_{\theta }=A_{\theta }^2=a_0^2{\left(\frac{\sin \alpha }{\alpha }\right)}^2{\left(\frac{\sin N\beta }{\beta }\right)}^2$$

其中$\left(\frac{\sin \alpha }{\alpha }\right)$为单缝衍射因子，$\left(\frac{\sin N\beta }{\sin \beta }\right)$为缝间干涉因子，它们的图像分别如下面的(a),(b)所示，(c)是它们合成后的图像 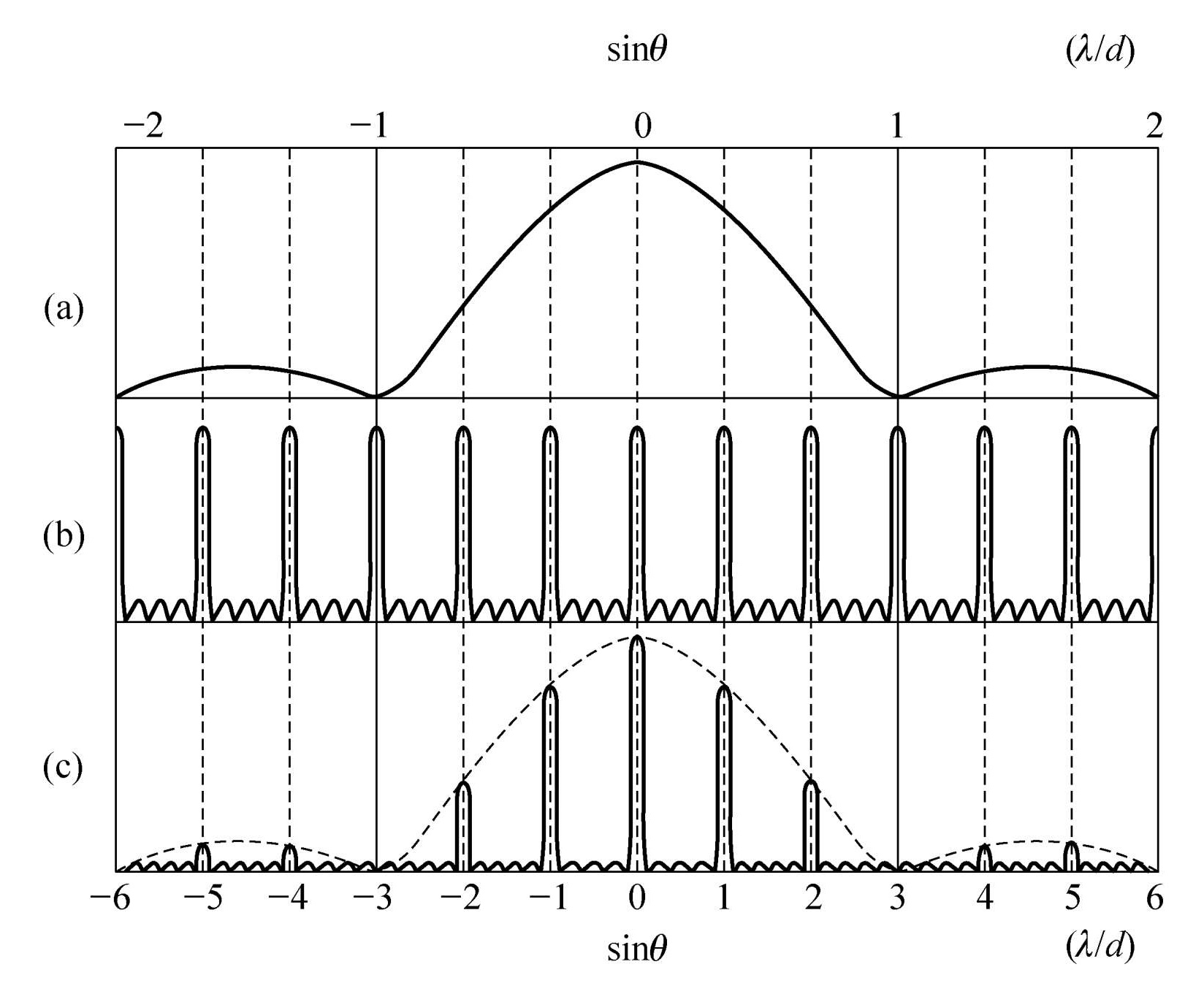一个对(c)图像的描述是

• 微观决定宏观 - 缝的大小决定图样的宏观结构（外包络）
• 宏观决定微观 - 缝和缝的间距决定图样的微观结构（每一个次极大）

类似于多缝干涉，多缝衍射的图样存在主极大（所以$\Delta L=k\lambda$的时候对应得是干涉的极大，而不是衍射的极小）

$$d\sin \theta =k\lambda ⟹\sin \theta =k\frac{\lambda }{d},k=0,\pm 1,\pm 2,\dots$$

考虑图样的暗点，也就是缝间衍射因子的零点，我们可以解得

$$\frac{\sin N\beta }{\sin \beta }=0⟹N\beta =m\pi ,\beta \ne n\pi$$

又因为$\beta =\frac{\pi d}{\lambda }\sin \theta$，所以我们得到零点的位置

$$\sin \theta =\left(k+\frac{m}{N}\right)\frac{\lambda }{d},k=0,\pm 1,\pm 2,\dots ;m=1,2,\dots ,N-1$$

其中$m=N$的情况恰好对应于主极大，每两个主极大之间有$N-1$个暗点，而每两个相邻的暗线之间都有一个次极大，也就是说每两个主极大之间都有$N-2$个次极大

因为每一个主极大不是两两紧挨的，所以我们不能采用单缝衍射中的方法来计算主极大的半角宽，而需要通过

$$\sin {\theta }_k=k\frac{\lambda }{d},\sin ({\theta }_k+\Delta {\theta }_k)=\left(k+\frac{1}{N}\right)\frac{\lambda }{d}$$

来给出

$$\Delta {\theta }_k\cos {\theta }_k=\sin ({\theta }_k+\Delta {\theta }_k)-\sin {\theta }_k=\frac{\lambda }{Nd}⟹\Delta {\theta }_k=\frac{\lambda }{Nd\cos {\theta }_k}$$

当某一个主极大恰好被单缝衍射因子调制为$0$的时候，我们称这种情况为缺级，它满足

$$\sin \theta =k\frac{\lambda }{a}=k^{\prime }\frac{\lambda }{d}$$

光栅

衍射光栅是一个重复的衍射元素阵列，可以是光圈或障碍物，其效果是产生出射波的周期性相位、幅度或两者的变化.

多缝衍射是最简单的光栅

光栅公式

$$d(\sin \alpha \pm \sin \beta )=k\lambda$$

其中

• $d$ 为光栅常数，即缝和缝之间的间距
• $\alpha$为入射角
• $\beta$为衍射角
• $k$为衍射级数

色分辨原理

色散本领

取最简单形式的光栅方程

$$d\sin {\theta }_k=k\lambda$$

有

$$d\cos {\theta }_k\frac{\delta \theta }{\delta \lambda }=k$$

于是有角色散本领

$$D_{\theta }=\frac{\delta \theta }{\delta \lambda }=\frac{k}{d\cos {\theta }_k}$$

由此我们可以定义线色散本领

$$D_l=\frac{\delta l}{\delta \lambda }=f{D}_{\theta }=\frac{kf}{d\cos {\theta }_k}$$

这里$D_l(k)$也被称为第$k$级光谱的线色散，其中$f$是聚光镜的焦距

色分辨本领

多缝衍射中给出了主极大的半角宽

$$\Delta \theta =\frac{\lambda }{Nd\cos {\theta }_k}$$

又因为$D_{\theta }=\frac{\delta \theta }{\delta \lambda }$，故我们可以定义最小分辨波长

$$\delta \lambda =\frac{\delta \theta }{D_{\theta }}=\frac{\lambda }{kN}$$

和分辨本领

$$R=\frac{\lambda }{\delta \lambda }=kN$$

也就是说，光栅缝数越多，其色分辨本领越强

Fourier光学

复习Fourier变换

见Fourier变换和光学中的Fourier变换

衍射系统和屏函数

凡是能使波前复振幅发生改变的物，统称为衍射屏 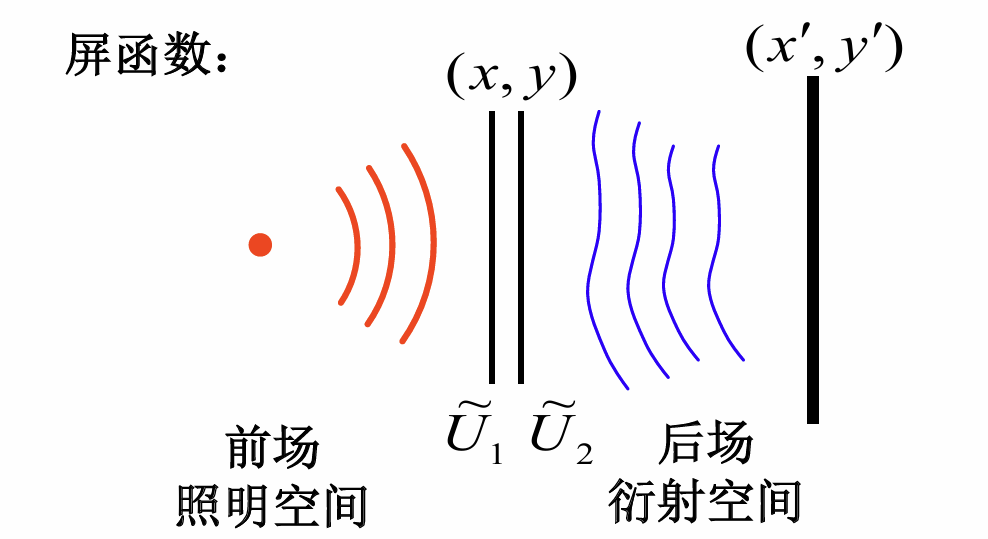定义屏函数为衍射屏前后表面对应的复振幅之比

$$\tilde{t}(x,y)=\frac{{\tilde{U}}_2(x,y)}{{\tilde{U}}_1(x,y)}$$

有接收平面上的振幅分布

$$\begin{array}{c}\tilde{U}(x^{\prime },y^{\prime })=\frac{-i}{\lambda }{\iint }_{({\Sigma }_0)}\tilde{t}(x,y)\cdot {\tilde{U}}_1(x,y)\frac{e^{ikr}}{r}dxdy\\ \ne \frac{-i}{\lambda }{\iint }_{({\Sigma }_0)}{\tilde{U}}_1(x,y)\frac{e^{ikr}}{r}dxdy\end{array}$$

由于衍射屏函数的作用，改变了波前，从而改变了后场的分布，于是发生的衍射

屏函数的分类

振幅型：$\tilde{t}(x,y)=t(x,y)$，特别地对孔或者遮光屏而言

$$t(x,y)=\{\begin{array}{ll}1& \text{透光部分}\\ 0& \text{遮光部分}\end{array}$$

对于一个理想无限小半径的圆孔屏，它的屏函数可以通过delta函数表示

$$t(x,y)=\delta (x,y)$$

位相型：$\tilde{t}(x,y)=e^{\mathrm{i}\phi (x,y)}$

正弦光栅

屏函数

$$\tilde{t}\left(x,y\right)=t_0+t_1\cos \left(q_{x}x+q_{y}y+{\phi }_0\right)$$

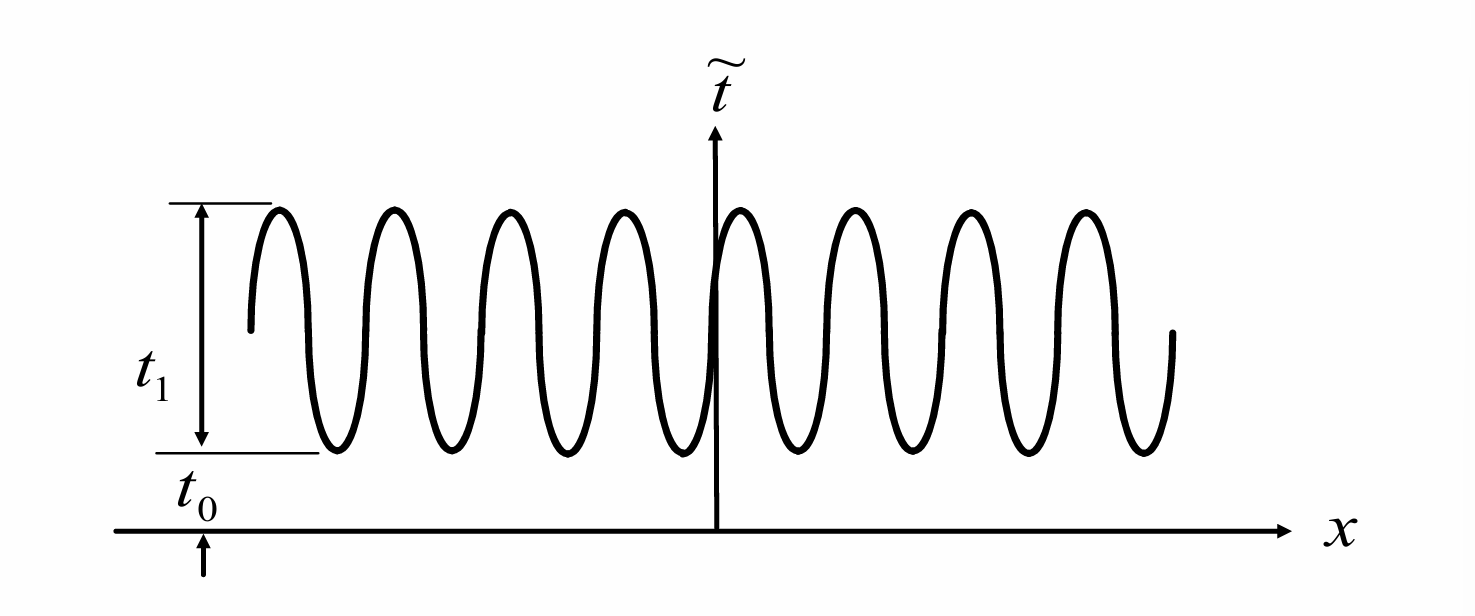
衍射图样

考虑平行光入射${\tilde{U}}_1{A}_1$

$$\begin{array}{rl}{\tilde{U}}_2(x,y)& ={\tilde{U}}_1(x,y)\tilde{t}(x,y)\\ & =A_1[t_0+t_1\cos (2\pi fx+{\phi }_0)]\\ & \begin{array}{rl}& =A_1{t}_0+A_1{t}_1\frac{e^{i(2\pi fx+{\phi }_0)}+e^{-i(2\pi fx+{\phi }_0)}}{2}\\ & ={\tilde{U}}_0(x,y)+{\tilde{U}}_{+1}(x,y)+{\tilde{U}}_{-1}(x,y)\end{array}\end{array}$$

由相因子判断出射光为三个不同方向的平面波，其中$\sin {\theta }_{\pm 1}=\pm f\lambda$

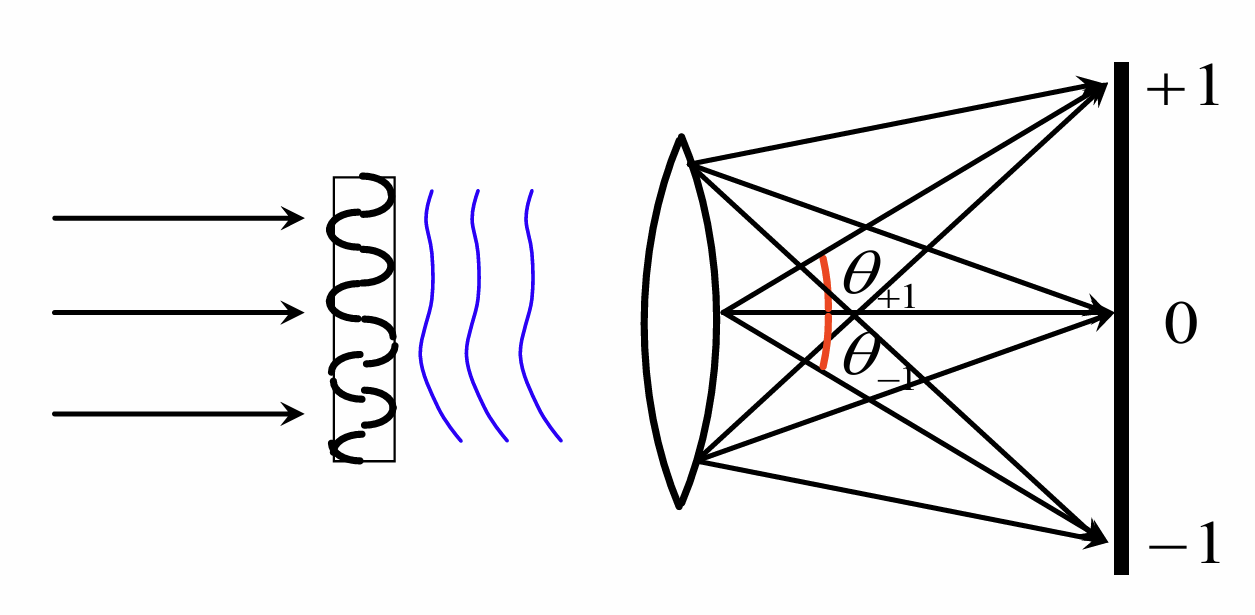
任意光栅的屏函数

利用Fourier展开把任意光栅的屏函数展开为正弦光栅的屏函数的叠加

$$\begin{array}{rl}\tilde{t}\left(x\right)& =\sum _{n=-\infty }^{\infty }{\tilde{t}}_n{e}^{i2\pi nfx}\\ & \\ \text{where}{\tilde{t}}_n& =\frac{1}{d}{\int }_{-d/2}^{d/2}\tilde{t}\left(x\right)e^{-i2\pi nfx}dx\end{array}$$

解释Fraunhofer衍射

光屏上一点接受到的电场振幅可以写成一个对衍射屏的积分

$$E(Y,Z)=\iint \mathcal{A}(y,z)e^{ik(Yy+Zz)/R}\mathrm{d}y\mathrm{d}z$$

其中屏函数包含振幅衰减因子和相位改变因子两项

$$\mathcal{A}(y,z)={\mathcal{A}}_0(y,z)e^{i\varphi (y,z)}$$

分析衍射屏上每一个$\mathrm{d}y\mathrm{d}z$面元在光屏上某点$P(Y,Z)$贡献的振幅，可以看做是由一列沿着$\mathbf{k}$方向（即$(0,0)\to (Y,Z)$方向）传播的振幅为$\mathcal{A}(y,z)\mathrm{d}y\mathrm{d}z$平面波贡献的（在远场条件下，光屏接收到的光波才能被视为平面波；又因为光屏足够远，尺度也远大于像小孔这样的衍射屏，所以只要接受的位置确定，衍射屏上的每一个面元产生的平面波都可以看作拥有一样的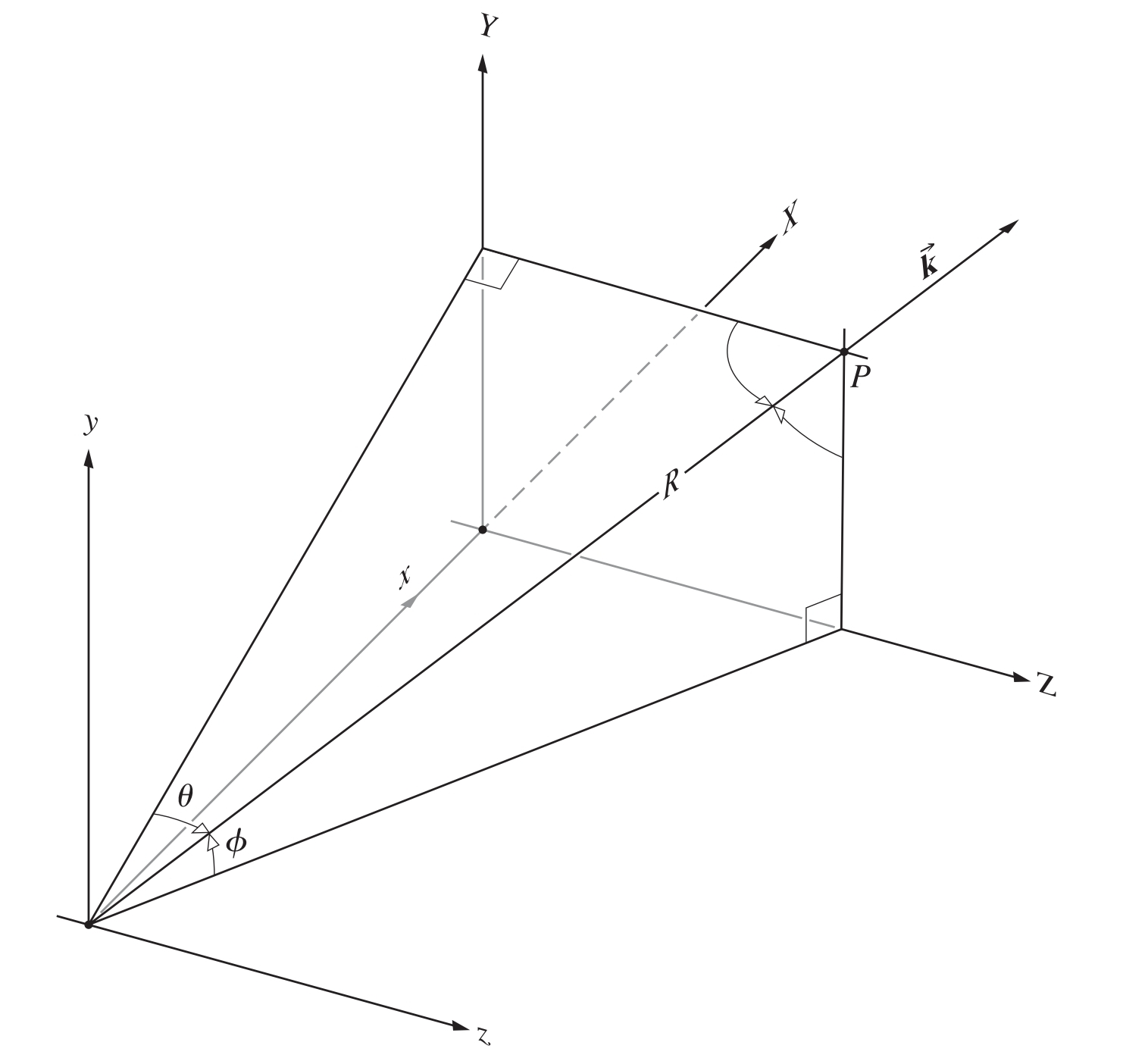$\mathbf{k}$） 由上图中的几何关系，我们可以定义角度空间频率$k_Y,k_Z$为

$$k_Y:=\frac{kY}{R}=k\sin \varphi ;k_Z:=\frac{kZ}{R}=k\sin \theta$$

光屏上的每一个点都有一个对应一对空间频率，由此衍射场就可以被写成

$$E(k_Y,k_Z)=\iint \mathcal{A}(y,z)e^{i(k_{Y}y+k_{Z}z)}\mathrm{d}y\mathrm{d}z$$

这个形式和上文中的二维Fourier变换中的形式是一致的，所以可以被写成

$$E(k_Y,k_Z)=\mathcal{F}\left\{\mathcal{A}(y,z)\right\}$$

这指出了Fraunhofer衍射的衍射场分布就是屏函数的Fourier变换

同理我们可以通过Fourier逆变换求出屏函数

$$\mathcal{A}(y,z)={\mathcal{F}}^{-1}\left\{E(k_Y,k_Z)\right\}$$

从上文的Fourier变换的性质中我们知道，信号的宽度越窄，它的Fourier变换就越宽，这在二维情况下也成立，表现在衍射中就是衍射空越窄，屏函数的信号宽度也越窄，衍射光束和相应的条纹也就越宽

在实际情况下，我们不可能在无穷远处放置屏幕来观察衍射图样. 通常，我们会在一个有限距离处放置屏幕. 在这种情况下，观察到的电场分布和理想的Fraunhofer衍射电场分布相比，会有非常小的相位差异. 这是因为在有限距离处，光波前还不能完全被看作平面波，仍有一定的曲率，导致相位的微小变化.

这个相位差异在大多数情况下并不显著，尤其是对于我们实际观测的辐照度（光强）来说. 辐照度只与电场幅度的平方成正比，而相位差异不影响电场幅度，因此我们在有限距离处观察到的衍射图样在强度分布上与理想的Fraunhofer衍射几乎一致.

Abbe成像原理

Abbe成像理论

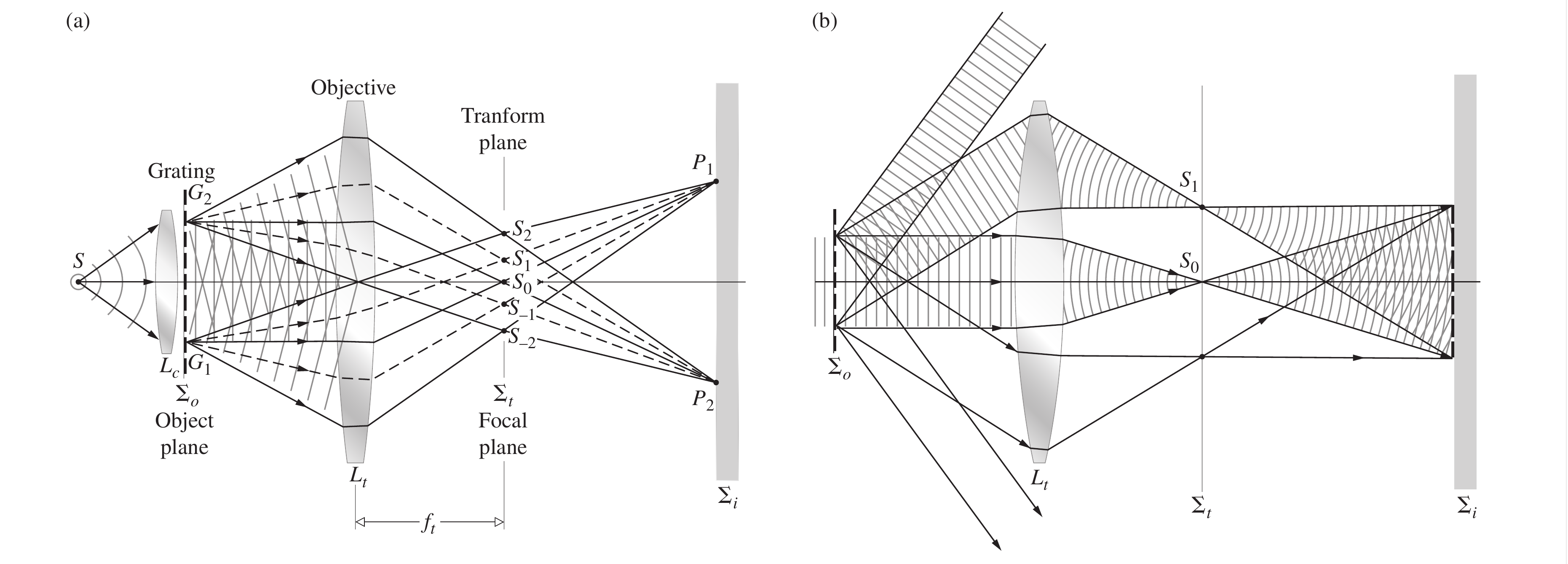
考虑上图的光学系统$(a)$，准直透镜($L_c$)发射出平面单色波，这些波前被光栅衍射. 衍射后的波前变得扭曲，我们将其解析为一组新的平面波，每个波对应一个特定的级数$m=0,\pm 1,\pm 2,...$或空间频率，并且沿特定方向传播，就如$(b)$中所示的那样

物镜$(L_t)$是变换透镜，在${\Sigma }_t$（也就是$L_t$的后焦面）上形成Fraunhofer衍射图样. 这些波通过${\Sigma }_t$后到达像平面${\Sigma }_i$后将重叠并相互干涉，形成光栅的倒立图像（例如坐标的$G_1,G_2$分别成像在$P_1,P_2$）.

在这个光学系统中两个值得关注的图样，一个是源$S$所在平面的共轭${\Sigma }_t$上的由Fourier变换形成的图样，另一个是物平面的共轭${\Sigma }_i$上的图像.

下图是采取平面单色光源照明一个单缝时物平面和上述两个平面上的振幅分布 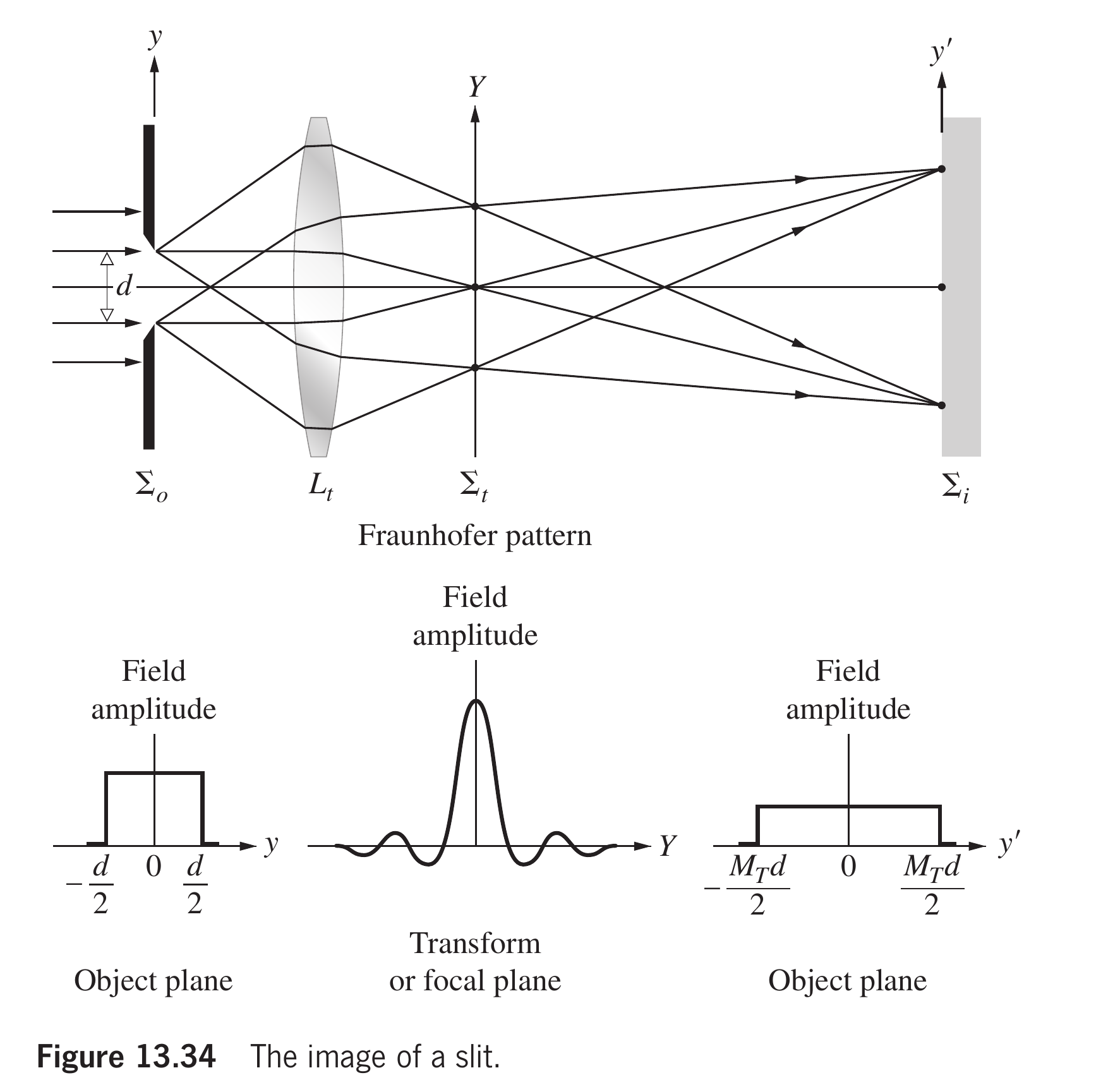这些系统最初是在$1873$年由Ernst Abbe$(1840-1905)$提出的. 当时他的兴趣集中在显微镜理论的研究上. 如果我们把$L_t$视为显微镜的物镜，那么它与上述讨论的联系就很明显了. 此外，如果将光栅替换为一块薄薄的半透明材料（即待检测的样本），并用来自小光源和聚光器的光线照亮，这个系统显然与显微镜非常相似.

Carl Zeiss$(1816-1888)$在19世纪中叶经营着Jena的一间小型显微镜工厂，他认识到当时显微镜发展过程中试错法的局限性. $1866$年，他邀请了当时在Jena大学任讲师的Ernst Abbe，共同探索一种更科学的显微镜设计方法. Abbe通过实验发现，即使入射光锥只占物镜的一小部分，较大的孔径也能带来更高的分辨率，周围的“暗空间”似乎对成像有所贡献. 因此，他提出了一种观点：在镜头边缘发生的衍射过程（对于点光源产生Airy图案）并不像非相干照明的望远镜物镜那样起作用. 大小与$l$相当的标本显然是将光线散射到显微镜物镜的“暗空间”中. 观察图$b$，如果物镜的孔径不足以收集所有衍射光，则图像并不完全对应于原物体. 相反，它与一个虚构的物体有关，其完整的衍射图案与$L_t$收集的图案相匹配.

实际上，除非物镜具有无限大的孔径，否则它作为一个低通滤波器，会拒绝超过某一特定值的空间频率（也就是截止频率），并允许所有低于该值的频率通过（前者是那些超出镜头物理边界的频率）. 因此，所有实际镜头系统在相干照明下复制实际物体的高空间频率内容的能力都将受限

在下面的系统中，我们将解释Abbe成像原理将平行相干光照明透镜成像分成了两步

1. 物平面发生Fraunhofer衍射，在透镜像方焦面上形成的衍射图样是物平面的空间频谱
2. 频谱面上的各衍射斑发出的次波在像平面上干涉，形成的图样即为像

空间滤波和4F系统

在Abbe光学系统中，如果去除准直透镜$L_c$，那么在$L_t$的左焦平面${\Sigma }_0$上发射的光将会在无穷远处汇聚，这时候我们也可以类似地引入成像透镜$L_i$使得

• $L_t$让衍射图样成在有限远处
• $L_i$让物的像成在有限远处 事实上，这个成像透镜也实现了一个Fourier变换，可以把它的作用看作把${\Sigma }_t$上的衍射图样再次作逆Fourier变换呈现到${\Sigma }_i$上

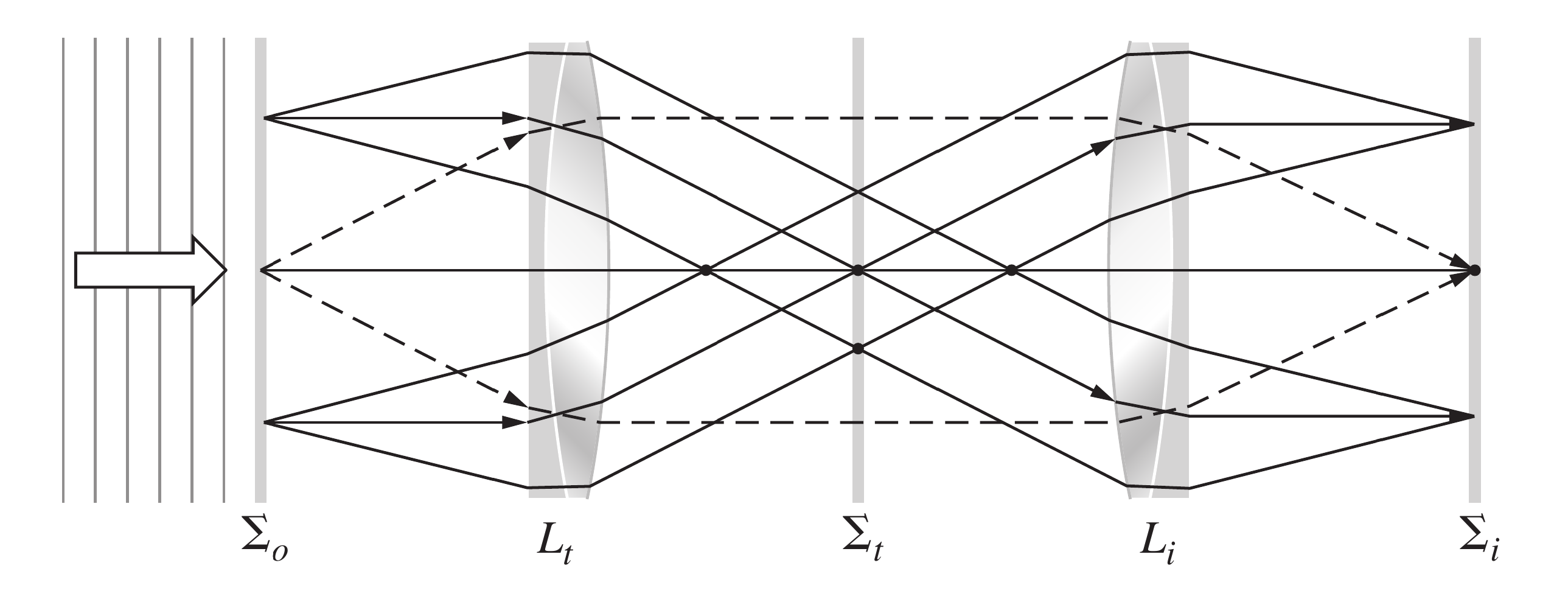如下图，我们常常取$f_t=f_i$，这个光学系统被称为4F系统 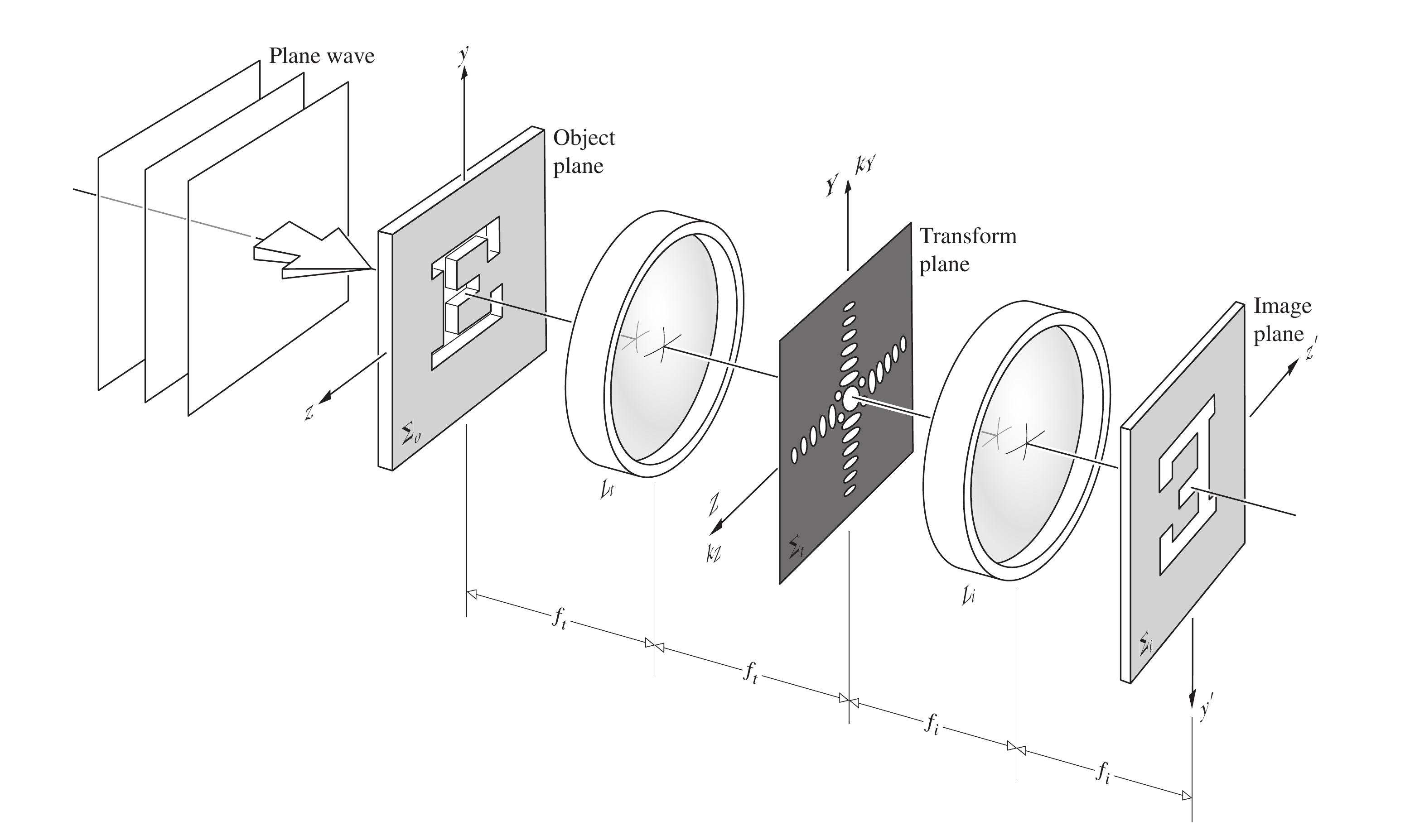我们可以通过在${\Sigma }_t$上设置遮光屏来控制对应频率分量的通过性，从而实现操作图像的目的，这种操作也被称为空间滤波

振幅分布的计算

如果的变换屏的屏函数$t(x,y)\equiv 1$，整个系统就是对物的波前${\tilde{U}}_o(x,y)$作了两次Fourier变换，数学推导和物理分析都告诉我们

$${\tilde{U}}_i(x^{\prime },y^{\prime })=\mathcal{F}\left\{\mathcal{F}\left\{{\tilde{U}}_0(x,y)\right\}\right\}\propto \tilde{U}(-x^{\prime },-y^{\prime })$$

这说明连续两次的Fourier变换不改变函数的形式，只是自变量的符号改变，也就是图像倒置. 所以这个过程也可以看作为一次Fourier变换，然后再一次逆Fourier变换并倒置图像

但是在有滤波器的情况下，在频谱面上有

$${\tilde{U}}_{t2}=\tilde{t}\cdot {\tilde{U}}_{t1}$$

这时候经过第二次Fourier变换后，函数形式不再是复原加图像倒置，但是我们仍然可以对${\tilde{U}}_{t2}$作Fourier逆变换，然后倒置图像，由此来代替第二次Fourier变换的运算.

晶体光学

双折射

o光和e光

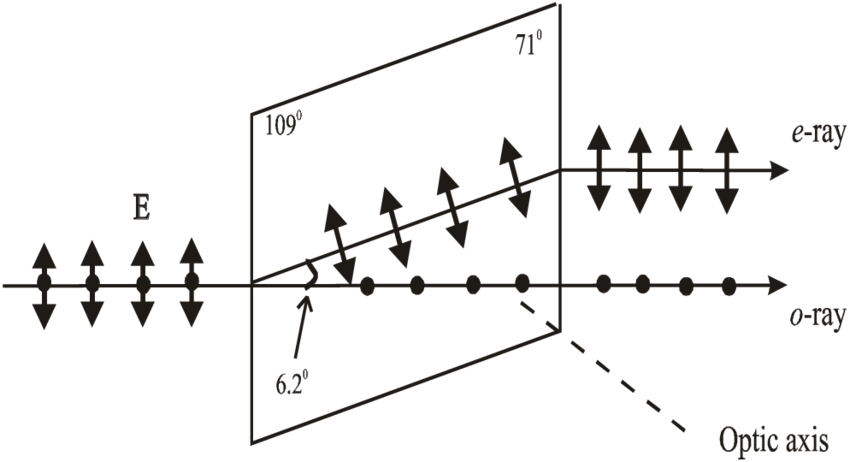让一束平行的自然光正入射在冰洲石晶体的一个表面上，我们就会发现光束分解成两束，其中一束光遵循折射定律，称为寻常光(ordinary ray, o光)，另一束会违背它，称为非常光(extraordinary ray, e光). 应当注意，o光和e光只有在双折射晶体内部有意义，射出晶体后就无所谓o光和e光了

晶体的光轴

在冰洲石中存在一个特殊的方向，光线沿着这个方向传播时o光和e光不分开（即它们的传播速度和传播方向都一样），这个特殊的方向（不是一条特殊的线）称为晶体的光轴.

主截面

当光线沿着晶体的某个界面入射时，此界面的法线和晶体的光轴组成的平面称为主截面. 只有入射线在主截面内，也就是入射面与主截面重合时，才能保证e光也在入射面内

双折射光的偏振

o光和e光都是线偏振光，且它们的振动方向相互垂直

单轴晶体中的波面

双折射晶体分为两类，只有一个光轴方向的称为单轴晶体；有两个光轴方向的称为双轴晶体

我们知道，在各向同性介质中的一个点光源发出的波沿各个方向的传播速度都是$v=\frac{c}{n}$，经过某段时间$\Delta t$后形成的波面是一个半径为$v\Delta t$的球面

在单轴晶体中的o光传播规律与普通各向同性介质中意义，其波面也是球面. 但是e光沿各个方向的传播速度不同，沿光轴方向的速度和o光一样，也就是$v_o$. 垂直光轴方向的传播速度是另一个数值$v_e$. 在经过$\Delta t$时间后e光的波面就是一个椭球. 把两个波面画在一起，它们在光轴方向上相切.

为了说明o光和e光的偏振方向，我们引入主平面的概念. 晶体中某条光线与晶体光轴构成的平面叫做主平面，下面左边图中的纸面就是图中所画光线的主平面 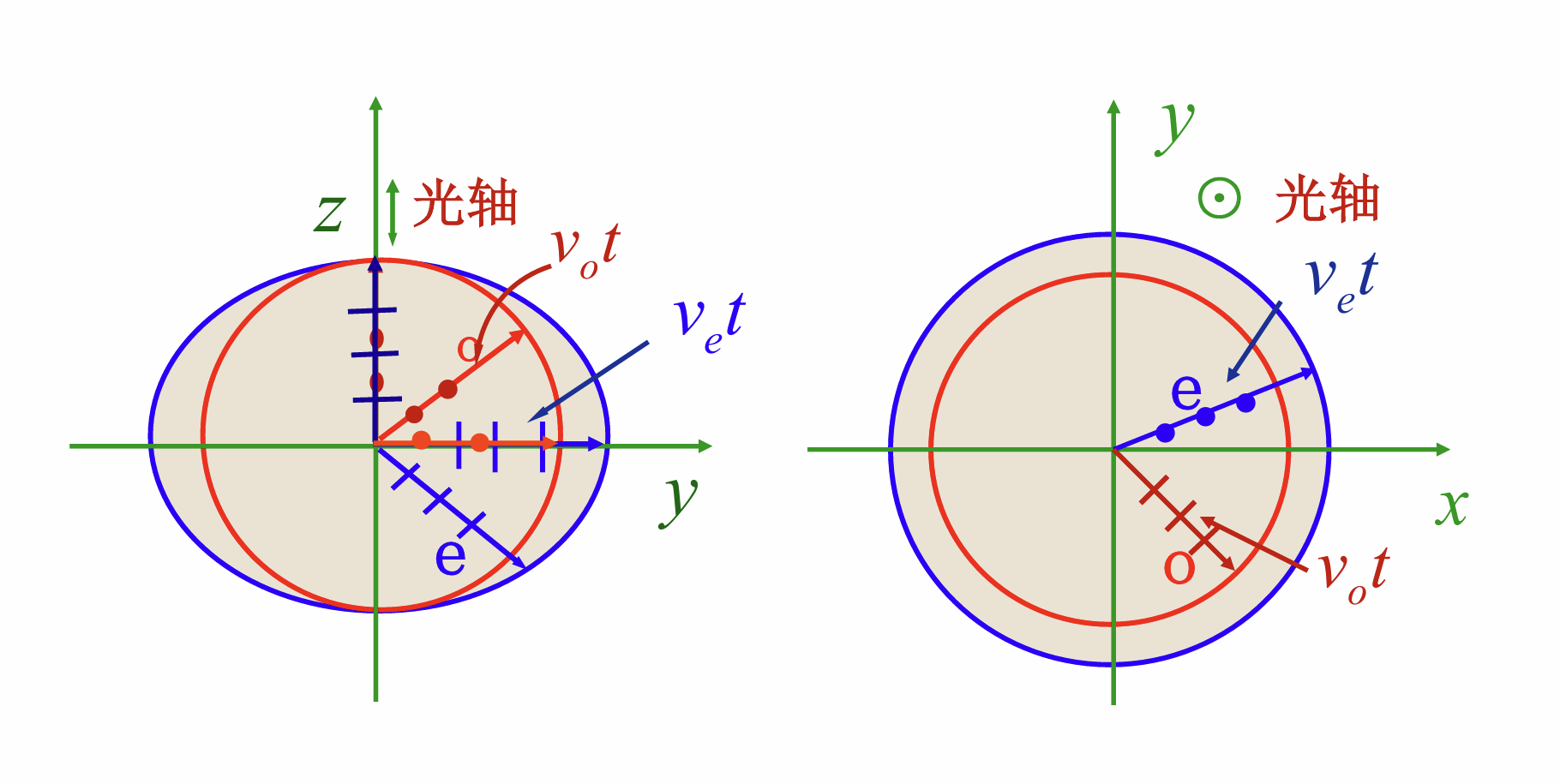o光电矢量的振动方向和主平面垂直，e光电矢量的振动方向和主平面平行，故若入射光是振动方向和主平面夹角为$\theta$的、振幅为$A$的线偏振光，那么它的振动矢量就可以分解为两个方向

$$A_e=A\cos \theta ,A_o=A\sin \theta$$

Tip

需要注意的是，如果要求光强，则和折射率有关 $I_o=n_o{A}_o^2,I_e=n_e(\varphi )A_e^2$ 其中$n_e$和入射光和光轴的夹角$\varphi$有关

单轴晶体分为两类：一类以冰洲石为代表，$v_e>v_o$，称为负晶体；另一类以石英为代表，$v_o>v_e$，称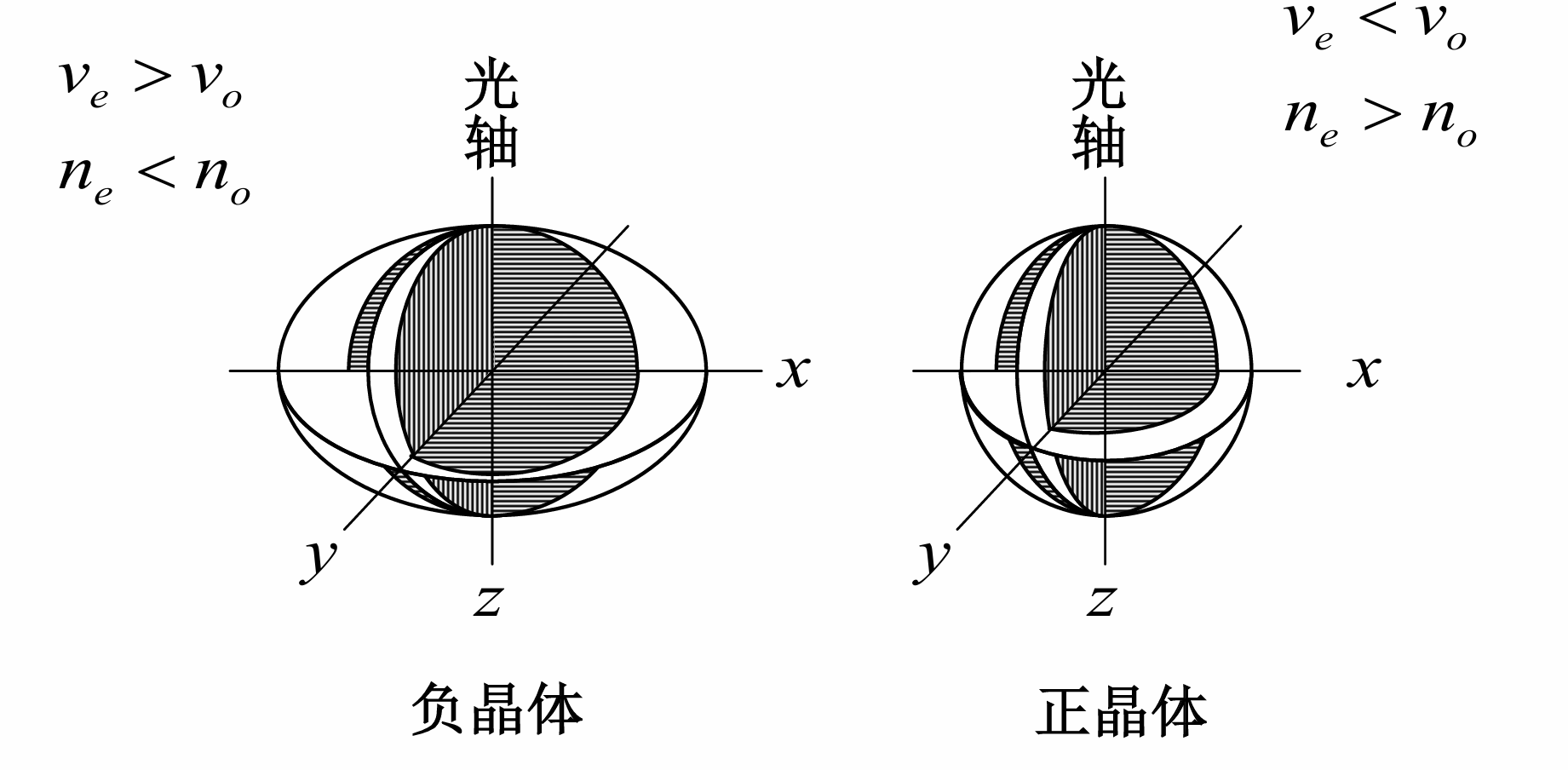为正晶体 对于e光，由于它不符合普通的折射定律，所以我们不能用一个简单的折射率来反映它的折射规律. 但是我们通常仍然把真空光速和e光沿垂直于光轴传播时候的速度之比叫做它的折射率$n_e=\frac{c}{v_e}$. 这个$n_e$虽然不具备普通折射率的含义，但它和$n_o$一样都是晶体的一个重要光学参量，我们称它们为晶体的主折射率

晶体的Huggens作图法

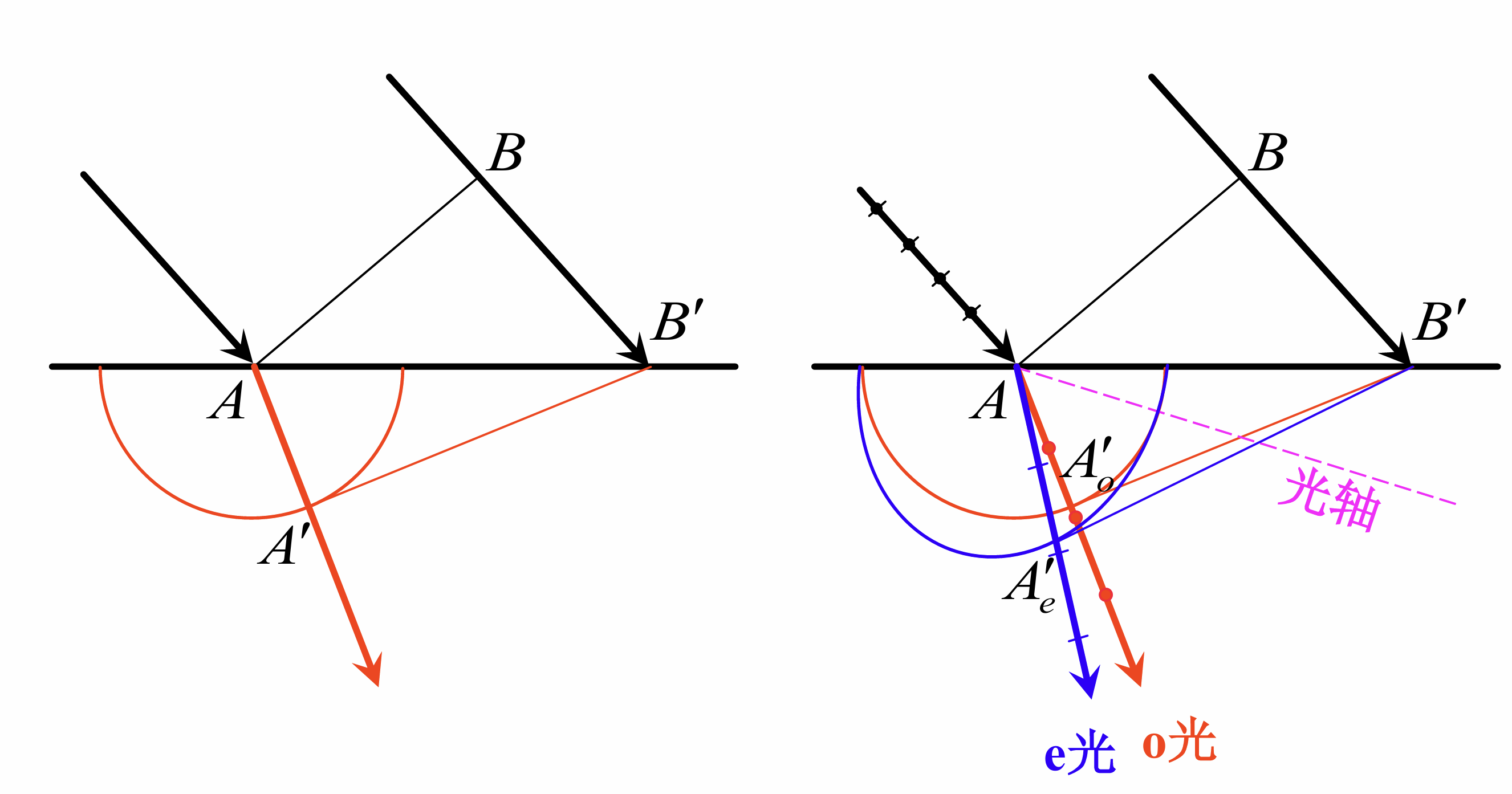具体步骤为

1. 画出平行的入射光束，令两边缘光线和界面的交点为$A,B^{\prime }$
2. 由先到界面的$A$点作另一边边缘入射线的垂线$AB$，它便是入射光的波面，求出$B$到$B^{\prime }$的时间$t=\frac{\overline{B{B}^{\prime }}}{c}$
3. 以$A$为中心，$vt$为半径在折射介质内作半圆，这就是另一边缘入射线到达$B^{\prime }$点时由$A$点发出的次波面；同时作以$A$为中心，和半圆在光轴方向相切，且另一半主轴长为$v_{e}t$的一个半椭圆
4. 通过$B^{\prime }$点作上述半圆的切线，这就是o光的波面；作上述半椭圆面的切线，这就是e光的波面

几个重要的特例

光轴垂直于界面，正入射

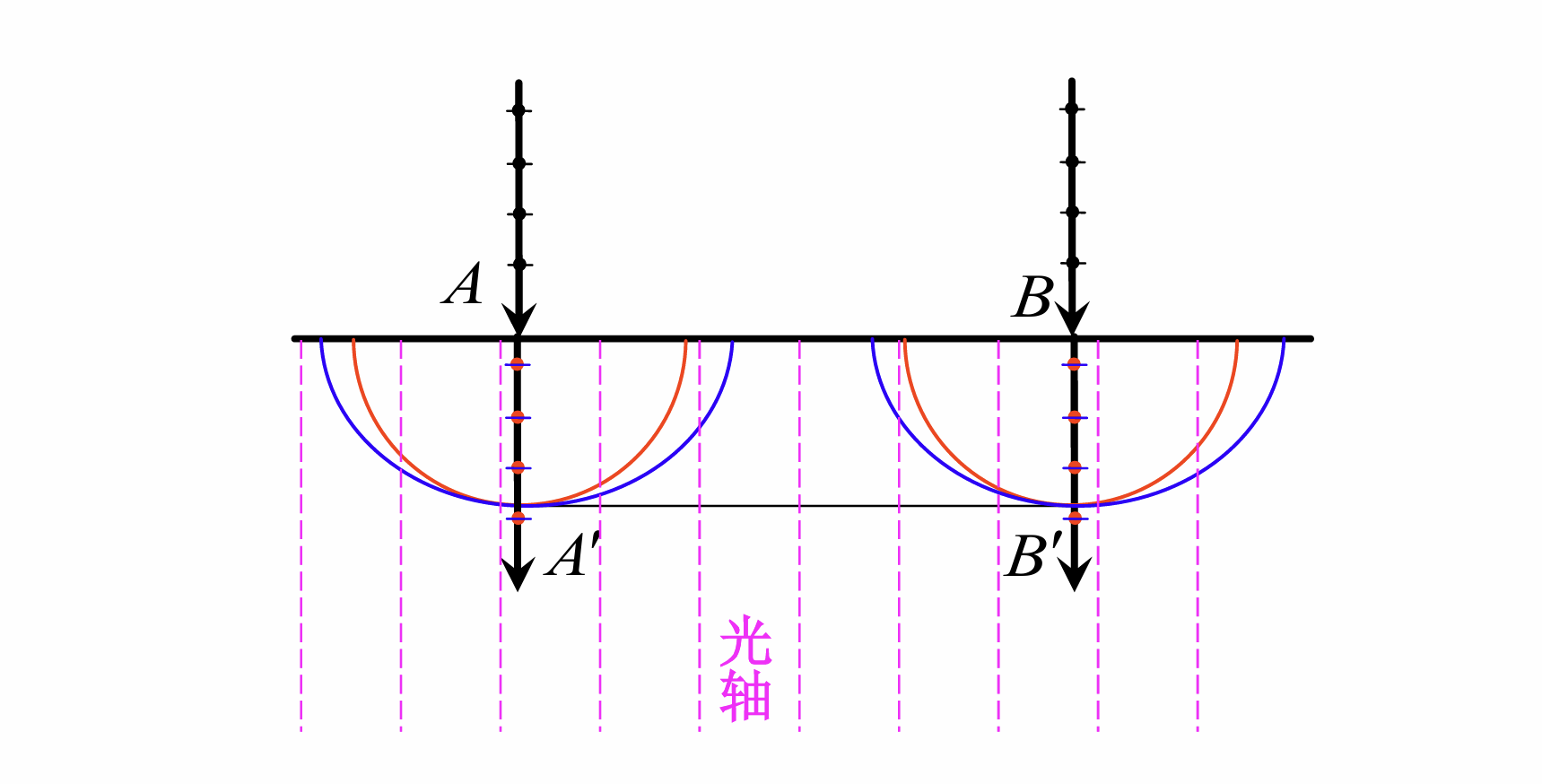
光轴平行于界面，正入射

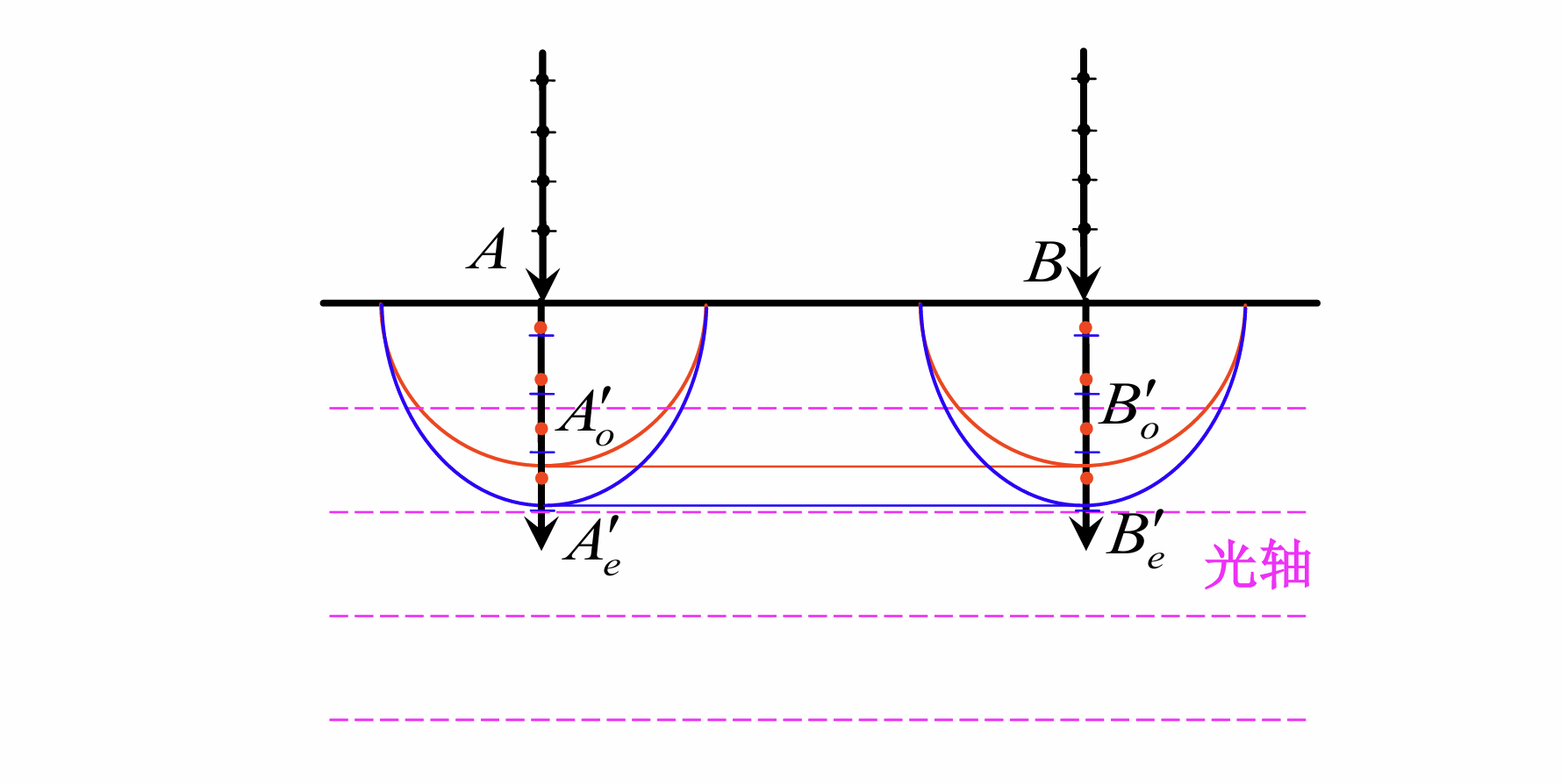
光轴垂直于界面，正入射

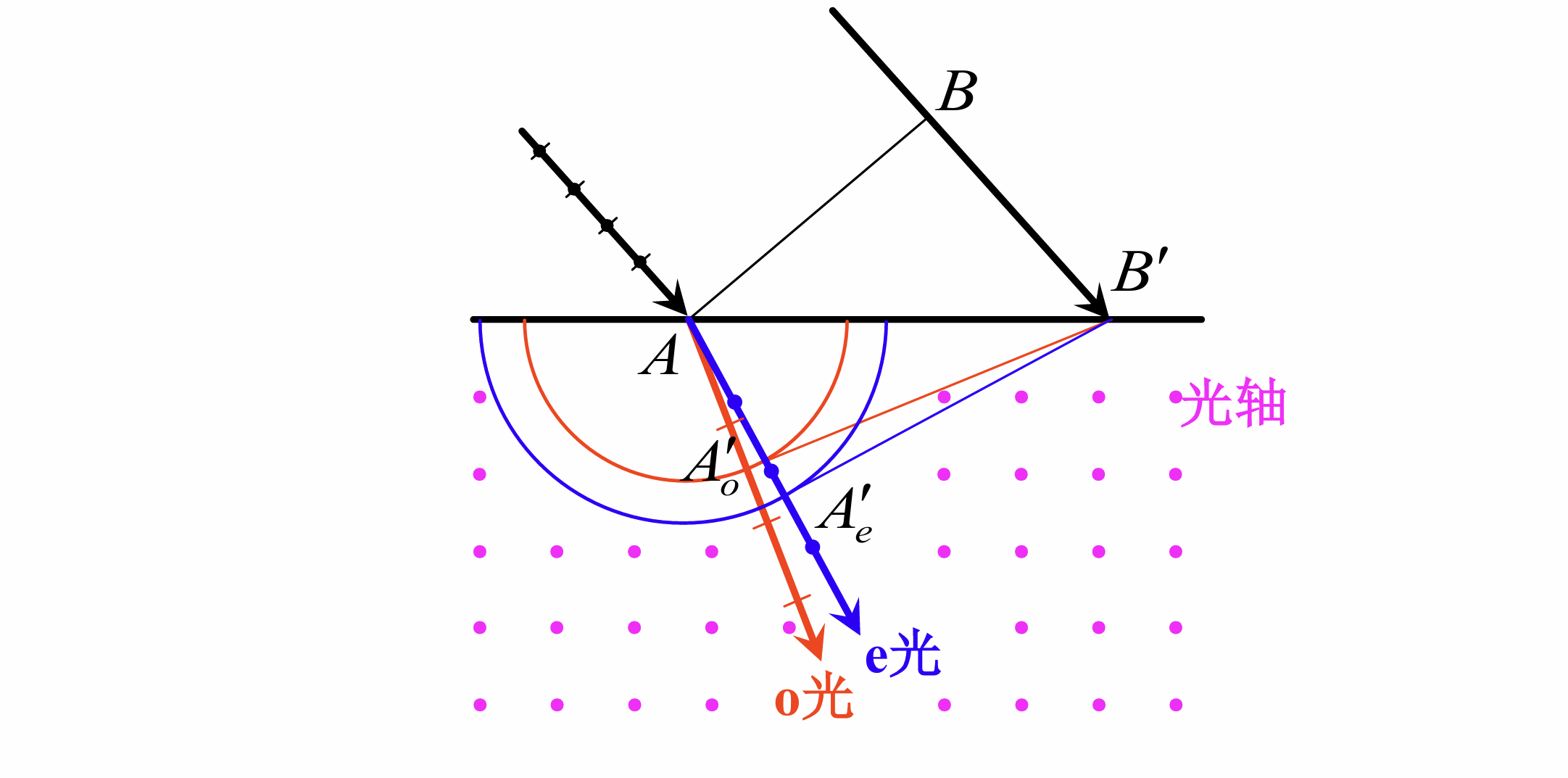此时有

$$n\sin \theta =n_o\sin {\theta }_o=n_e\sin {\theta }_e$$

晶体光学器件

晶体偏振器

利用双折射将两种偏振分开

Rochon棱镜

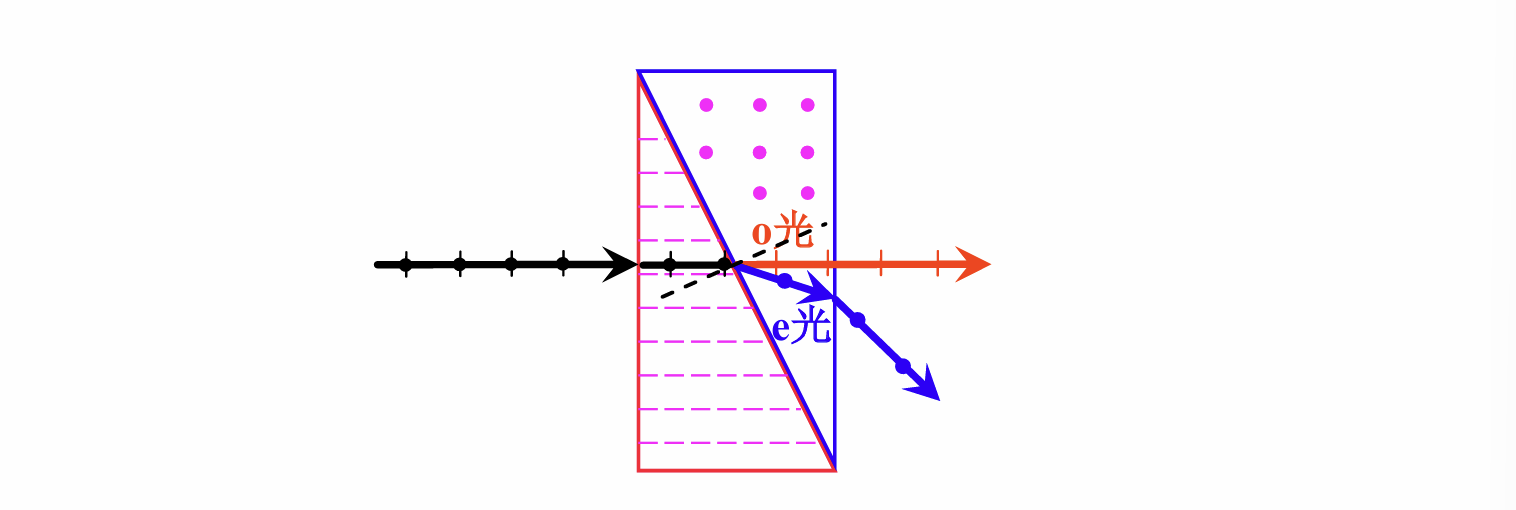对角面两边是同一种双折射介质，但是光轴的方向相互垂直；自然光入射，进入左边的棱镜后由于传播方向和光轴平行，故各方向的振动分量的折射率均为$n_o$. 越过对角面后，平行于纸面的分量垂直于新的主平面，故其折射率仍然为$n_o$，从而不发生不折射，成为继续传播的o光；而垂直于纸面的分量则平行于新的主平面，其折射率变为$n_e$，故发生折射形成e光

Wollaston棱镜

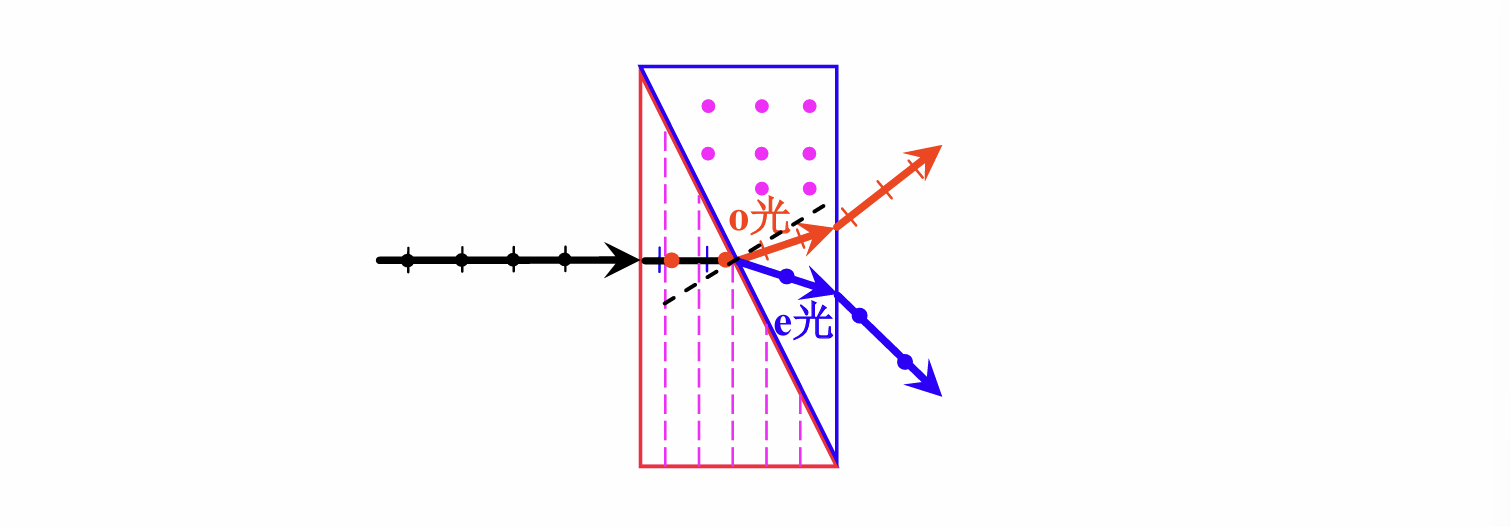对角面两边是同一种双折射介质，但是光轴的方向相互垂直；入射，进入左边的棱镜后由于传播方向和光轴垂直，平行于纸面的振动分量的折射率为$n_e$，垂直于纸面的振动分量的折射率为$n_o$. 越过对角面后，平行于纸面的分量垂直于新的主平面，其折射率变为为$n_o$，故发生折射形成o光；而垂直于纸面的分量则平行于新的主平面，其折射率变为$n_e$，故发生折射形成e光

Nicol棱镜

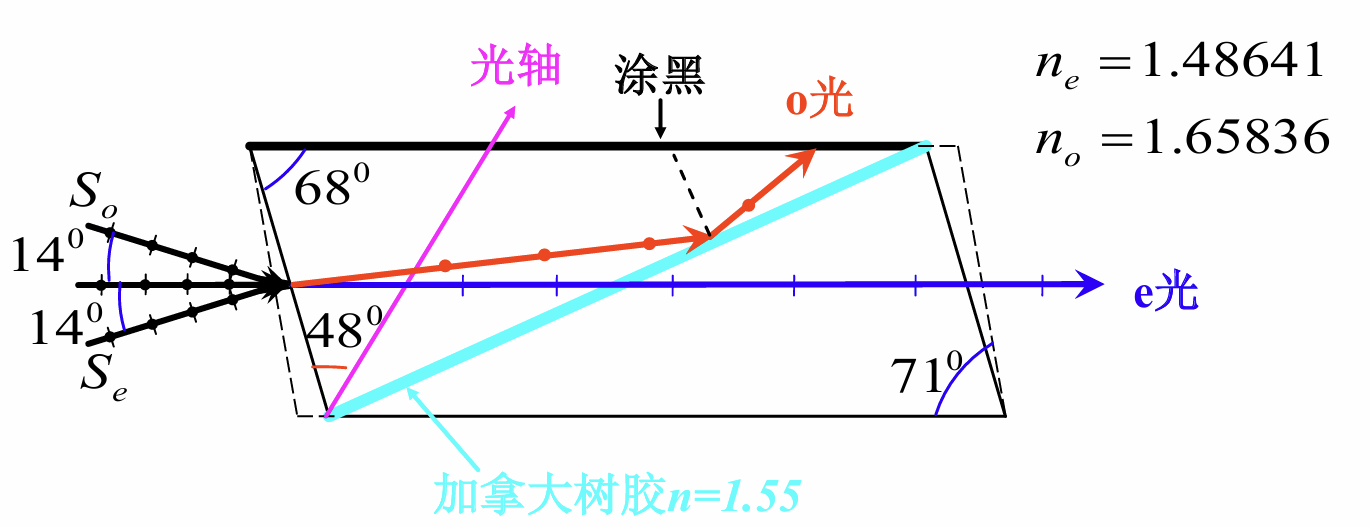其中o光在加拿大树胶面上恰好发生全发射，从而偏离光路；而e光则保持传播路径，最后射出. Nicol棱镜常被用来得到线偏振光

圆偏振光和椭圆偏振光的获得和检验

垂直振动的合成

$$\{\begin{array}{l}{E}_x=A_x\cos \omega t\\ E_y=A_y\cos (\omega t+\delta )\end{array}$$

1. $\delta =0,\pi$ 为线偏振光
2. $\delta =\pm \frac{\pi }{2}⟹\frac{E_x^2}{A_x^2}+\frac{E_y^2}{A_y^2}=1$; $\delta =\frac{\pi }{2}$为右旋，$\delta =-\frac{\pi }{2}$为左旋，为正椭圆偏振光
3. 一般情况

$$\frac{E_x^2}{A_x^2}+\frac{E_y^2}{A_y^2}-\frac{2E_x{E}_y}{A_x{A}_y}\cos \delta ={\sin }^2\delta$$

此时$-\pi <\delta <0$为左旋，$0<\delta <\pi$为右旋，为斜椭圆

自然光经过波晶片

• 自然光可正交分解，每一个分量都含有相位随机的多列波，在晶体中分为相互正交的o光、e光
• 经过波片后，每一个分量仍然是相位随机的多列波 . 所以，正交分量合成后，仍是自然光
• 不考虑波片的吸收，光强不变

线（平面）偏振光经波晶片

在波片中分为正交的e光、o光，它们在晶体内传播速度不同，穿过晶片时产生一定附加的相位$\delta$. 射出晶片后两光束的速度恢复到一样，合成在一起一般得到椭圆偏振光. 其中

$$\delta =\frac{2\pi }{\lambda }(n_o-n_e)d$$

要获得圆偏振光需要

1. $\delta =\pm \frac{\pi }{2}$，厚度满足这一点的波片被称为四分之一波片
2. $A_e=A_0$，设入射的线偏振光的振幅为$A$，其振动方向与e轴的夹角为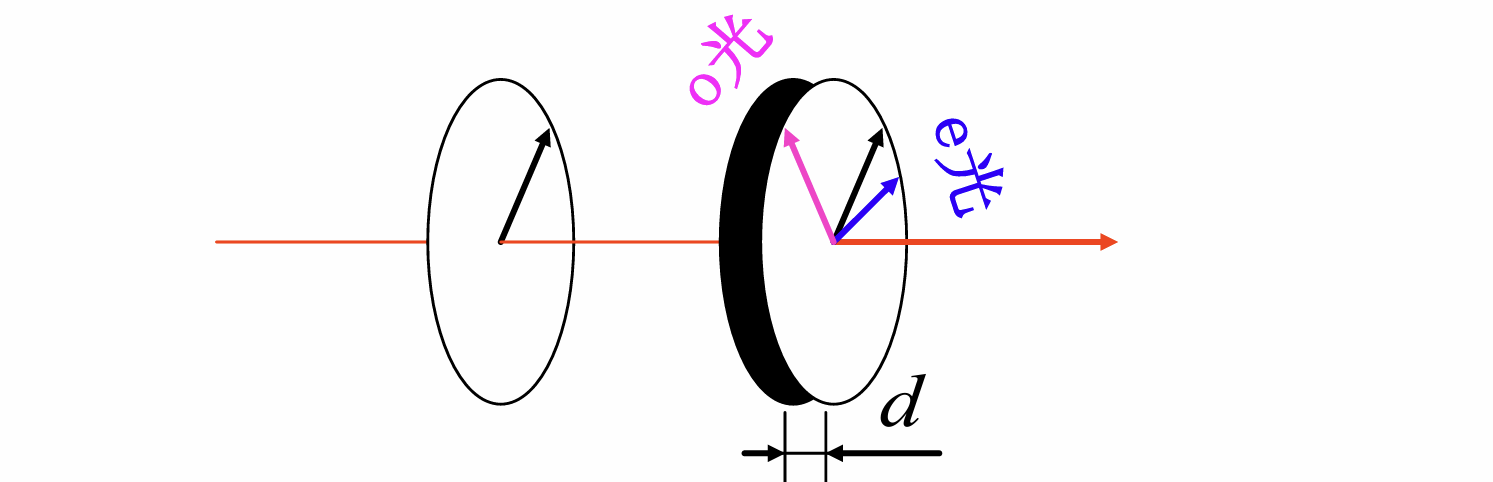$\alpha$，则必须有$\alpha =\frac{\pi }{4}$ 由此可以获得圆偏振光和椭圆偏振光

圆偏振光通过1/4波片

入射光的两正交分量间相位差为$\pm \frac{\pi }{2}$，经过1/4波片后产生$\pm \frac{\pi }{2}$的额外相位差，故出射光正交分量间的相位差是$0,\pi$，故变为线偏振光，电矢量和光轴成$45^{\circ }$角

椭圆偏振光通过1/4波片

斜椭圆偏振光通过后仍然是斜椭圆偏振光 正椭圆偏振光（椭圆长短轴和光轴重合），入射光的两正交分量间相位差为$\pm \frac{\pi }{2}$，故出射光也是线/平面偏振光

圆偏振光和椭圆偏振光的检验

1. 使用线验偏器

旋转检偏器，观察透射光强度的变化

• 自然光：光强不变
• 圆偏振光：光强不变
• 线偏振光：光强改变，在某一角度消光
• 部分偏振光：光强改变，但不消光
• 椭圆偏振光：光强改变，但不消光

2. 通过1/4波片

• 自然光：仍是自然光
• 圆偏振光：变为线偏振光
• 部分偏振光：仍是部分偏振光
• 椭圆偏振光：仍是椭圆偏振光，当光轴与椭圆长短轴重合，可以得到平面偏振光
• 再通过线检偏器，可以将自然光与圆偏振 光鉴别；部分偏振光与椭圆偏振光鉴别

旋光

如果将一束线偏振光射入石英片，那么出射的光也是线偏振光，但是其振动面向左或向右旋转了一个角度$\psi$，这种现象叫做旋光

实验表明，振动面旋转角度$\psi$与石英晶片的厚度$d$成正比

$$\psi =\alpha d$$

比例系数$\alpha$叫做石英的旋光率，旋光率的数值因波长而异，因此在白光照射下，不同颜色的振动面旋转的角度不同，所以在石英片后放上偏振片，将观察到色彩的变换，这种现象叫做旋光色散

石英晶体有左旋和右旋两种变体，它们的外形完全相似，只是一种是另一种的镜像反演，两种晶体使振动面的旋转方向相反

为了解释旋光性，Fresnel作出了如下假设：在旋光晶体中线偏振光沿光轴传播时分解为左旋和右旋圆偏振光（L光和R光），它们的传播速度$v_L,v_R$略有不同，或者说二者的折射率$n_L=\frac{c}{v_L},n_R=\frac{c}{v_R}$不同，从而经过旋光晶片时产生不同的相位滞后

$${\varphi }_L=k\Delta L_L=\frac{2\pi }{\lambda }{n}_{L}d,{\varphi }_R=k\Delta L_R=\frac{2\pi }{\lambda }{n}_{R}d$$

假设沿$x$方向振动的线偏振光可以分解为如下的左旋圆偏振光和右旋圆偏振光

$$L:\{\begin{array}{l}{E}_x=A\cos (\omega t)\\ E_y=A\cos (\omega t-\frac{\pi }{2})\end{array}R:\{\begin{array}{l}{E}_x=A\cos (\omega t)\\ E_y=A\cos (\omega t+\frac{\pi }{2})\end{array}$$

它们的合成是$E_x=2A\cos (\omega ),E_y=0$，而经过波片后有

$$L^{\prime }:\{\begin{array}{l}{E}_x=A\cos (\omega t+{\varphi }_L)\\ E_y=A\cos (\omega t-\frac{\pi }{2}+{\varphi }_L)\end{array}{R}^{\prime }:\{\begin{array}{l}{E}_x=A\cos (\omega t+{\varphi }_R)\\ E_y=A\cos (\omega t+\frac{\pi }{2}+{\varphi }_R)\end{array}$$

合成后变为

$$\{\begin{array}{l}{E}_x=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\cos \left(\frac{{\varphi }_L-{\varphi }_R}{2}\right)\\ E_y=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\cos \left(\frac{{\varphi }_L-{\varphi }_R-\pi }{2}\right)\end{array}$$

也就是

$$\{\begin{array}{l}{E}_x=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\cos \left(\frac{{\varphi }_L-{\varphi }_R}{2}\right)\\ E_y=2A\cos \left(\omega t+\frac{{\varphi }_L+{\varphi }_R}{2}\right)\sin \left(\frac{{\varphi }_L-{\varphi }_R}{2}\right)\end{array}$$

所以最后合成的线偏振光的方向和原来就偏离了一个角度

$$\psi =\frac{1}{2}({\varphi }_L-{\varphi }_R)=\frac{\pi }{\lambda }(n_L-n_R)d$$

因为把$x-y$坐标系逆时针旋转$\psi$角度后，就有$E_x=2A\left(\omega t+{\phi }_0\right),E_y=0$

光物质作用

光的吸收

光吸收的线性规律

令单色平行光束沿$x$方向通过均匀介质. 设光的强度在经过厚度为$\mathrm{d}x$的一层介质时强度由$I$减为$I-\mathrm{d}I$. 实验表明，在相当广阔的光强范围内，有

$$-\mathrm{d}I=\alpha I\mathrm{d}x$$

式中$\alpha$是一个与光强无关的比例系数，称为该物质的吸收系数

为了求出光束穿过厚度为$l$的介质后强度的改变，只需把上式改写为

$$\frac{\mathrm{d}I}{I}=-\alpha \mathrm{d}x$$

积分就有

$$\begin{array}{rl}\ln (\frac{I}{I_0})& =-\alpha l\\ ⟹I& =I_0{\mathrm{e}}^{-\alpha l}\end{array}\text{\hspace{1em}(1)}$$

式子中$I_0$和$I$分别代表$x=0,l$处的光强，$\alpha$的量纲是长度的倒数. 上式被称为Bouguer定律或者Lambert定律

线性吸收规律在激光发明之前是相当精确的，但是如果光强很强，光的非线性性质就会呈现出来，这个领域称为非线性光学

复数折射率的意义

透明介质折射率的本意是$n=\frac{c}{v}$，而在介质中沿$x$方向传播的平面电磁波中的电场强度可写作如下形式

$$\tilde{E}={\tilde{E}}_0\exp \left[-\mathrm{i}(\omega t-\frac{x}{v})\right]={\tilde{E}}_0\exp \left[-\mathrm{i}\omega (t-\frac{nx}{c})\right]$$

这里的$n$是实数，电磁波不随距离衰减. 如果我们形式地把折射率看作是复数，并且记作

$$\tilde{n}=n(1+\mathrm{i}\kappa )$$

其中$n$和$\kappa$都是实数，则上式化为

$$\tilde{E}={\tilde{E}}_0\exp \left[-\mathrm{i}\omega (t-\frac{\tilde{n}x}{c})\right]={\tilde{E}}_0\exp \left(-\frac{n\kappa \omega x}{c}\right)\exp \left[-\mathrm{i}\omega (t-\frac{nx}{c})\right]\text{\hspace{1em}(2)}$$

而光强为

$$I\propto {\tilde{E}}^{\ast }\tilde{E}=\left|E_0\right|\exp \left(\frac{2n\kappa \omega x}{c}\right)$$

故这个式子表示一个随距离$x$衰减的平面波，故称$\kappa$为衰减系数. 比较$(2)$式和$(1)$式就有

$$\alpha =\frac{2n\kappa \omega }{c}=\frac{4\pi n\kappa }{\lambda }$$

光的吸收和波长的关系

若物质对各种波长$\lambda$的吸收程度几乎相等，即吸收系数$\alpha$和$\lambda$无关，则称为普遍吸收. 在可见光的范围内的普遍吸收意味着光束通过介质后只改变强度，不改变颜色. 例如空气、纯水，无色玻璃等介质都在可见光范围内产生普遍吸收

若物质对某些波长的光的吸收特别强烈，则成为选择吸收，对可见光进行选择吸收，会使白光变成彩色光. 绝大部分物体呈现彩色，都是其表面活体内对可见光进行选择吸收的结果

对于广谱的电磁波而言，不存在普遍吸收的物质，实际上选择吸收才是物质和光相互作用的普遍规律

吸收光谱

令具有连续谱的光（白光）通过吸收物质后再经过光谱仪分析，可形成吸收光谱. 对于同一物质而言，其发射光谱中的亮线和吸收光谱中的暗线是一一对应的，也就是说，某种物质自身发射哪些波长的光，他就强烈地吸收哪些波长的光

太阳的吸收光谱中的暗线被称为Fraunhofer谱线，用字母$\mathrm{A},\mathrm{B},\mathrm{C},\cdots$表示. 把这些吸收谱线的波长和地球上已知物质发射原子光谱对比以下，就可以知道太阳表面层中包含哪些元素

光的色散

正常色散

光在介质中的传播速度$v$(或者说折射率$n=\frac{c}{v}$)随波长$\lambda$而异的现象称为色散

回忆三棱镜的色散作用，测量不同波长的光通过棱镜的偏转角，就可以算出棱镜材料的折射率$n$与波长$\lambda$之间的依赖关系曲线，即色散曲线. 实验表明，凡是在可见光范围内无色透明的介质，它们的色散曲线在形式上很相似，比如说$n$随着$\lambda$的增加而单调下降，且下降率在短波一端更大. 这种色散被称为正常色散 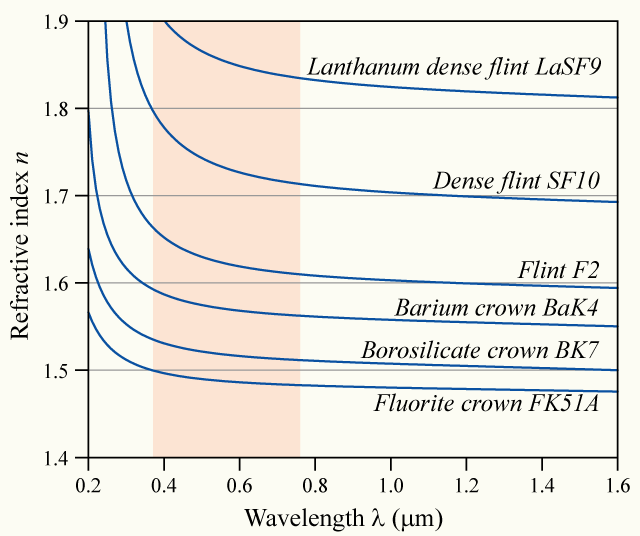1836年Cauchy给出了一个正常色散的经验公式

$$n=A+\frac{B}{{\lambda }^2}+\frac{C}{{\lambda }^4}$$

当$\lambda$变化范围不大时，可以只取前两项

$$n=A+\frac{B}{{\lambda }^2}$$

反常色散

实验表明，在强烈吸收的波段，色散曲线与正常色散曲线有很大的不同. Wood在观察钠蒸汽的色散的时候，发现在钠的吸收线附近，水平光谱段被严重的扭曲和割断，这种现象叫做反常色散 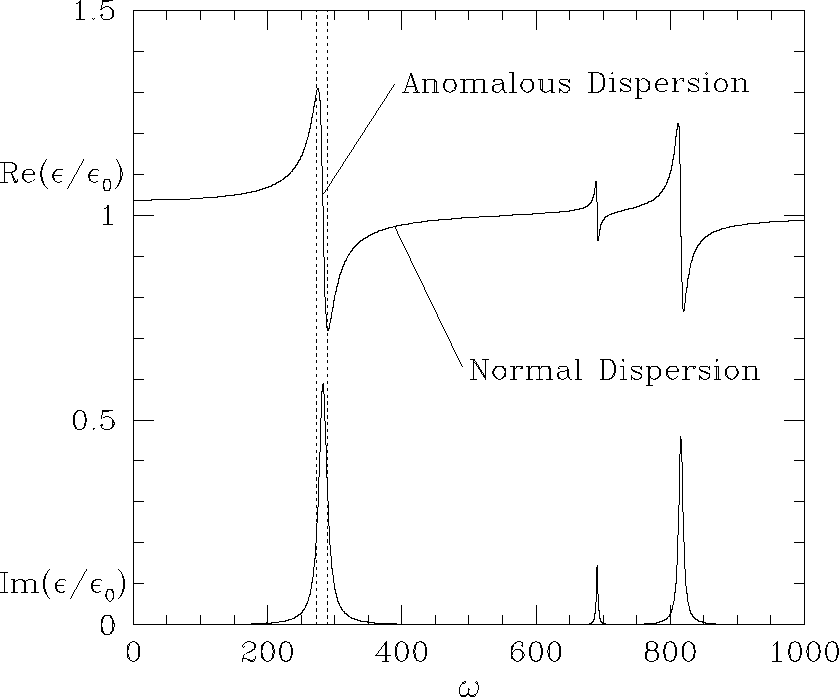反常色散的名称时历史上沿用下来的，其实任何物质在吸收线附近都有反常色散的现象，所以这种现象严格意义上不能算作“反常”

一种物质的全部色散曲线

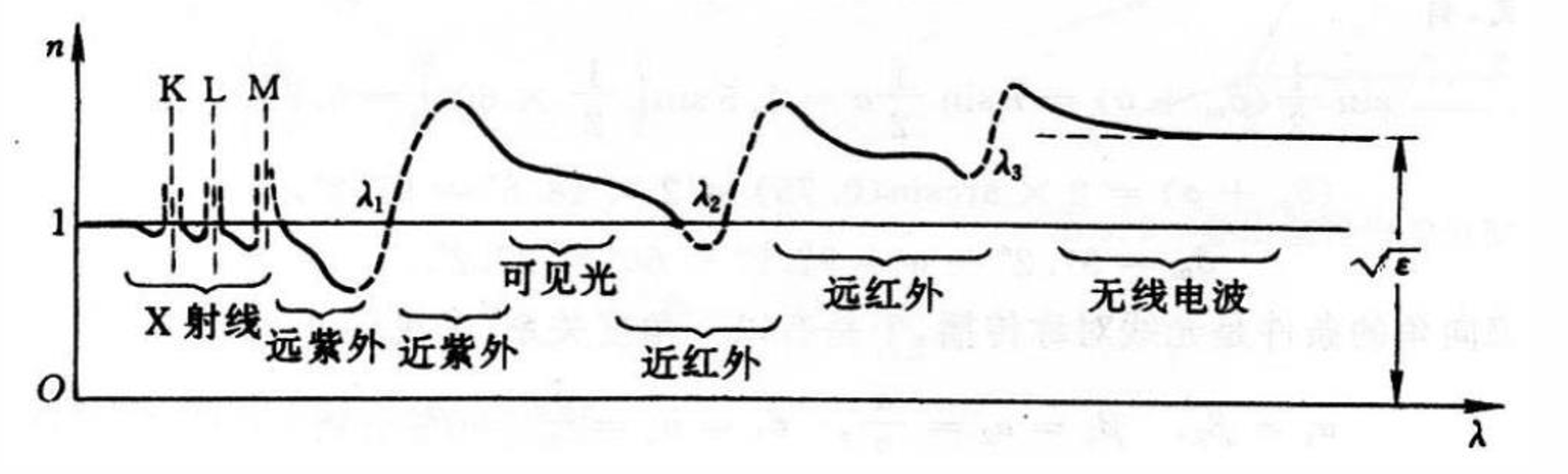在相邻的两个吸收带之间$n$随着$\lambda$单调下降，每次经过一个吸收带，$n$急剧增大. 总的趋势是曲线随着$\lambda$的增加而抬高

群速和相速

一般而言，当我们提及光在各向同性介质中的波速时，都指的是波面（等相位面）传播的速度，即相速（phase velocity），用$v_p$来表示. 在真空中所有波长的电磁波以同一相速$c$传播，在色散介质中只有理想的单色波具有单一的相速.

但是理想的单色波是不存在的，波列不会无限长. 一列有限长的波相当于许多单色波列的叠加，通常把由这样一群单色波组成的波列叫做波包（wave packet）. 当波包通过有色散的介质时，它的各个单色分量将以不同的相速前进，整个波包在向前传播的同时，其形状也会发生变化. 称波包中振幅最大的地方叫做它的中心，以波包中心为代表的前进速度叫做群速（group velocity）

在介质中，$f$不变，而$\lambda =\frac{c}{nf}$，设$\omega =2\pi f,k=\frac{2\pi }{\lambda }=\frac{2\pi nf}{c}$，我们有$v_p=\frac{c}{n}=\frac{\omega }{k}$，而通过Fourier变换，可以推导得

$$v_g=\frac{\mathrm{d}\omega }{\mathrm{d}k}$$

注意到$n=\frac{c}{v_p}=\frac{ck}{\omega }$，于是

$$\frac{\mathrm{d}n}{\mathrm{d}\omega }=\frac{c}{\omega }\frac{\mathrm{d}k}{\mathrm{d}\omega }-\frac{ck}{{\omega }^2}$$

也就是

$$\omega \frac{\mathrm{d}n}{\mathrm{d}\omega }=\frac{c}{v_g}-\frac{c}{v_p}$$

定义折射率$n=\frac{c}{v_p}$，群速折射率$n_g=\frac{c}{v_g}$，则有

$$\boxed{n_g=n-\lambda \frac{\mathrm{d}n}{\mathrm{d}\lambda }}$$

上式也说明了没有色散（$\frac{\mathrm{d}n}{\mathrm{d}\lambda }=0$）时，群速和相速没有区别.

除了根据用Huggens原理直接用折射率法测出得光在介质中得速度时相速度之外，大多数其他方法测出得其实是光的信号速度，也就是能量的传播速度. 而波包中振幅最大的地方也就是能量最集中的地方，所以可以认为我们一般测到的光速都是群速度

有些时候，相速度$v_p$是可以超过光速$c$的，但是波的信号速度总是小于$c$. 在正常色散区，波的信号速度就是其群速度，它总是小于$c$的；但是在反常色散区，群速度可以大于$c$，也可以是负值，但是这个时候群速度显然就不能代表信号速度了，实验证明，光传播信号的速度确无法大于光速$c$

色散本领

回忆光栅的色分辨原理

光的散射

散射与介质不均匀尺度之间的关系

光线在通过均匀的透明介质时，从侧面是难以看到光线的. 如果介质不均匀，如有悬浮微粒的浑浊液体，我们可以从侧面清晰地看到光线的轨迹. 这是介质中的不均匀性使得光线朝四面八方散射的结果

Rayleigh散射

Rayleigh认为散射光强和波长的四次方成反比，即

$$I\propto \frac{1}{{\lambda }^4}$$

这个理论可以解释很多的自然现象

如白昼天空之所以是亮的，完全是大气散射阳光的结果. 如果没有大气，即使在白昼，天空除了太阳本身也将是漆黑的. 按照Rayleigh定律，白光中的短波成分（蓝紫色）遭到的散射比长波成分（红黄色）强烈得多，散射光因短波的富集而显蔚蓝色. 而在大雨初霁时，大气的密度涨落程度更高，散射作用更强，所以天空将更蓝

旭日和夕阳呈红色，是因为白光中的短波成分更多的被散射掉了，在直射的日光红较多的自然是长波成分. 而早晚阳光以很大的倾角穿过大气层，经历的大气厚度要比中午时大很多，从而大气的散射效应也要强得多，所以这时候太阳呈现红色

散射的角度分布和偏振

如果入射光是线偏振的，那么散射光也是线偏振的 如果入射光是自然光，那么在垂直于入射光的方向上，散射光是线偏振的；在原入射方向或者其逆方向上，散射光是自然光，且前者的强度正好是后者的一半；在其他方向上，散射光是部分偏振的，强度介于前两个极端之间

Raman散射

Rayleigh散射不改变原入射光的频率，而Raman发现了在散射光中除了与入射光的原有频率${\omega }_0$相同的Rayleigh散射线外，谱线两侧还有频率为${\omega }_0\pm {\omega }_1,{\omega }_0\pm {\omega }_2,\dots$等散射线存在，这种现象被称为Raman散射

我们称长波一侧的散射线（${\omega }_0-{\omega }_j$）为红伴线或者Stokes线，在长波一侧（${\omega }_0+{\omega }_j$）的为紫伴线或者反Stokes线. 其中频率差${\omega }_j$和入射光的频率${\omega }_0$无关，而与散射物质的红外吸收频率相对应，表征了散射物质的分子振动频率

量子光学

黑体辐射

Stefan-Boltzmann定律

黑体的辐射本领和温度的四次方成正比

$$R=\sigma T^4,\sigma =5.67\times 10^{-8}\mathrm{W}\cdot {\mathrm{m}}^{-2}\cdot {\mathrm{K}}^{-4}$$

Wein位移定律

黑体辐射中最强辐射的波长和温度成反比

$${\lambda }_{m}T=b,b=2898\mu \mathrm{m}\cdot \mathrm{K}$$

Planck黑体辐射定律

在任意温度$T$下，从一个黑体中发射出的电磁辐射的辐射率是频率$\nu$的函数

$$L_{\nu }(\nu ,T)=\frac{2h{\nu }^3}{c^2}\frac{1}{\exp (\frac{h\nu }{k_{B}T})-1}$$

其中$L_{\nu }$是光谱辐射率，$k_B$是Boltzmann常数，或者写成波长的函数

$$L_{\lambda }(\lambda ,T)=\frac{2h{c}^2}{{\lambda }^5}\frac{1}{\exp (\frac{hc}{\lambda k_{B}T})-1}$$

注意这两个函数具有不同的单位：第一个函数是描述单位频率间隔内的辐射率，而第二个则是单位波长间隔内的辐射率. 因而它们不等价且有如下关系

$$I_{\nu }(\nu ,T)\mathrm{d}\nu =-I_{\lambda }(\lambda ,T)\mathrm{d}\lambda$$

通过单位频率间隔和单位波长间隔之间的关系，这两个函数可以相互转换

$$\mathrm{d}\nu =\mathrm{d}\left(\frac{c}{\lambda }\right)=c\mathrm{d}(\frac{1}{\lambda })=-\frac{c}{{\lambda }^2}\mathrm{d}\lambda$$

光电效应

逸出功与极限频率${\nu }_0$之间的关系为

$$W_0=h{\nu }_0$$

克服逸出功之后，光电子的最大动能$E_{\max }$为

$$E_{\max }=h\nu -W_0=h(\nu -{\nu }_0)$$

激光的基本概念

激光（Laser），或者写为LASER，是Light Amplification by Stimulated Emission of Radiation的缩写，中文意思为受激辐射的光放大

正常情况下，大多数粒子处于基态，要使这些粒子产生辐射作用，必须把处于基态的粒子激发到高能级上去. 由于原子内部结构不同，相同的外界条件使原子从基态激发到各高能级的概率不同. 通常把原子、分子或离子激发到某一能级上的可能性称为这一能级的激发概率

理论研究表明，光的发射过程分为两种，一种是在没有外来光子的情况下，处于高能级$E_2$的一个原子自发地向低能级$E_1$跃迁，并发射一个能量为$E_2-E_1$的光子，这种过程称为自发跃迁；由原子自发跃迁发出的光波称为自发辐射

另一种发射过程是处于高能级$E_2$上的原子，在频率为$\nu$的辐射场作用下，跃迁至低能级$E_1$并辐射一个能量为$E_2-E_1=h\nu$，与激励光子完全相同的光子，这种过程称为受激发射跃迁；受激发射跃迁发出的光波，称为受激辐射

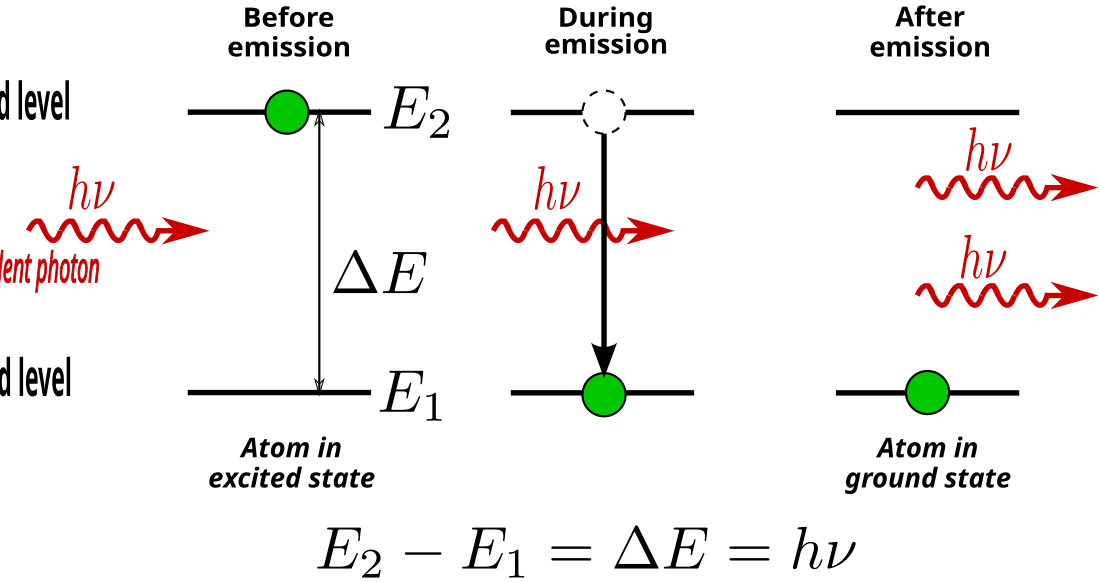
受激辐射与自发辐射最重要的区别在于干涉性. 自发辐射是原子在不受外界辐射场控制情况下的自发过程，大量原子的自发辐射场的相位是不干涉的，辐射场的传播方向和偏振态也是无规分布，而受激辐射是在外界辐射场控制下的发光过程. 因此，受激辐射场的频率、相位、传播方向和偏振态与外界辐射场完全相同. 激光就是一种受激辐射的干涉光.