几何光学基础
折射率定义
变折射率问题
光线方程
棱镜
最小偏向角满足
此时光线对称入射出射
霓虹
- 光线路径不同:
- 虹是由太阳光进入水滴后经过一次折射和一次反射而形成的.
- 而霓是由太阳光进入水滴后经过两次折射和两次反射而形成的.
- 颜色排列不同:
- 虹内紫外红
- 霓内红外紫
- 亮度差异:
- 虹的亮度较强,颜色鲜艳.
- 而霓的亮度较弱,颜色较为暗淡
晕
六角柱状冰晶横躺着缓慢下降, 光在冰晶中的折射最小偏向角为22°左右 六角柱体状冰晶竖着缓慢下降, 则阳光折射的最小偏向角为46°左右
成像
光具组把以物点为中心的同心光束转变为以像点为中心的同心光束
像的分类
实像: 出射光束是会聚的 虚像: 出射光束是发散的 实物: 入射光束是发散的 虚物: 入射光束是会聚的
物方和像方
- 物方: 物点所处的空间, 又称物空间, 包括所有实的和虚的物点, 是所有物点的集合, 因而不仅包括光具组前方的空间(实物), 还包括光具组后方的空间(虚物)
- 像方: 像点所处的空间, 又称像空间, 包括所有实的和虚的像点, 是所有像点的集合, 因而不仅包括光具组后方的空间(实像), 还包括光具组前方的空间(虚像)
等光程性
物象之间所有光线等光程
严格成像
严格保持同心性
理想光具组
任意点严格成像
等光程面
反射(三种)
折射(一种, 和特殊例子)
共轴球面组傍轴成像
共轴球面光具组
球心在一条直线
成像公式 和 符号规定
折射
反射
焦点定义
物方
像方
焦距
在
中代入或 有
光焦度
一个球面光具有两个焦距, 但是只有一个光焦度
横向放大率
折射
反射
拉格朗日—亥姆霍兹不变量
薄透镜
焦距公式
其中
磨镜者公式
如果则有
光焦度
就是眼睛的度数
密接透镜组
作图法
要点是焦面上的每一个点发出的光线通过透镜后都会变平行
逐次成像
理想光具组
定义
- 同心光束的不变性. 光具组中各个光束保持同心性
- 物像间的相似性. 空间上各个点之间的相互位置要一一对应, 同时每一对物像点的颜色也要一一对应
- 没有像差和色差等. 理想光具组不会产生畸变、像差或色差
主点和主面
主点(principle point) 和 主面(principle plane): 横向放大率等于的一对共轭面. 属于物方的为物方主面, 记作, 其与主轴交点称为物方主点, 记作, 属于像方的为像方主面, 记作, 其与主轴交点称为像方主点, 记作
光学仪器
眼睛
明视距离
近视 远视
近视用凹透镜矫正;远视用凸透镜
盲斑 黄斑
因为头、眼会转, 平时感觉不到盲斑的存在
视杆细胞
- 对于微弱光线非常敏感,主要负责暗视觉
- 富集于视网膜的周边区域
- 只能感知明暗,不能分辨颜色
- 在低照度条件下起主导作用
视锥细胞
- 对颜色和细节高度敏感,主要负责日间视觉
- 富集于视网膜中央区域,特别是黄斑中心凹
- 分为3种类型,分别对红、绿、蓝光敏感,共同编码色彩信息
- 在正常白天光照条件下起主导作用
视觉敏感度
对的绿光最敏感 色盲: 某类视锥细胞缺失 色弱: 视觉细胞并未缺失, 但响应能力较弱
其他动物
食肉动物
长在面部前方, 有较大的双眼交叠视觉, 有利于形成立体视觉来有效判断猎物的距离
食草动物
食草动物的眼睛一般长在头部两侧, 有更大的视觉范围, 有利于更早地发现天敌. 大部分食草动物对于颜色的分辨能力较弱.
鸟类
鸟类的眼睛与体型之比是所有动物最大的. 相比哺乳动物, 鸟类的睫状肌能更快地调节晶状体, 调节的范围也更大. (因为视距范围更广)
复眼
复眼由多个单元组成, 单个单元无法成像. 复眼提供了很大的视觉范围, 其空间分辨率低于人眼, 但其时间分辨率(动态分辨率)高于人眼约倍
放大镜和目镜
放大镜的作用是放大视角, 而非放大实际大小 在没有放大镜的时候, 由于明视距离的存在, 高度为的物体所能呈现的最大视角就是
现在我们有一个放大镜, 需要把物体放大成虚像(一倍焦距之内), 且像不能进入人的明视距离之内, 所以需要把物放在焦点内侧很小的距离之内, 由几何上的相似三角形, 像的视角就是物的视角
于是有角放大率
显微镜和望远镜中的目镜本质上也是放大镜
显微镜
- 物镜把物放大成一个倒立的实像
- 目镜再把这个倒立实像放大成更大的虚像
被观察的物体放在物方焦点外侧附近, 它经过物镜放大成像至目镜物方焦点内侧附近, 再经目镜放大称虚像于明视距离以外
因为第一次放大物里物方焦点足够近, 所以像离像方焦点足够远, 而目镜又必须要比像里物镜更远, 所以物镜和目镜之间的距离远大于它们的焦距
显微镜的总放大率为物镜横向放大率和目镜角放大率 的乘积
其中是物镜像方焦点到目镜物方焦点的距离, 被称为光学筒长
望远镜
原理和显微镜类似, 区别在于
- 物在无穷远处, 故物镜的像成在其像方焦面上
- 物镜的像方焦点和目镜的物方焦点几乎重合 定义其视角放大率为最后的虚像对目镜所张视角 和物体在实际位置所张视角之比
上述是开普勒式, 对于伽利略式有
照相机
镜头和焦距: 相机镜头收集光线并将其聚焦到图像传感器或胶片上. 镜头的焦距决定了视角和放大倍率 - 较短的焦距提供更宽的视角, 而较长的焦距提供更大的变焦和放大倍率
光圈(光阑): 镜头中的光圈或光圈控制进入相机的光量. 较宽的光圈(较小的 f 值)允许更多的光线但较浅的景深 , 而较窄的光圈(较大的 f 值)会减少光线但增加景深.
投影仪
把物方焦点附近的物投影到屏上, 因而放大率
应用光学
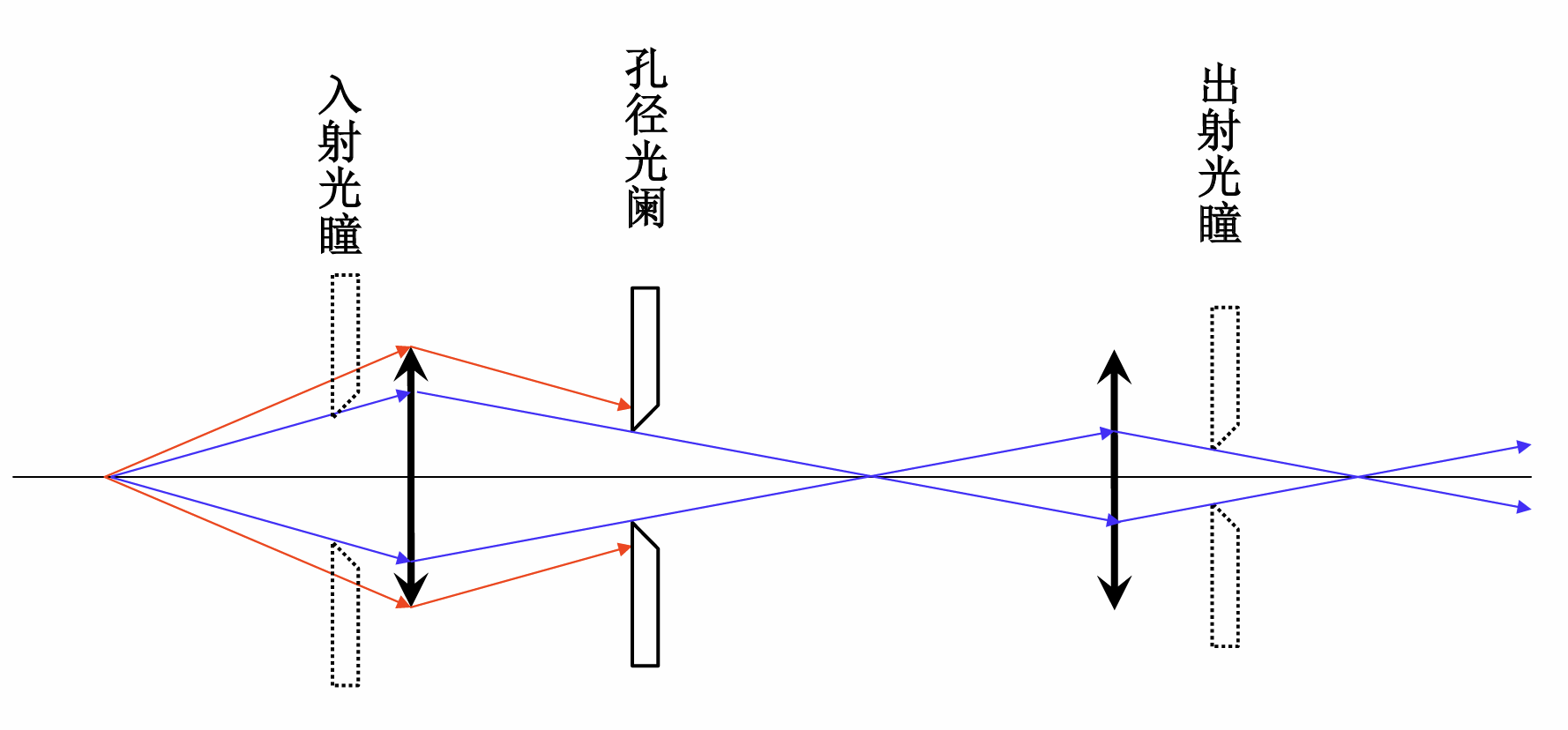
光阑
对光具组成像时的光束孔径、成像点偏离光轴的范围加以限制的透镜边框、框架或特别设置的带孔屏障 光阑是球面光具组近似成像的必然要求
孔径光阑
决定轴上物点通过光具组光束孔径的光阑称为孔径光阑或有效光阑. 被孔径光阑所限制的物、像方成像光束的张角分别叫做入射孔径角和出射孔径角 孔径光阑是轴上物点傍轴条件的要求
入射光瞳和出射光瞳
孔径光阑在物方和像方的共轭
视场光阑
决定轴外物点的主光线能否通过光具组的光阑. 恰好能通过光具组主光线与光轴在物方和像方的夹角叫做入射视场角和出射视场角
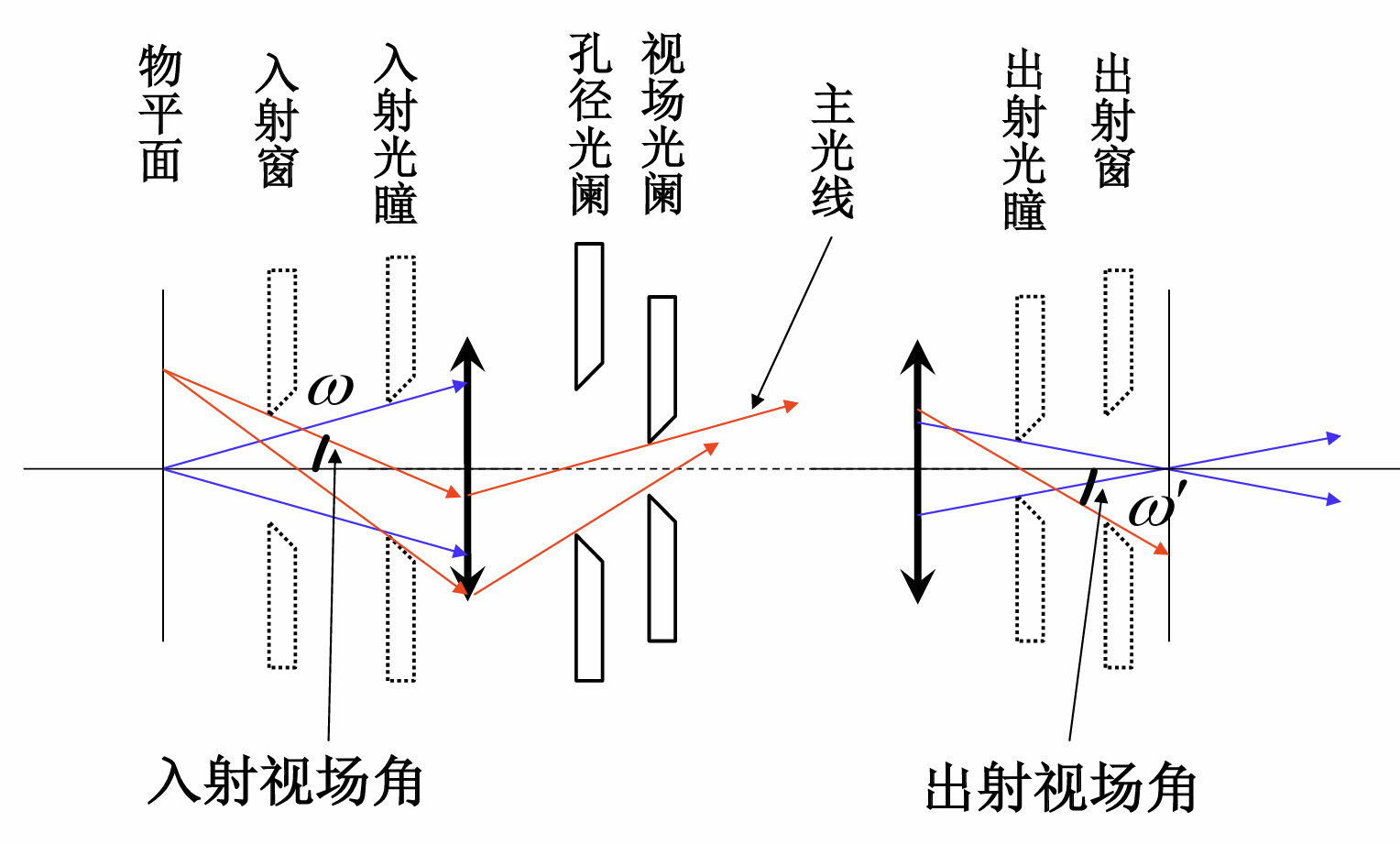 视场光阑是轴外物点傍轴条件的要求
视场光阑是轴外物点傍轴条件的要求
入射窗和出射窗
视场光阑在物方和像方的共轭
渐晕
当物点逐渐远离光轴时, 参与成像的光线逐渐减少, 导致图像逐渐昏暗, 称作渐晕. 当入射窗就在物平面上时, 渐晕将不出现.
所以在设计入射窗和入射光瞳的时候, 要尽可能让光轴上的和偏离光轴上的物点能有相同的入射视场角, 这样才能使得每一个点的清晰度都相似
像差
球差
是指发生在经过透镜折射或面镜反射的光线, 接近中心与靠近边缘的光线不能将影像聚集在一个点上的现象. 这在望远镜和其他的光学仪器上都是一个缺点. 这是因为透镜和面镜必须满足所需的形状, 否则不能聚焦在一个点上造成的.
慧差
彗形像差是抛物镜望远镜与生俱来的特质, 来自于视野中心区域的点光源(像是恒星)可以很好的汇聚在面镜的焦点上(不同于球面镜, 来自于镜子周围部分的光线只是接近焦点—球面像差. ). 但是, 来自于偏离光轴(离轴)方向的光线, 自镜子的不同区域反射的光却不能汇聚在相同的焦点上. 这样的结果导致不在视野中心的光看起来是楔形的问题, 而且离轴越远, 这个现象越明显. 这使得星点看起来有着彗星的形状, 因而得名.
像散
具有像散的光学系统是指在两个垂直平面中传播的光线具有不同焦点的光学系统. 如果使用具有像散的光学系统来形成十字图像, 则垂直线和水平线将在两个不同距离处清晰聚焦.
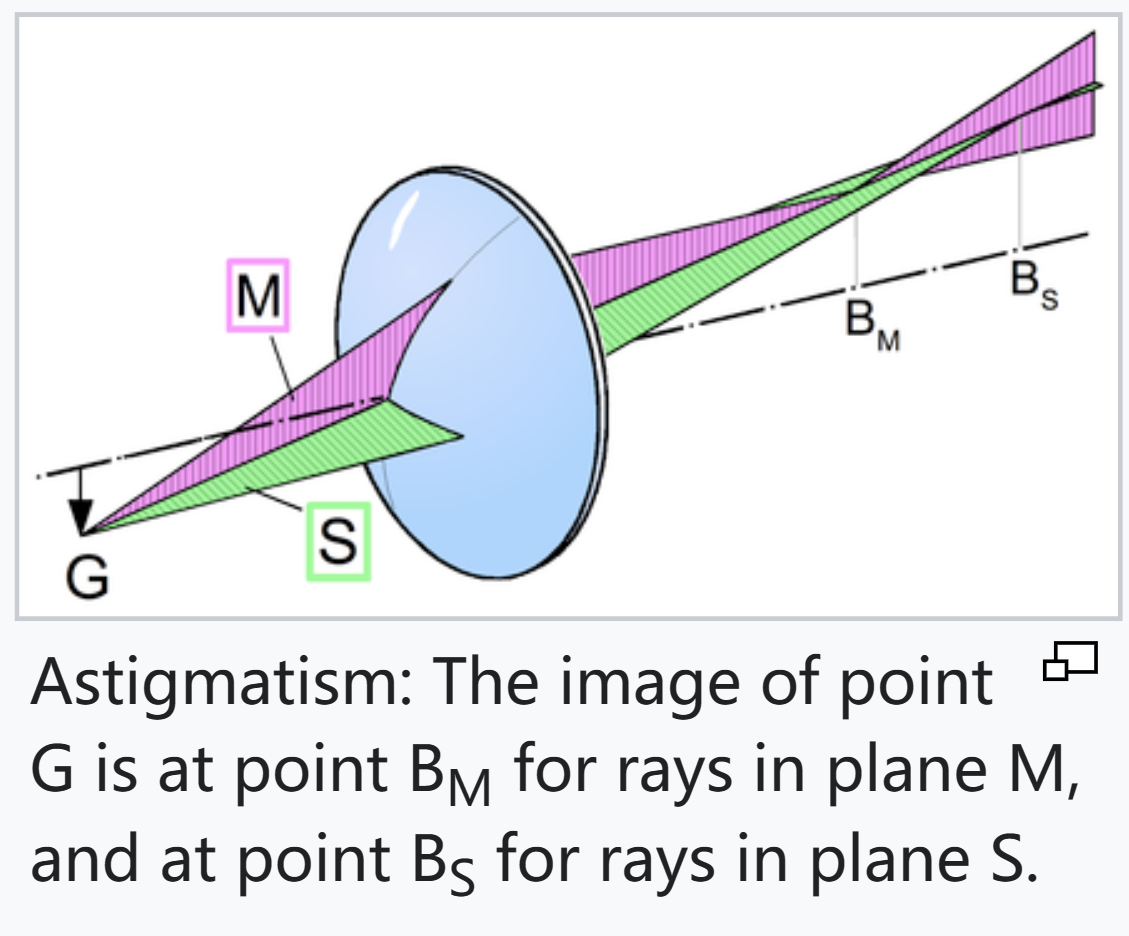 在验光和眼科中, 垂直和水平面分别被识别为切向子午线和矢状子午线. 眼科散光是一种眼睛的屈光不正, 其中不同经络的屈光度数存在差异
在验光和眼科中, 垂直和水平面分别被识别为切向子午线和矢状子午线. 眼科散光是一种眼睛的屈光不正, 其中不同经络的屈光度数存在差异
像场弯曲
是因镜片缺陷, 使垂直于主光轴的物平面上发出的光经透镜成像后, 清晰的最佳实像面不是平面而是一个曲面的一种像差. 1839年匈牙利物理学家约瑟夫·佩兹瓦尔最先从物理学角度阐明像场弯曲的原理, 为纪念他, 像场弯曲也称为佩兹瓦尔像场弯曲.
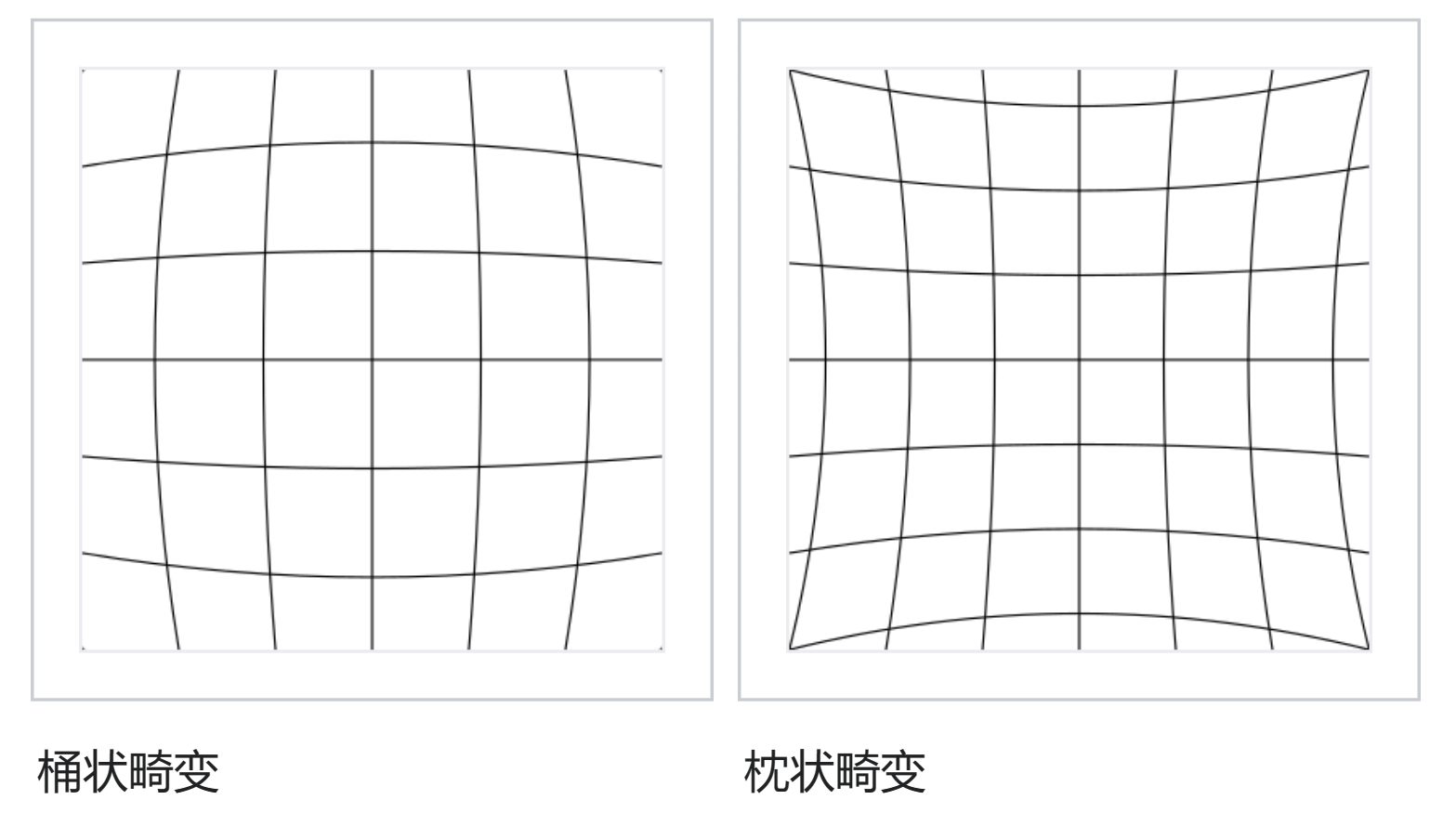
畸变
不影响镜头成像精细度. 畸变与物像点离光轴的垂直高度的立方成正比, 因此, 物像四角的畸变比物像的四边的畸变程度大
色差
色散(Chromatic Aberration, CA) 是指光学上透镜无法将各种波长的色光都聚焦在同一点上的现象. 它的产生是因为透镜对不同波长的色光有不同的折射率(色散现象). 对于波长较长的色光, 透镜的折射率较低. 在成像上, 色散表现为高光区与低光区交界上呈现出带有颜色的"边缘", 这是由于透镜的焦距与折射率有关, 从而光谱上的每一种颜色无法聚焦在光轴上的同一点. 色散可以是纵向的, 由于不同波长的色光的焦距各不相同, 从而它们各自聚焦在距离透镜远近不同的点上;色散也可以是横向或平行排列的, 由于透镜的放大倍数也与折射率有关, 此时它们会各自聚焦在焦平面上不同的位置
Abbe 正弦条件
对轴上物点大孔径成像
在光学中, Abbe 正弦条件是透镜或其他光学系统必须满足的条件, 才能产生离轴和同轴物体的清晰图像, 该条件要求物空间角的正弦值应该和像空间角的正弦值成正比, 且该比例应当等于系统的放大倍数
对于球面镜而言, 齐明点是一对满足Abbe 正弦条件的共轭点
光度学
辐射能通量和光通量
- 光度学 - 人眼(主观)
- 辐射度学 - 功率(物理) 定义光通量
其中是辐射能谱密度, 表示人眼对光波的敏感性, 的单位是流明
对于一个点光源, 这表示通过包含它的一个闭合曲面上的光能(按照人眼敏感度加权)的总和
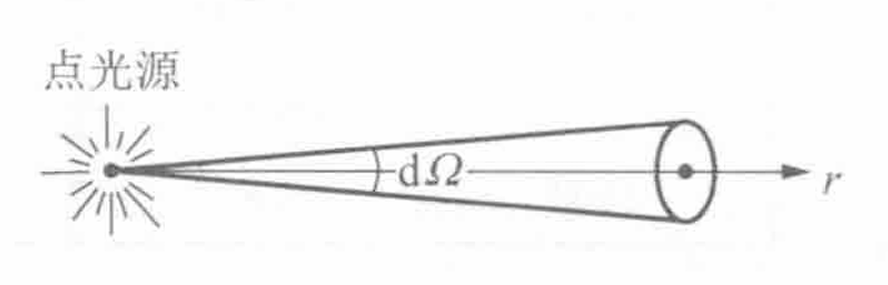
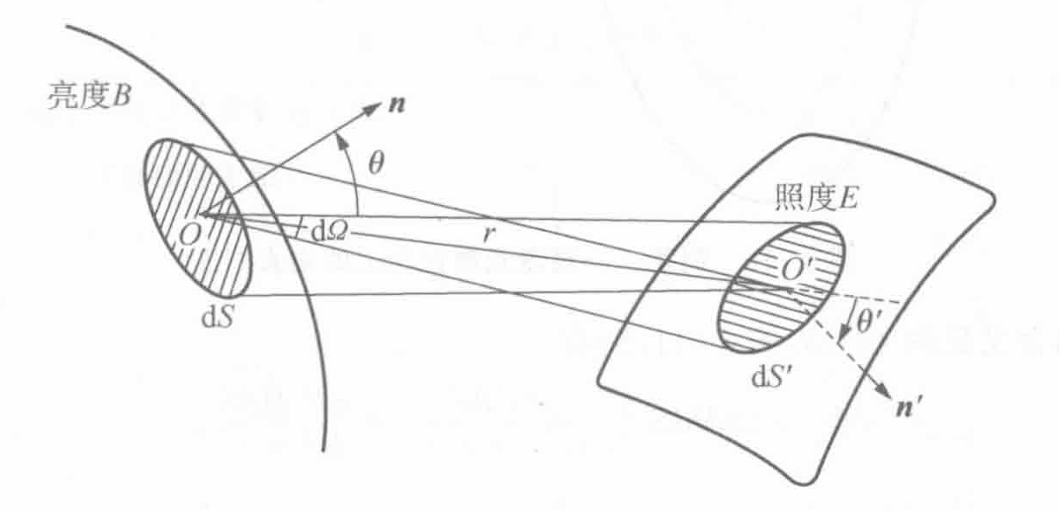
发光强度
当光源的线度足够小, 或距离足够远, 从而眼晴无法分辨其形状时, 我们把它叫做点光源. 在实际中多数情形里, 我们看到的光源有一定的发光面积, 这种光源叫做面光源, 或扩展光源
点光源沿某一方向的发光强度定义为沿此方向上单位立体角内发出的光通量. 我们以为轴取一立体角元, 设内的光通量为, 则沿方向的发光强度为
单位是, 坎德拉
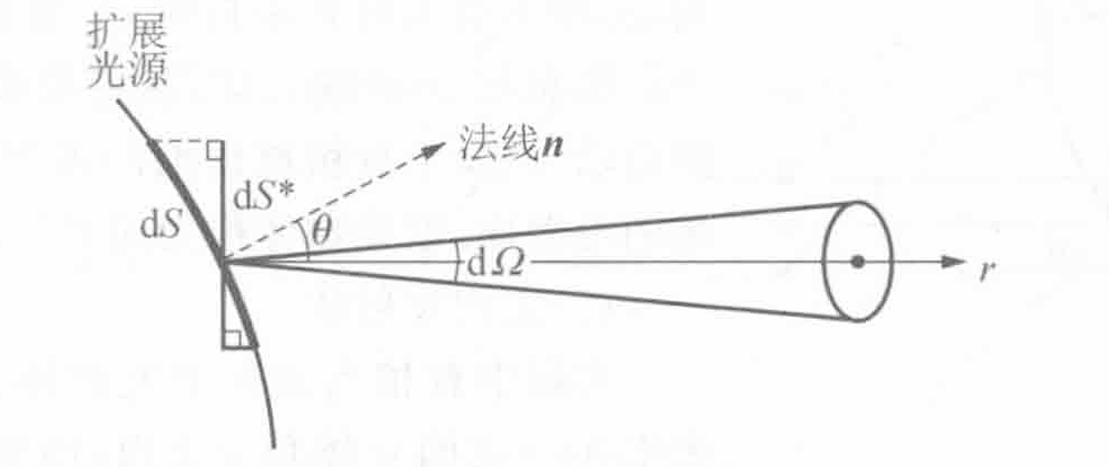
亮度
扩展光源表面的每块面元沿桌方向有一定的发光强度. 当一个观察者迎着的方向观察时, 它的投影面积为. 面元沿方向的光度学亮度(简称亮度)定义为在此方向上单位投影面积的发光强度
单位为, 熙提
 由Lagrange - Helmholtz 不变量 可知亮度是几何光学中的不变量
人眼对光线强度的感知主要来自于亮度, 而不是总的光通量
由Lagrange - Helmholtz 不变量 可知亮度是几何光学中的不变量
人眼对光线强度的感知主要来自于亮度, 而不是总的光通量
余弦发射体
又称为漫射体, Lambert 发光体, 其发光强度满足Lambert 定律
即从理想的漫反射表面或理想的漫反射体观察到的辐射强度或发光强度与观察者的视线与表面法线之间的夹角θ的余弦成正比
一个均匀的球形余弦发射体, 从远处的观察者看来, 与同样半径同样亮度的一个均匀发光圆盘无异. 因为我们可以把面对观察者的半球上每个面元投影到圆盘上, 得到一个面积为的面元. 这两个面元在指向观察者方上的发光强度和投影面积都是一样的, 因而亮度也一样
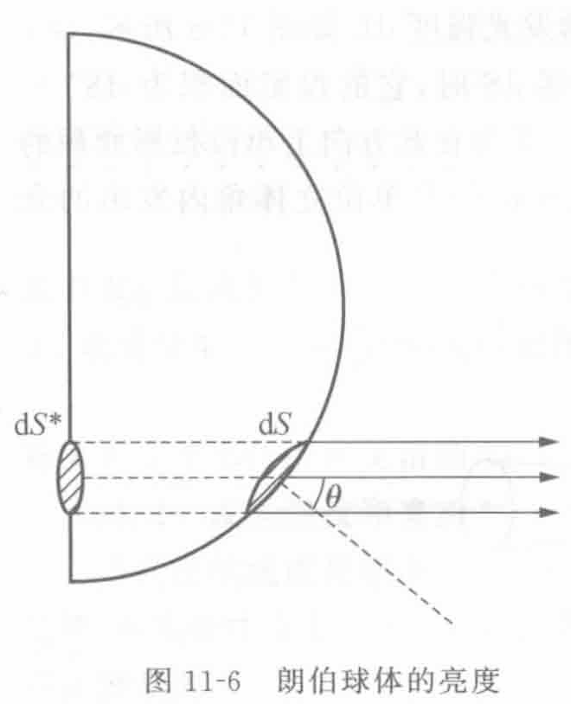
太阳看起来近似像一个亮度均匀的圆盘, 这表明它接近于一个余弦发射体此外, 日常生活里常见的光源, 许多接现实中大部分的发光体都是余弦发光体
照度
照度(illuminance) 是每单位面积所接收到的光通量;可理解为: 单位面积内获得多少光
单位是, 勒克斯
点光源照度
对于发光强度为的点光源, 其产生的光通量和照度
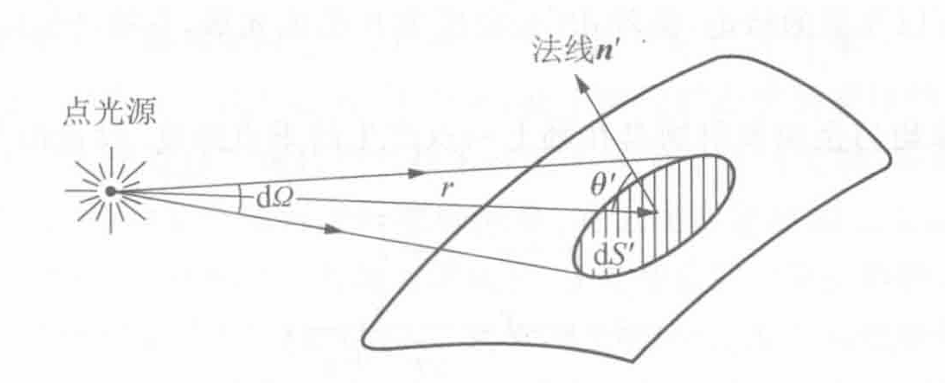
面光源照度
在光源表面和被照表面各取一个面元和, 令二者连线和各自法线的夹角未, 面光源的亮度为, 则由发出并照射在上的光通量是
于是有
总结
- 光通量: 实际计算中的中间转化量
- 发光强度: 描述光源的性质, 只和光源本身有关, 单位立体角内的光通量
- 亮度: 描述光源, 但是和观察角度和距离有关, 单位投影面积上的发光强度
- 照度: 描述被照射面, 单位面积上接受到的光通量
电磁原理
定态光波
定态波场
- 空间各点的扰动是同频率的简谐振动
- 波场中各点扰动的振幅不随时间变化, 扰动在空间形成一个稳定的振幅分布
- 光波的传播方程
符合定态波场的条件
复振幅描述
其中为场点, 是振幅的空间分布, 是相位的空间分布. 上式可用复数表示为
并写成时空分离的形式
其中为复振幅, 同时包含了定态波场中的振幅空间分布和相位的的空间分布
可以把上述表示法拓展到 平面波
题目常出在Descartes坐标系中, 对于一束光波, 是不变的, 具体的要扫描出待分析的波前. 具体计算时, 对于汇聚光线指向源点;对于发散光线, 以源点为起点. 总是以源点为起点的 球面波
注意振幅是一次反比而不是平方反比
波强度
波前
概念
波场中任一曲面, 更多地是指一个平面
复振幅互为复数共轭的波, 称为共轭波
傍轴条件和远场条件
对于一个点光源, 它发出的球面波在很小的横向线度内和很大的距离外可以被看做平面波
傍轴条件
保证波前上接收到的振幅分布和平面波一样和场点无关
远场条件
保证波前上接收到的相位分布也具有平面波的特点
上面的定义为接受平面上场点到轴的距离
在光学中往往是远场条件比傍轴条件更强
于是, 在满足傍轴条件时, 有
同时满足傍轴条件和远场条件时
偏振
光的横波性
声波是纵波、疏密波, 不存在偏振现象 光波是横波, 偏振是横波特有的性质, 所以可以利用偏振片验证横波
偏振片
只让某一振动方向光波通过的光学元件称为偏振片. 这个方向被称为偏振片的透振方向或偏振方向
偏振片按其用途(获得偏振光、检验偏振光)分别称为起偏器、检偏器
立体电影
在观看立体电影时, 观众需要戴上一副眼镜, 这就是一对透振方向互相垂直的偏振片. 其原理是平时我们只有用两只眼镜看物体才能产生立体感, 如果用两个镜头如人眼那样, 从两个不同的方向同时摄下电影场景的像, 制成正片. 在放映时通过两个放映机用振动方向互相垂直的两种线偏振光重叠地放映到银幕上, 人眼通过上述的偏振眼镜观看, 每只眼睛只能看到相应独立的一个图像, 就会像直接观看时那样产生立体的感觉
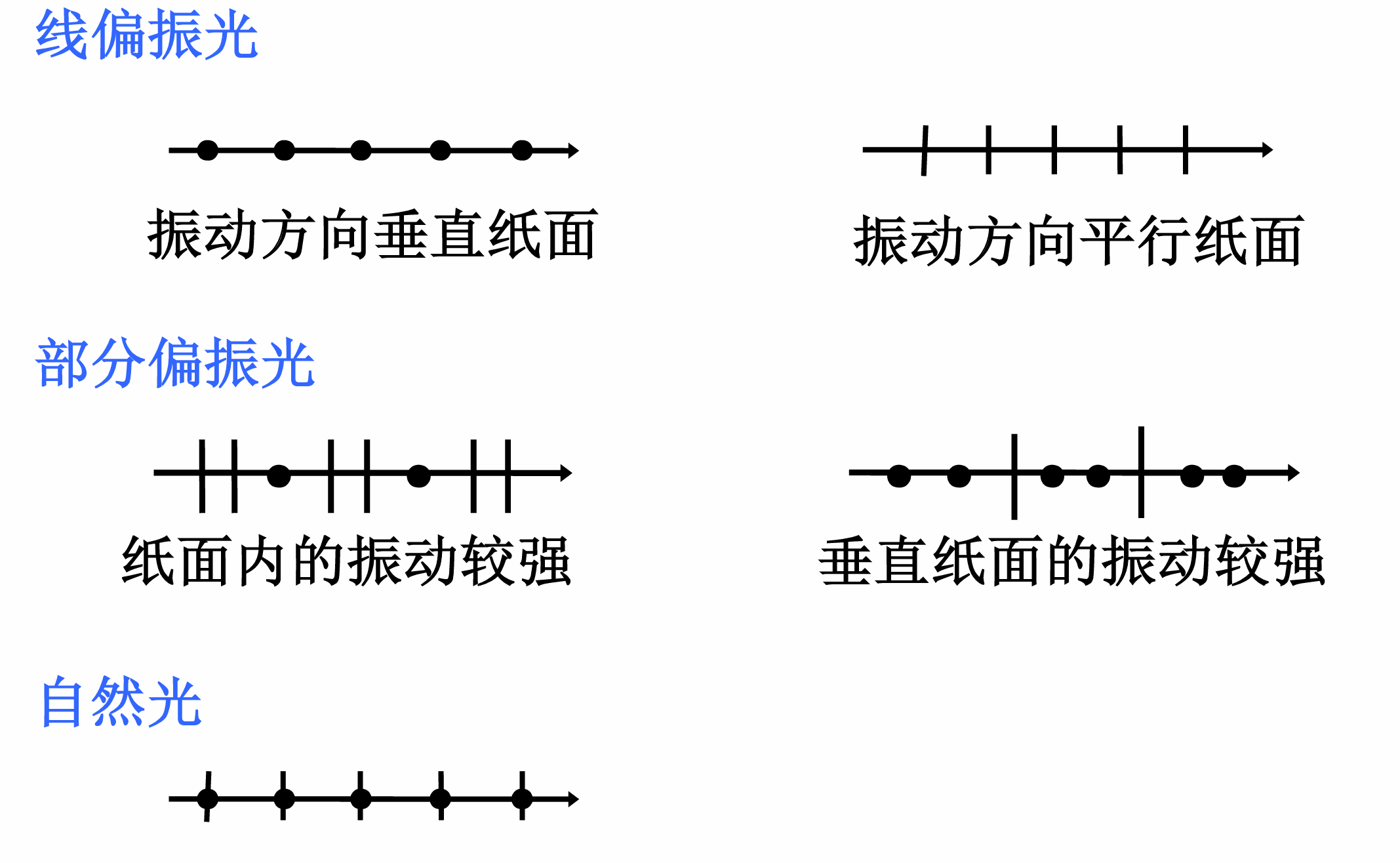
自然光
光场中的任一点、任一传播方向, 都同时存在着大量各种随机取向的横振动, 且没有固定的位相差, 因而, 在与传播方向垂直的任一方向上的振动都是相等的. 这类型的光称为自然光. 一般的热辐射光源发出的光波都是自然光
线偏振光
只包含单一振动方向的光称为线偏振光或面偏振光. 其振动方向和传播方向构成的平面称为振动面
Malus 定律
线偏振光在其它方向上的振动分量同其与振动面夹角余弦的平方成正比, 即:
由于自然光可以看作是互相垂直的两个平面偏振光的叠加, 所以自然光透过偏振片后, 可以看作是平行于偏振片偏振方向的那一部分通过, 垂直的那一部分不能通过, 所以透过的光强变为原来的一半
部分偏振光
若在各不同方向的横振动中, 某一方向占有优势, 这类光波称为部分偏振光
部分偏振光光强极大方位和光强极小方位总是正交的
部分偏振光是介于自然光和线偏振光之间的一种状态. 部分偏振光的偏振程度用偏振度来衡量:
当时, 称之为自然光(非偏振光) 当时, 称之为线然光(全偏振光)
偏振光的图示标记方法
圆偏振光
电矢量在垂直传播方向的平面内作匀速转动, 其端点扫出一个圆形的轨迹, 这类光波称为圆偏振光
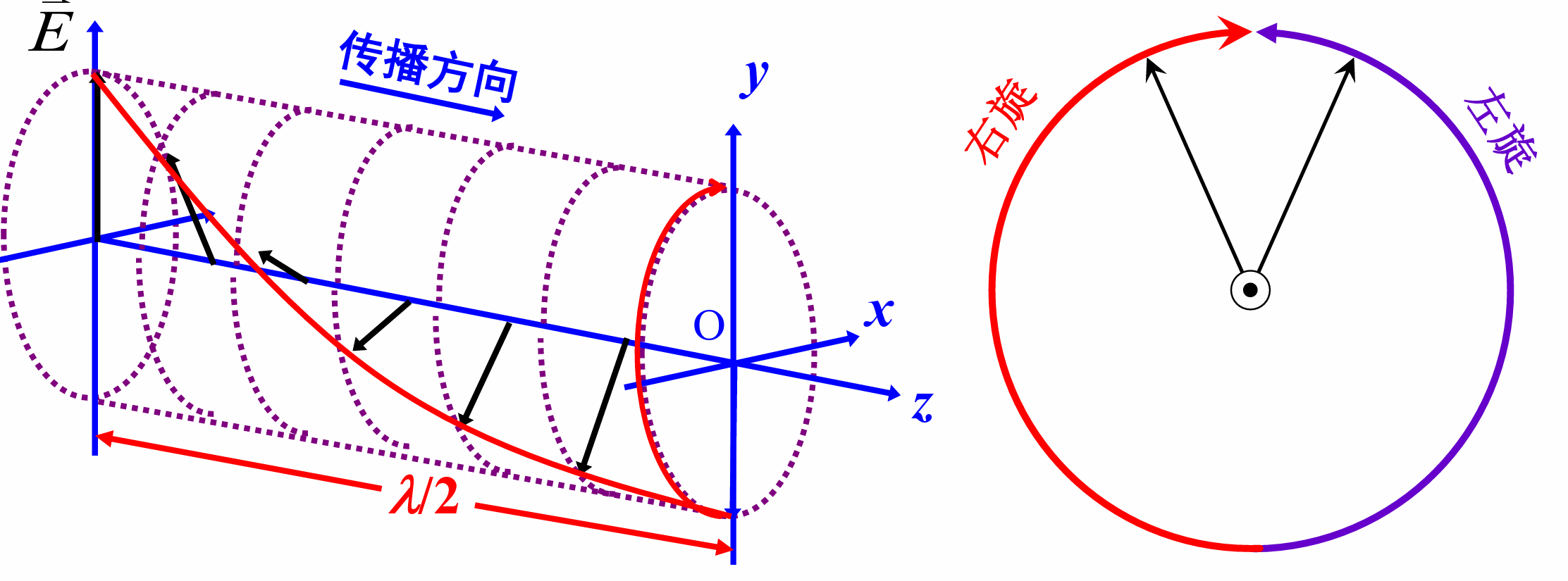 当迎着传播方向观察, 电矢量逆时针转动, 称为左旋圆偏振光;电矢量顺时针转动, 称为右旋圆偏振光.
当迎着传播方向观察, 电矢量逆时针转动, 称为左旋圆偏振光;电矢量顺时针转动, 称为右旋圆偏振光.
两个振幅相等、方向垂直, 相位差的振动的合成振动, 这就是圆偏振光
对应于右旋, 对应于左旋
不能用检偏器区分自然光和圆偏振光
椭圆偏振光
电矢量在垂直传播方向的平面内作匀速转动, 其端点扫出一个椭圆形的轨迹, 这类光波称为椭圆偏振光. 椭圆偏振光也有左旋、右旋的区分, 其定义与圆偏振光相同
两个振幅不等, 方向垂直, 位相差不等于的振动的合成振动, 就是椭圆偏振光
位相差大于对应于右旋, 小于对应于左旋
不能用检偏器区分部分偏振光和椭圆偏振光
Fresnel 方程
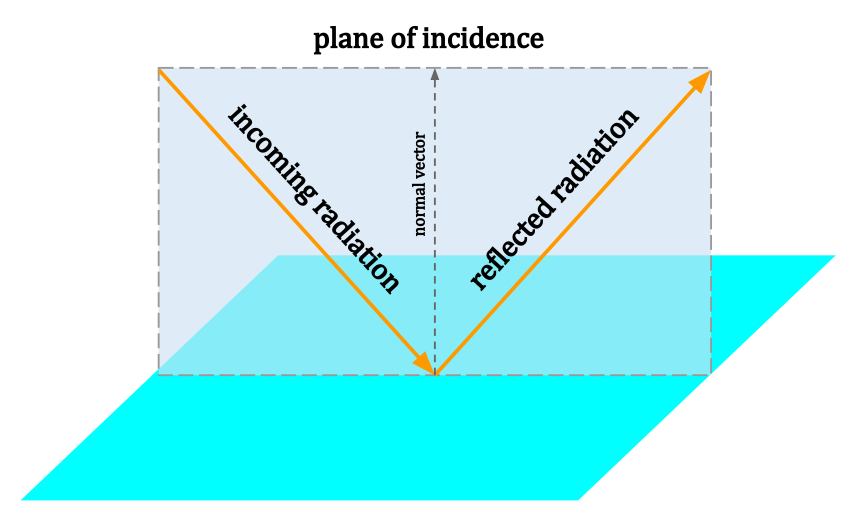
S 和 P 偏振
对于入射波的两个不同的线性偏振分量, 有两组菲涅耳系数. 由于任何偏振态都可以分解为两个正交线性偏振的组合, 因此这足以解决任何问题
s偏振是指垂直于入射面 (plane of incidence)(也就是平行于界面, 下面推导中的方向)的波电场的偏振;那么磁场位于入射平面内. p偏振是指电场在入射面(下面推导中的平面)内的偏振;那么磁场垂直于入射平面.
偏振光的反射率
我们将从界面反射的功率和入射功率的比值称为反射率 , 折射到第二介质中的部分功率和入射功率的壁纸称为折射率
s偏振光的反射率为
p偏振光的反射率为
其中分别是介质的波阻抗
如果介质是非磁性的(即), 那么波阻抗只有折射率决定
由此我们得到
偏振光的透射率
根据能量守恒有
Brewster 角
令, 结合 Snell 定律, 可以得到
这里的 为Brewster 角, 这个时候, 反射光线为完全偏振光, 仅有s方向的振动分量
半波损失
当波从波疏介质垂直入射到波密介质并从波疏介质和波密介质的分界面反射回波疏介质时,反射波在离开反射点时的振动相位相对于入射波到达入 射点时的振动相位相差,也就是发生了相位突变,这种现象称为半波损失
需要了解的结论
- 自然光(部分偏振光)入射 - 反射和折射是部分偏振光
- 圆偏振光(椭圆偏振光)入射 - 反射和折射是椭圆偏振光
- 线偏振光入射 - 反射和折射是线偏振光, 但是振动面有旋转
- 全反射 - 反射光是椭圆偏振光
- Brewster角入射 - 反射光是s线偏振光
干涉
波的叠加和干涉
相干条件
干涉项
要让上面这项不为, 我们有相干条件
- 频率相同
- 存在着相互平行的振动分量
- 存在着稳定的相位差
普通光源发光机制
原子和分子(微观客体)内部的能量改变特点:
- 不同原子或分子所发射的波列在振动方向和位相上相互独立, 没有联系
- 每个原子或分子发光的持续时间极短 所以两个普通光源发出的光波之间很难相干
Note
几个重要的时间间隔:
- 光扰动的时间周期: sec
- 实验观测的时间(人眼的响应时间): sec
- 探测器响应时间: sec
由于 所以**无论是实际观察还是仪器接收, 得到的都不可能是某一瞬间的扰动分布, 而只能是扰动强度的时间平均值, 即强度. **
相干光源和非相干光源:
- 两光源间有固定的位相差, 因而按振幅进行迭加, 那么它们称为相干光源
- 而若两光源之间没有固定的位相差, 因而按强度进行迭加, 则称为非相干光源
反衬度
反衬度(可见度):
Young氏双缝实验
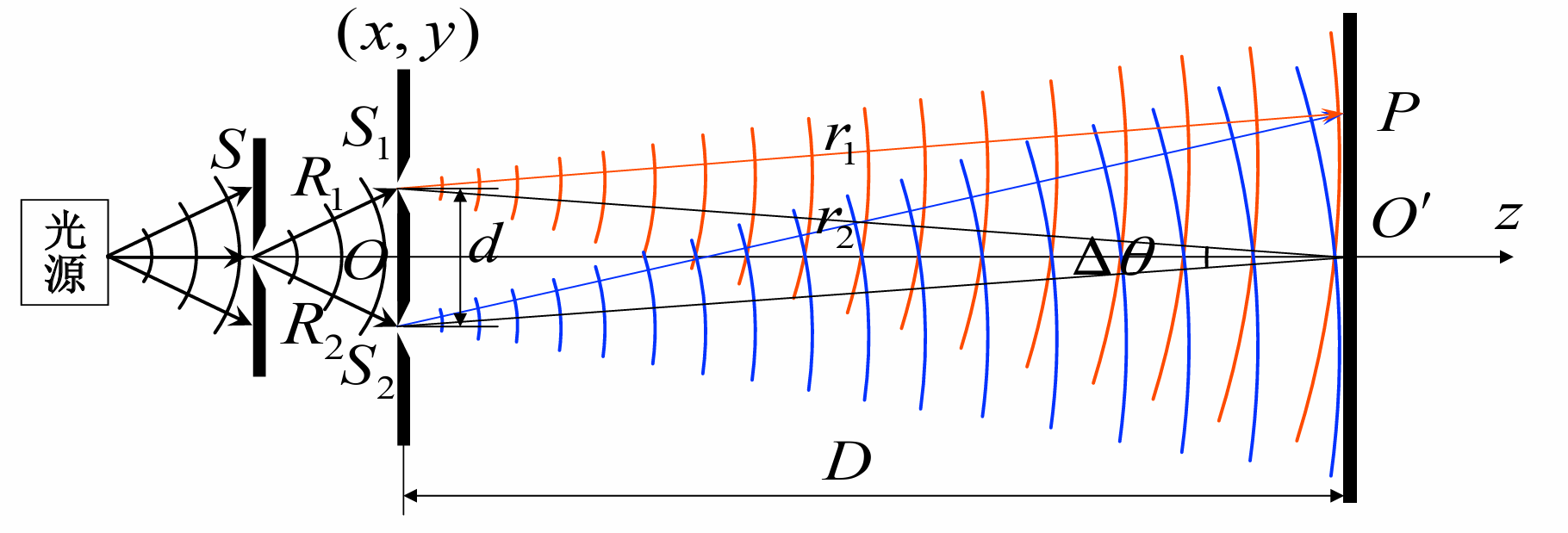 强度分布
强度分布
条纹间距
Young氏实验最重要的一点在于: 利用次光源分解, 巧妙地获得了相干光源
分波前干涉
利用光具组将同一列波分解, 使它们经过不同的途径后重新相遇, 由于这样的两列波由同一列波分解而来, 它们频率相同, 位相差稳定, 振动方向也可做到基本平行, 因而满足相干条件, 能产生干涉图样. 实际的干涉装置按分解波列的方法不同分为两种:
- 分波前法: 将点光源的波前分割为两部分的波列分解法称为分波前法, 杨氏双缝是分波前法的典型代表
- 分振幅法: 利用两种媒质的界面将振幅分解为反射和透射两部分的波列分解法称为分振幅法. 分振幅法的典型代表是薄膜干涉和迈克尔逊干涉仪
杨氏双缝
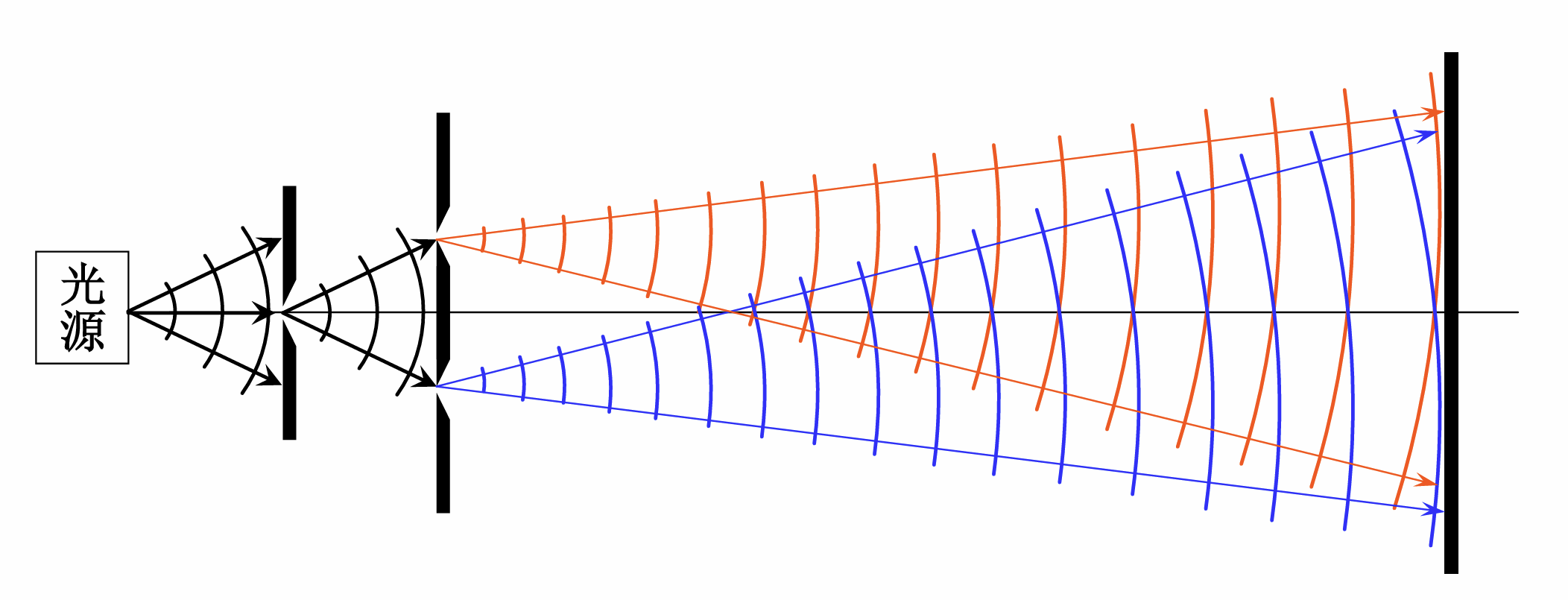
Fresnel 双面镜
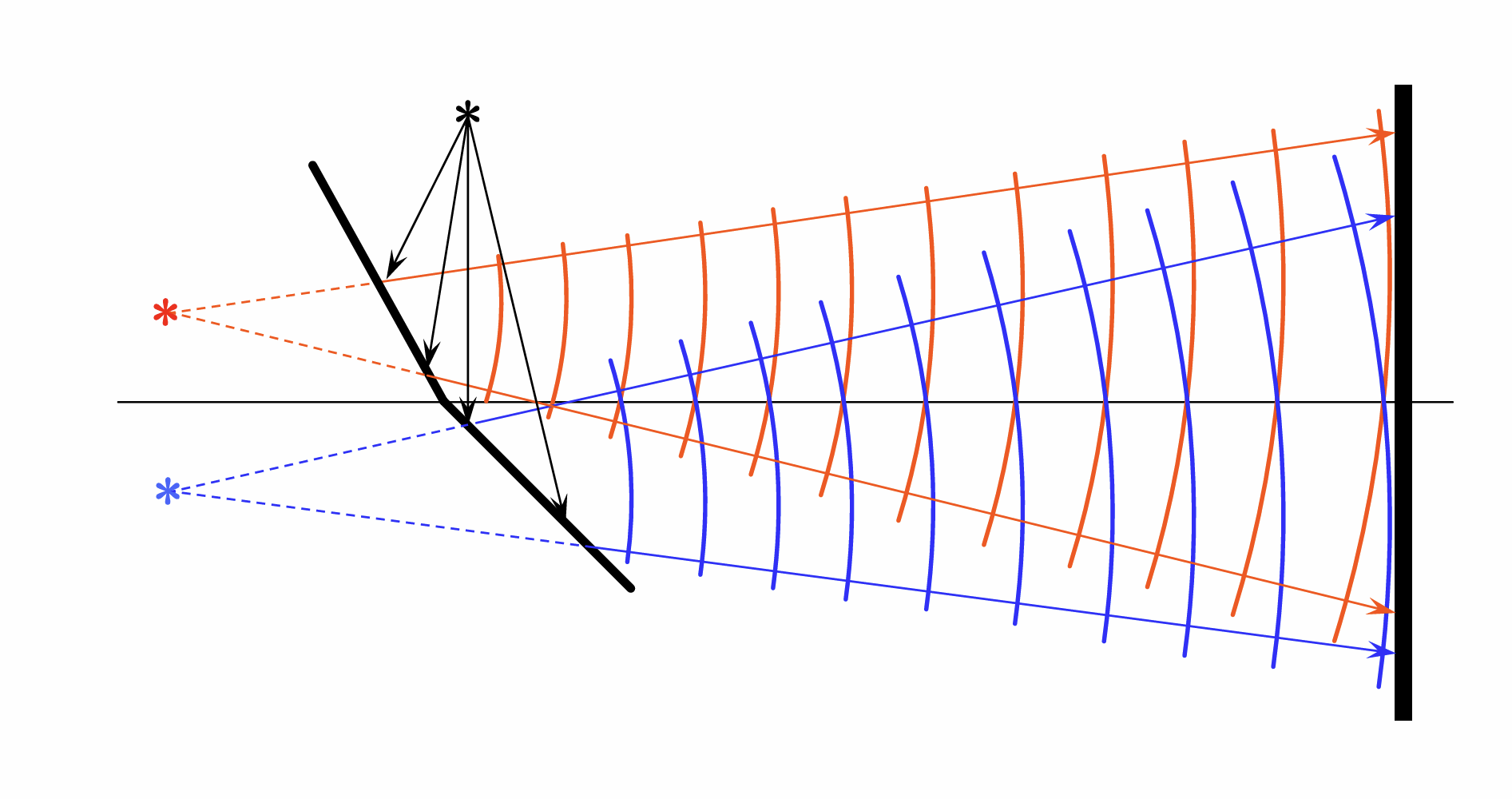
Fresnel 双棱镜
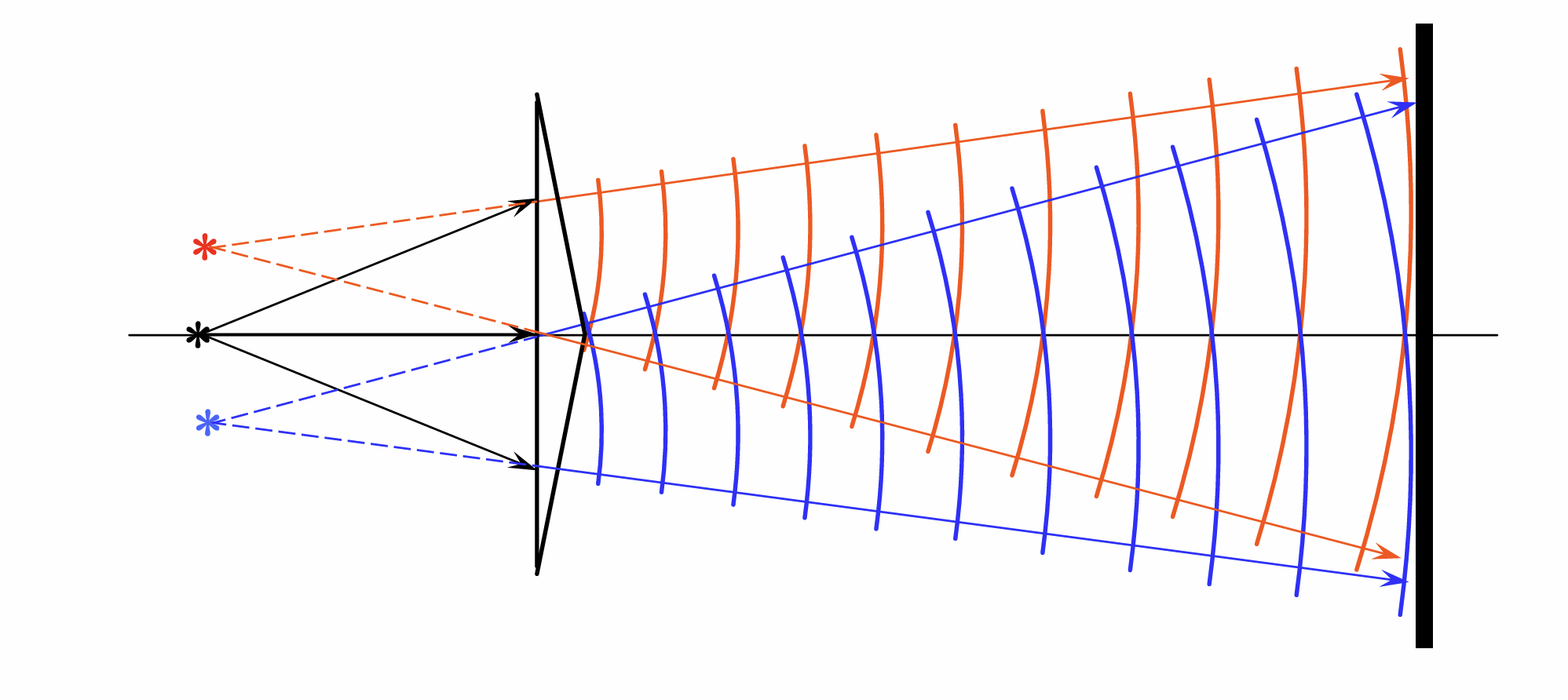
H.Lloyd 镜
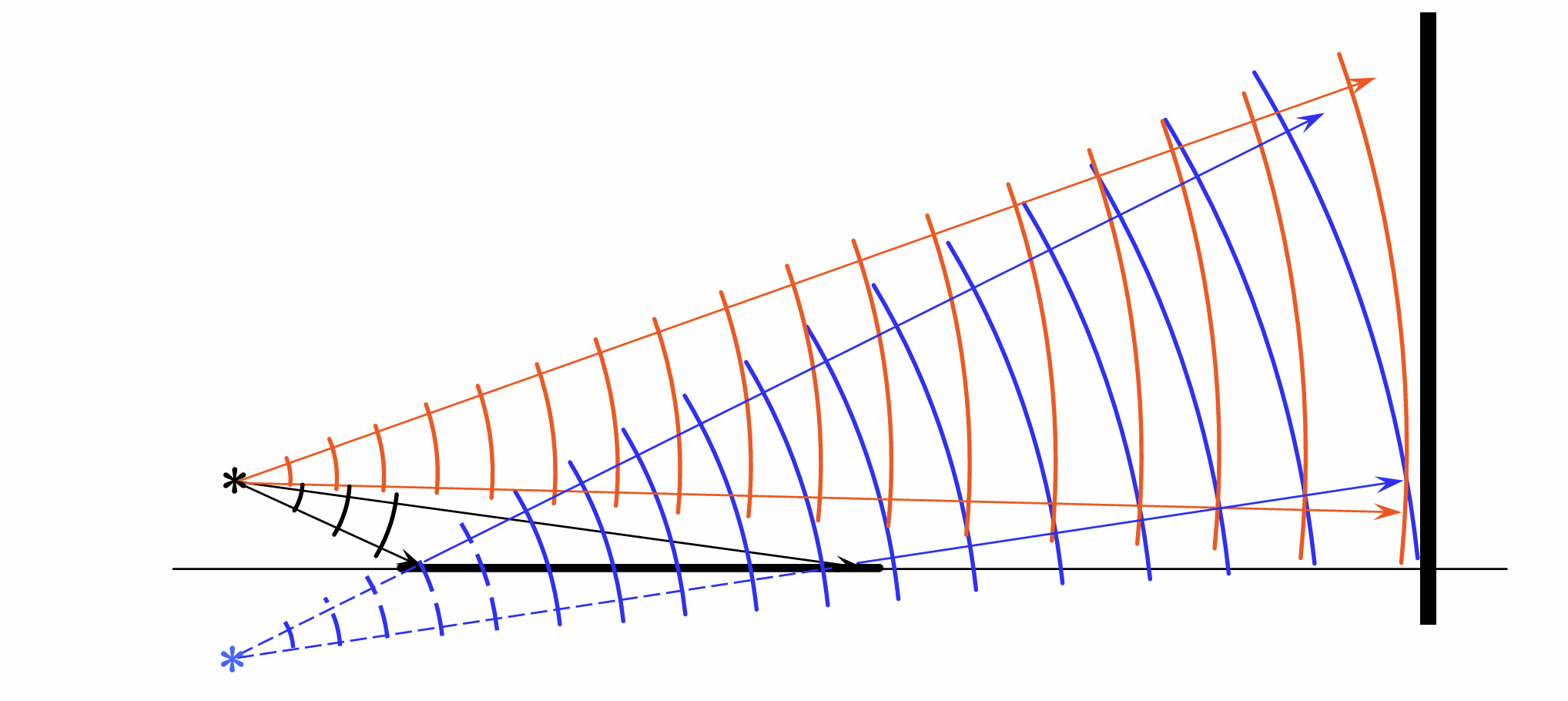
条纹的形状和间距
均为近似的一组平行直线, 间距都可以转化为杨氏双缝的公式
干涉条纹的移动
关键是确定零级亮条纹的位置(相位差为的点)
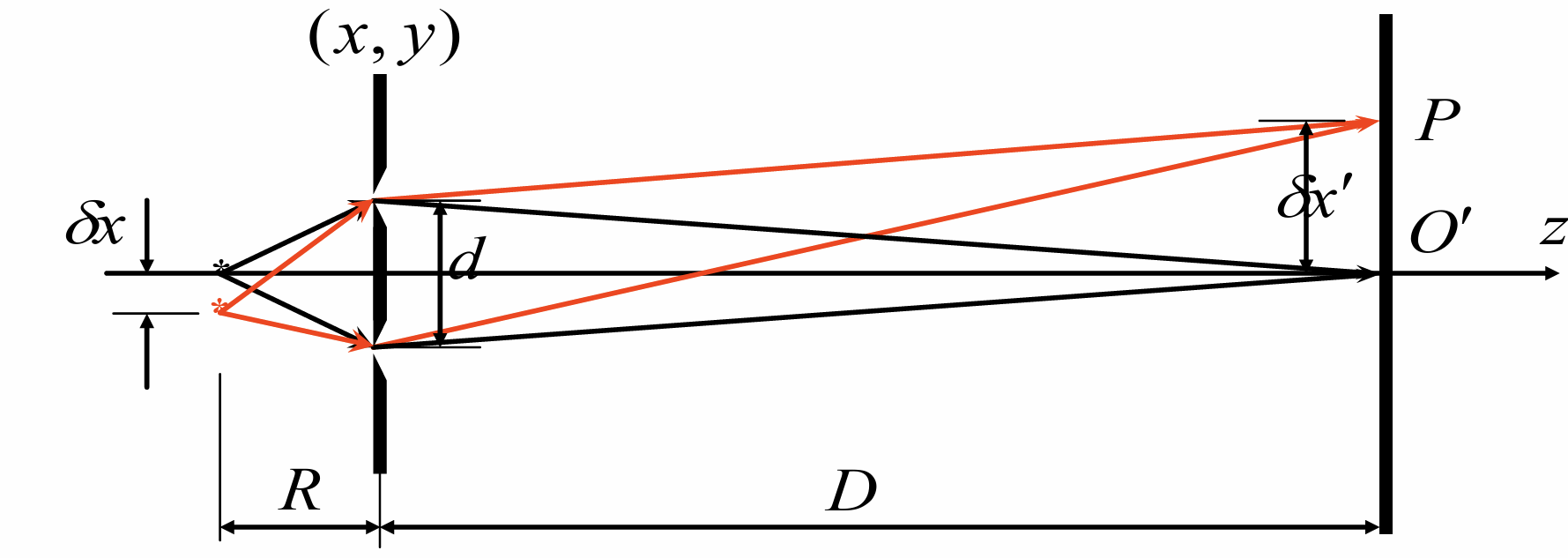 中心条纹移动的距离
中心条纹移动的距离
光场的空间相干性
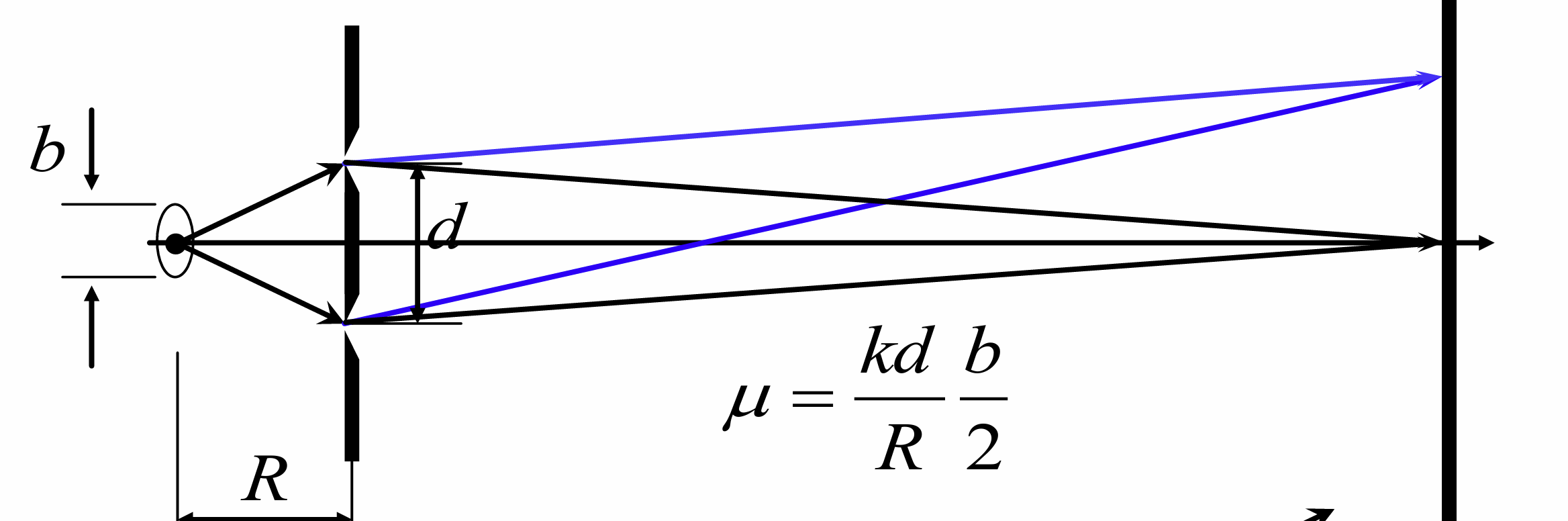 固定光源的宽度不变, 考虑相干场的横向线度(把两个缝看作两个探针), 最大线度约为
固定光源的宽度不变, 考虑相干场的横向线度(把两个缝看作两个探针), 最大线度约为
最大角宽度约为
由此得到空间相干性的反比公式
即相干场对光源的角宽度反比于光源的宽度, 二者的乘积与波长相当
分振幅干涉
等厚干涉
光程差
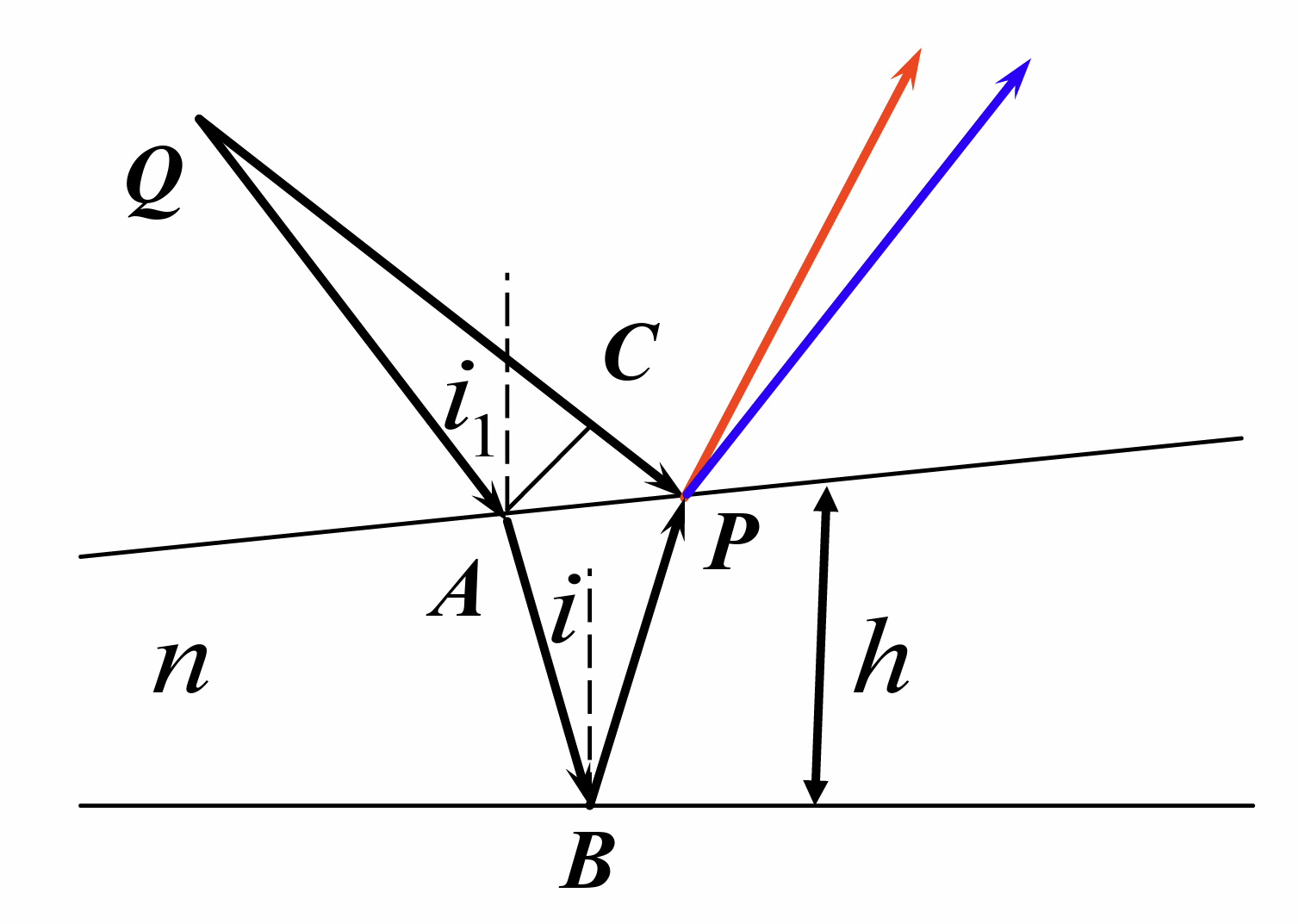
干涉条纹
薄膜表面沿等厚线分布的干涉条纹称为等厚干涉条纹 相邻条纹的厚度差
Newton 环
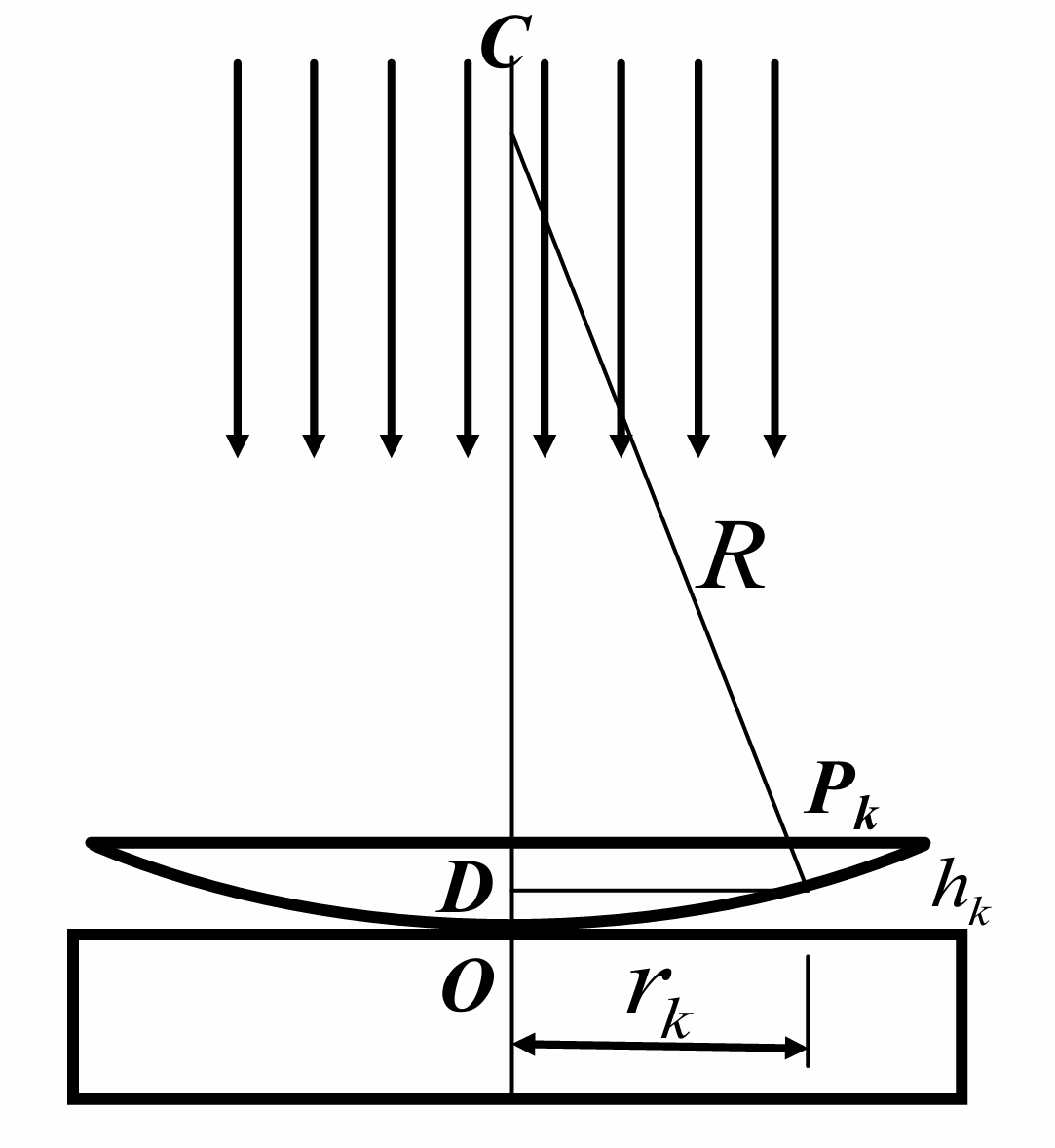 由圆幂定理
由圆幂定理
又光程差
故
因为存在半波损失, 上面的给出的是暗条纹, Newton环的中心是暗条纹
观测方法
严格的等厚干涉要求点光源、正入射. 但扩展光源、斜入射, 用眼睛也能观察到干涉现象. 主要是眼睛的瞳孔对光束进行了限制, 只是干涉的结果会受到一定的影响
条纹偏离等厚线
反衬度降低
眼睛瞳孔限制扩展光源参与干涉的区域. 光源不同处的不同, 越大, 反衬度越低.
薄膜的颜色、增透膜和高反膜
薄膜的颜色
干涉导致不同波长光的反射率不同
增透膜
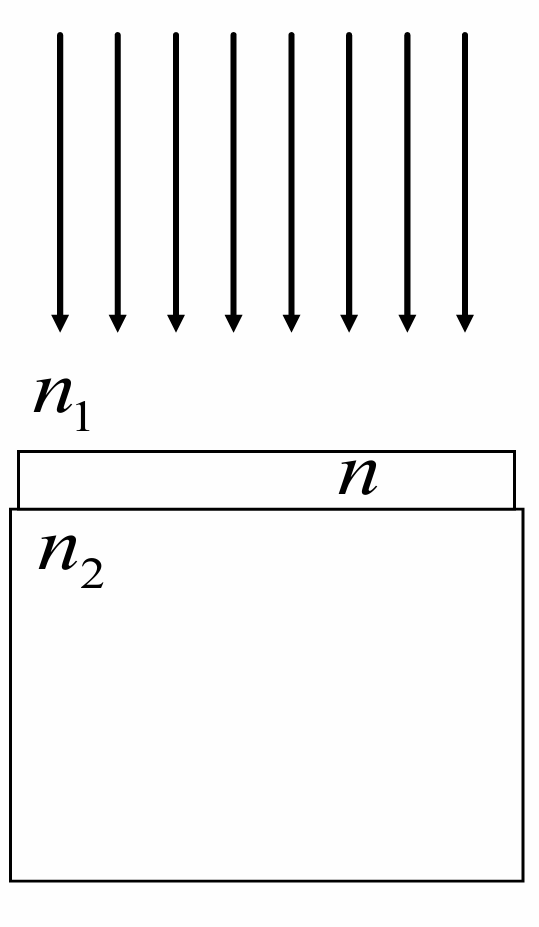 要求
当时完全消除反射光
要求
当时完全消除反射光
高反膜
等倾干涉
固定, 但是变化
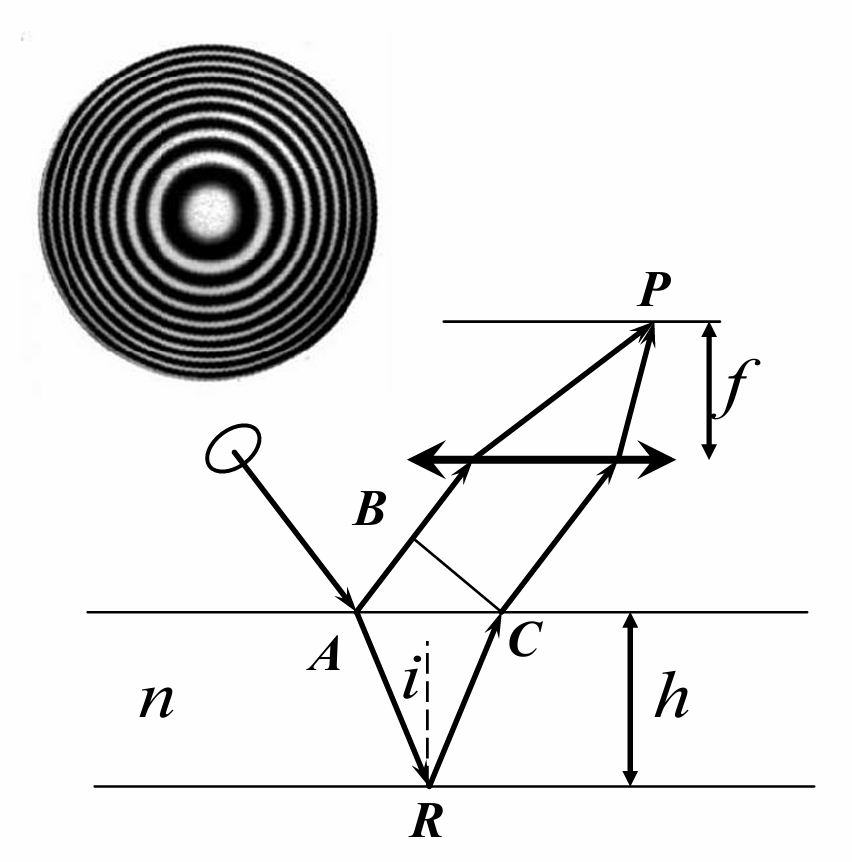
光程差
故
等倾干涉条纹
由薄膜表面等倾角光线形成的干涉条纹称为等倾干涉条纹
倾角相等的条纹会形成一个锥, 在无穷远的光屏上(即某个凸透镜的焦平面)就是同心圆
中心级次高、边缘级次低. 增大, 条纹从中心生出并向外扩展;减小, 条纹向中心会聚并消失于中心
观察等倾条纹时扩展光源的作用
光源上各点形成完全一样的干涉图样(强度相加而不是振幅相加), 其效果是提高干涉图样的亮度, 有益无害. 但是拓展光源对观察等厚条纹会有影响
薄膜干涉的定域问题
点光源照明
上下两束光交迭的任何区域都有干涉条纹存在, 干涉条纹是非定域的
扩展光源照明
只在上下表面反射的两束光交迭的部分区域内可看到干涉条纹, 这种条纹称为定域干涉条纹
定域条纹的范围称为定域深度, 定域深度内有一曲面, 在此曲面上干涉条纹的反衬度最大. 该曲面称为定域中心
干涉条纹的反衬度随偏离定域中心而逐步下降, 直至超出定域范围, 反衬度降为而无法辨认
厚度均匀的薄膜, 定域中心在无限远; 厚度不均匀的薄膜, 定域中心在上下表面附近. 只要对光源宽度有一定的限制(如肉眼观察时眼睛的瞳孔), 即可使薄膜表面进入定域深度之内
无论是等厚干涉, 还是等倾干涉, 既可在薄膜的上方, 也可在薄膜的下方观察到干涉条纹, 只是反衬度不同( 通常为互补)
Michelson 干涉仪
两臂的移动
双线谱
反衬度随光程差周期变化, 变化周期是 如钠黄光这样的双线结构
量程
量程是相干长度的一半
光场相干性小结
产生原因
空间相干性来源于扩展光源不同部分发光的独立性 时间相干性来源于光源发光过程在时间上的断续性
结果
空间相干性主要表现在波场的横向(波前)上, 集中体现在分波前干涉装置中; 时间相干性主要表现在波场的纵向(波线)上, 集中体现在分振幅干涉装置中
反比公式
空间相干性 时间相干性
相干区域和相干时间都不是一个绝对的界限, 实际上相干区域和相干时间内也有非相干的成分, 而相干区域和相干时间之外, 也有相干的成分, 只是主导地位的不同, 部分相干是最为普遍的, 而反衬度则是相干程度的一种度量