Vision Transformers for Dense Prediction

Idea

Assemble token from various stages of the vision transformer into image-like representations at various resolutions and progressively combine them into full-resolution predictions using a convolutional decoder

Transformer vs Convolutions

• Downsampling would lost feature resolution and granularity in deeper stages of the model and can thus be hard to recover in the decoder (May not matter for image classification, but are critical for dense prediction)
• Vision transformer foregoes explicit downsampling operations after an initial image embedding has been computed and maintains a representation with constant dimensionality throughout all processing stages
• The transformer has a global receptive field at every stage after the initial embedding.

Architecture

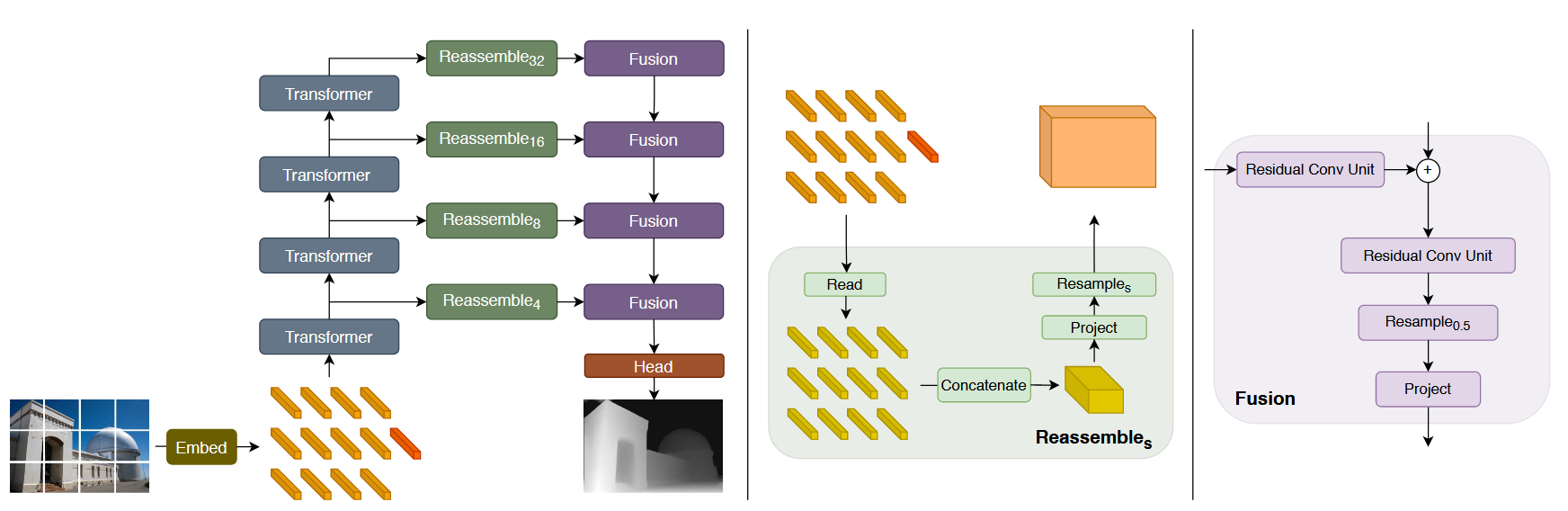
Transformer Encoder

Embedding Method

• Directly flatten the patches into vectors and individually embedded using linear projection
• Alternatively, apply ResNet to the patches and uses the pixel features of the resulting feature maps as tokens

Readout Token

Following work in NLP (such as BERT), the vision transformer additionally adds a special token that is not grounded in the input image and serves as the final, global image representation which is used for classification. We refer to this special token as the readout token

Convolutional Decoder

In the decoder module, we propose a simple three-stage Reassemble operation to recover image-like representation from the output tokens of arbitrary layers of the transformer encoder

Read

First map the $N_p+1$ token to a set of $N_p$ tokens that is amenable to spatial concatenation into an image-like representation.

During this process, the readout token can be either ignored or added to the output tokens

Concatenate

Reshape the $N_p$ tokens into an image-like representation by placing each token according to the position of the initial patch in the image

$$\text{Concatenate}:{\mathbb{R}}^{N_p\times D}\to {\mathbb{R}}^{H/p\times W/p\times D}$$

Resample

Finally pass this representation to a spatial resampling layer that scales the representation to size $\frac{H}{s}\times \frac{W}{s}$ with $\hat{D}$ features per pixel

$${\text{Resample}}_s:{\mathbb{R}}^{H/p\times W/p\times D}\to {\mathbb{R}}^{H/s\times W/s\times \hat{D}}$$

by upsampling convolutional layers

Handling varying image sizes

As long as the image size is divisible by $p$, the embedding procedure can be applied and will produce a varying number of image tokens $N_p$