Fourier 变换基础
见Fourier变换和光学中的Fourier变换
衍射系统和屏函数
凡是能使波前复振幅发生改变的物, 统称为衍射屏
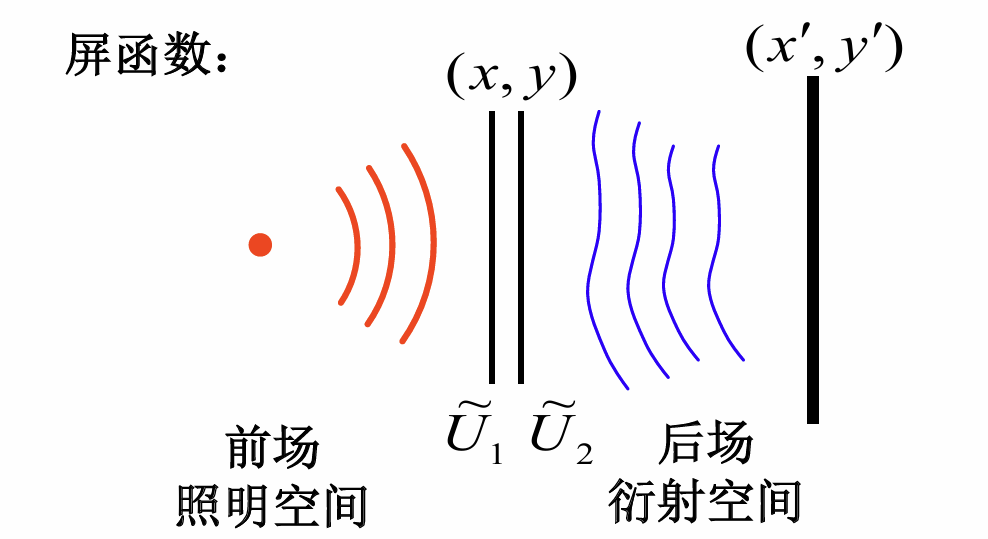 定义屏函数为衍射屏前后表面对应的复振幅之比
定义屏函数为衍射屏前后表面对应的复振幅之比
t~(x,y)=U1(x,y)U2(x,y)
有接收平面上的振幅分布
U(x′,y′)=λ−i∬(Σ0)t(x,y)⋅U1(x,y)reikrdxdy=λ−i∬(Σ0)U1(x,y)reikrdxdy
由于衍射屏函数的作用, 改变了波前, 从而改变了后场的分布, 于是发生的衍射
屏函数的分类
振幅型: t~(x,y)=t(x,y), 特别地对孔或者遮光屏而言
t(x,y)={10透光部分遮光部分
对于一个理想无限小半径的圆孔屏, 它的屏函数可以通过delta函数表示
t(x,y)=δ(x,y)
位相型: t~(x,y)=eiφ(x,y)
相因子判断法
通过相位的表达式eiφ(x,y), 判断一束波的类型
平面波
为常数
发散球面波
exp(ik2zx2+y2)
汇聚球面波
exp(−ik2zx2+y2)
求解屏函数
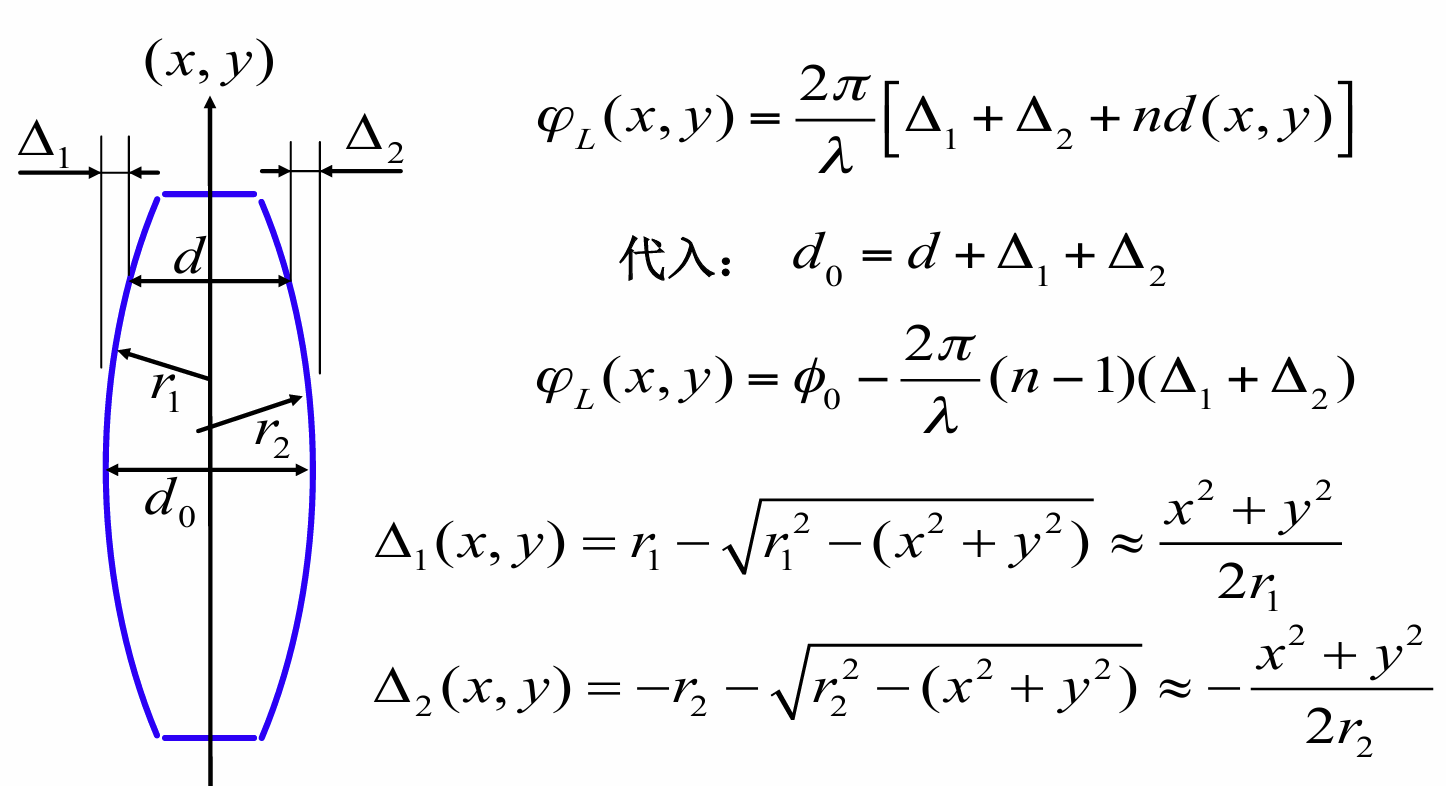 考虑到透镜的磨镜者公式, 有
考虑到透镜的磨镜者公式, 有
φL(x,y)=−λ2π2n−1(r11−r21)(x2+y2)=−k2Fx2+y2
其中
F=(n−1)(r11−r21)1
这是透镜屏函数
对于正入射平面波U1(x,y)=A1=const
有
U~2(x,y)=U~1(x,y)t~L(x,y)=A1e−ik2Fx2+y2
这是会聚在透镜后距离F处的球面波, 和几何光学一致
正弦光栅
空间频率
某一面内光场随空间位置的周期性变化
U~(x,y)=Aeiksinθx=Aeiqxx
有
- 时间周期T⟺空间周期d
- 时间频率ν=T1⟺空间频率f=d1
- 时间圆频率ω=2πν⟺ 空间圆频率q=2πf
二维的情况
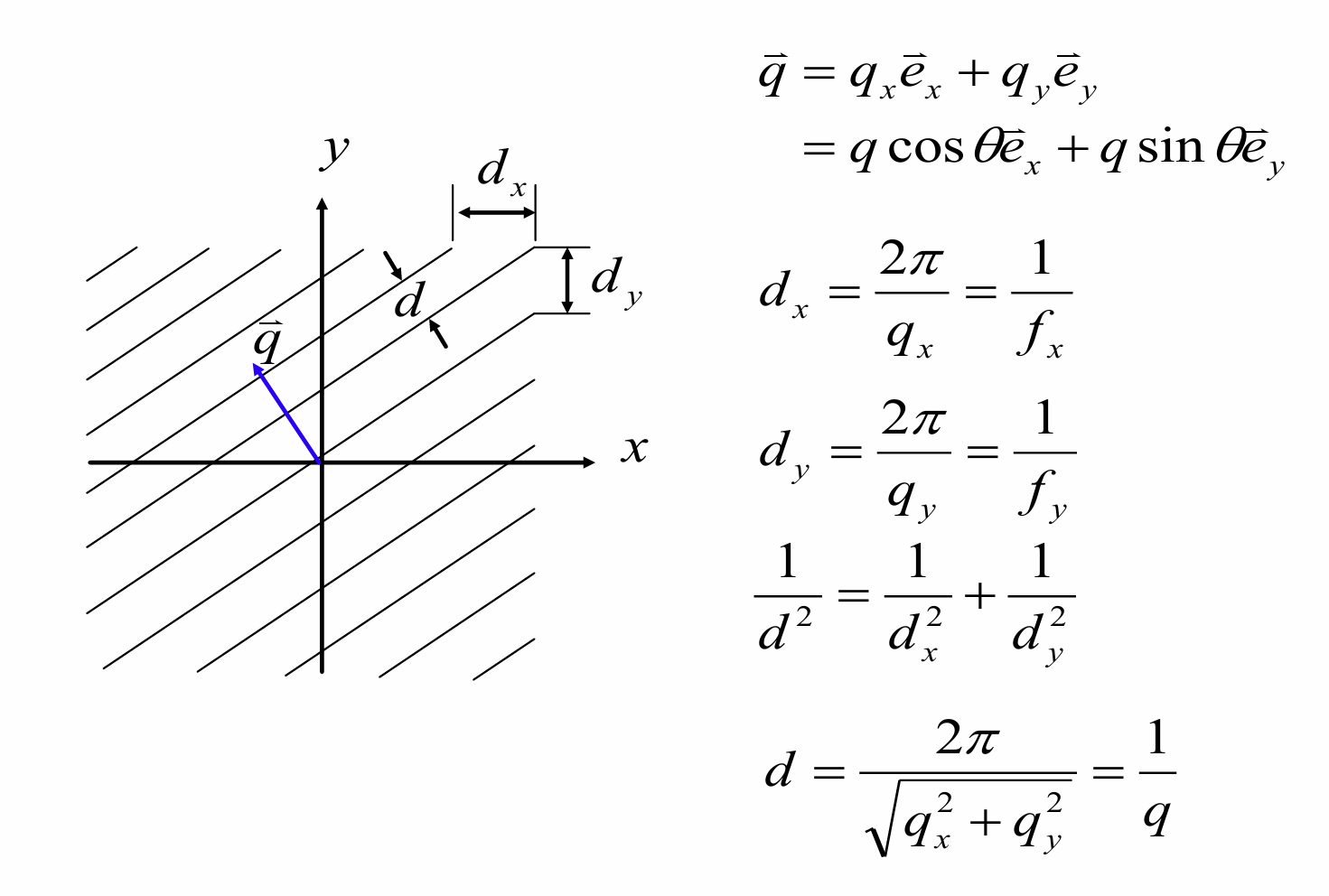
正弦光栅定义
就是透过率是空间的正弦函数的光栅
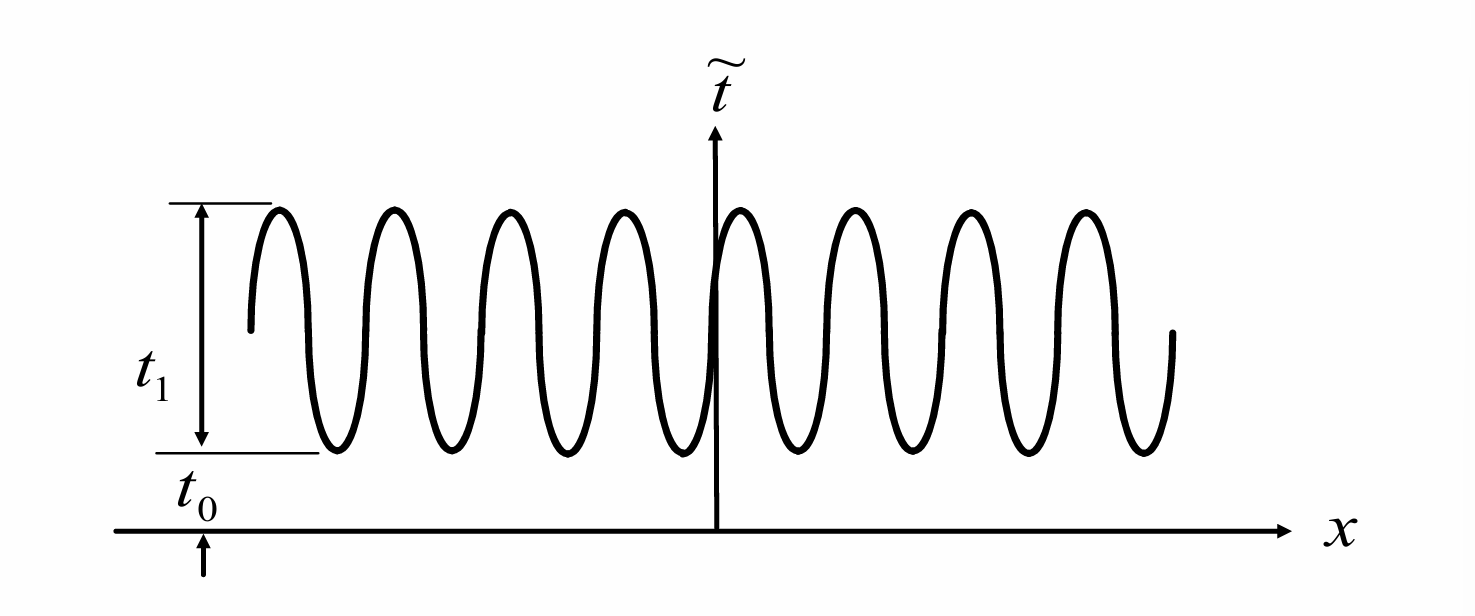
t~(x,y)=t0+t1cos(qxx+qyy+φ0)
正弦光栅的衍射图样
考虑平行光入射U1A1
U2(x,y)=U~1(x,y)t~(x,y)=A1[t0+t1cos(2πfx+φ0)]=A1t0+A1t12ei(2πfx+φ0)+e−i(2πfx+φ0)=U~0(x,y)+U~+1(x,y)+U~−1(x,y)
由相因子判断出射光为三个不同方向的平面波, 其中sinθ±1=±fλ
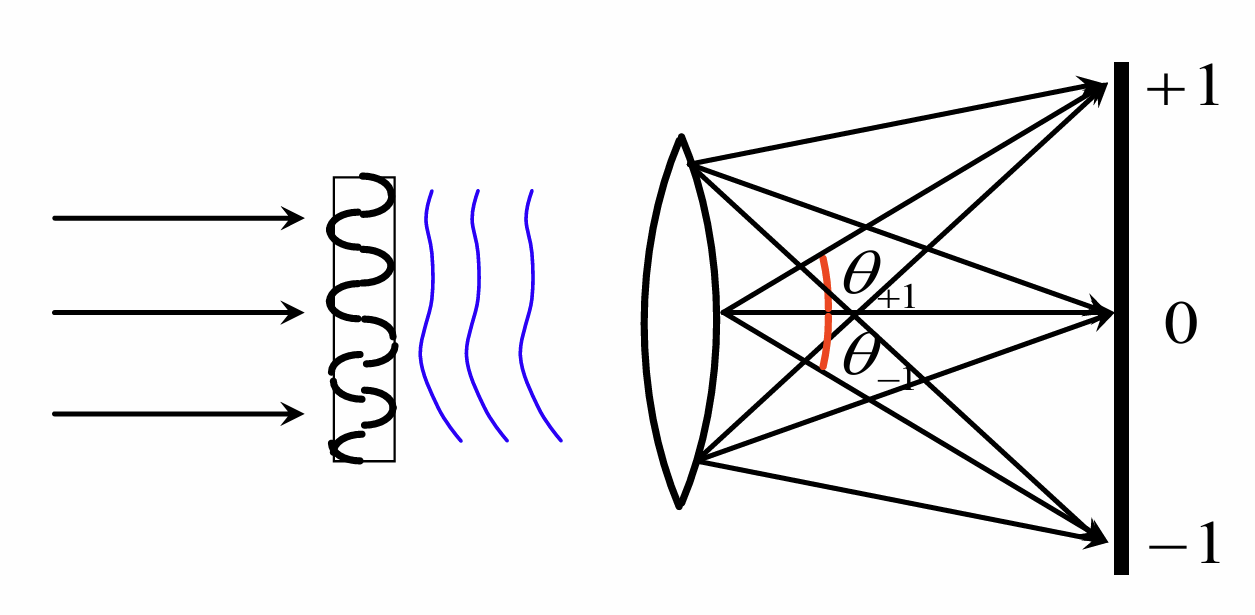
任意光栅的屏函数
利用Fourier展开把任意光栅的屏函数展开为正弦光栅的屏函数的叠加
t(x)wheretn=n=−∞∑∞tnei2πnfx=d1∫−d/2d/2t(x)e−i2πnfxdx
例子: 黑白光栅
设光栅常数为d, 缝宽为a
t(x)={1,0,∣x∣<a/2∣x∣>a/2t0=d1−a/2∫a/2dx=dat~n=d1∫−a/2a/2e−i2πnfxdx=daπfnasinπfna=danπfasinnπfa=danπa/dsin(nπa/d)
对于正入射平行光U1(x)=A1
U2(x)=U~1(x)t~(x)=A1t~(x)=A1t0+A1n=0∑tnei2πnfx
在n级平面波衍射方向
sinθn=nfλ=dnλIn∝t~n2=(da)2(ansinan)2an=πasinθn/λ 定义屏函数为衍射屏前后表面对应的复振幅之比
定义屏函数为衍射屏前后表面对应的复振幅之比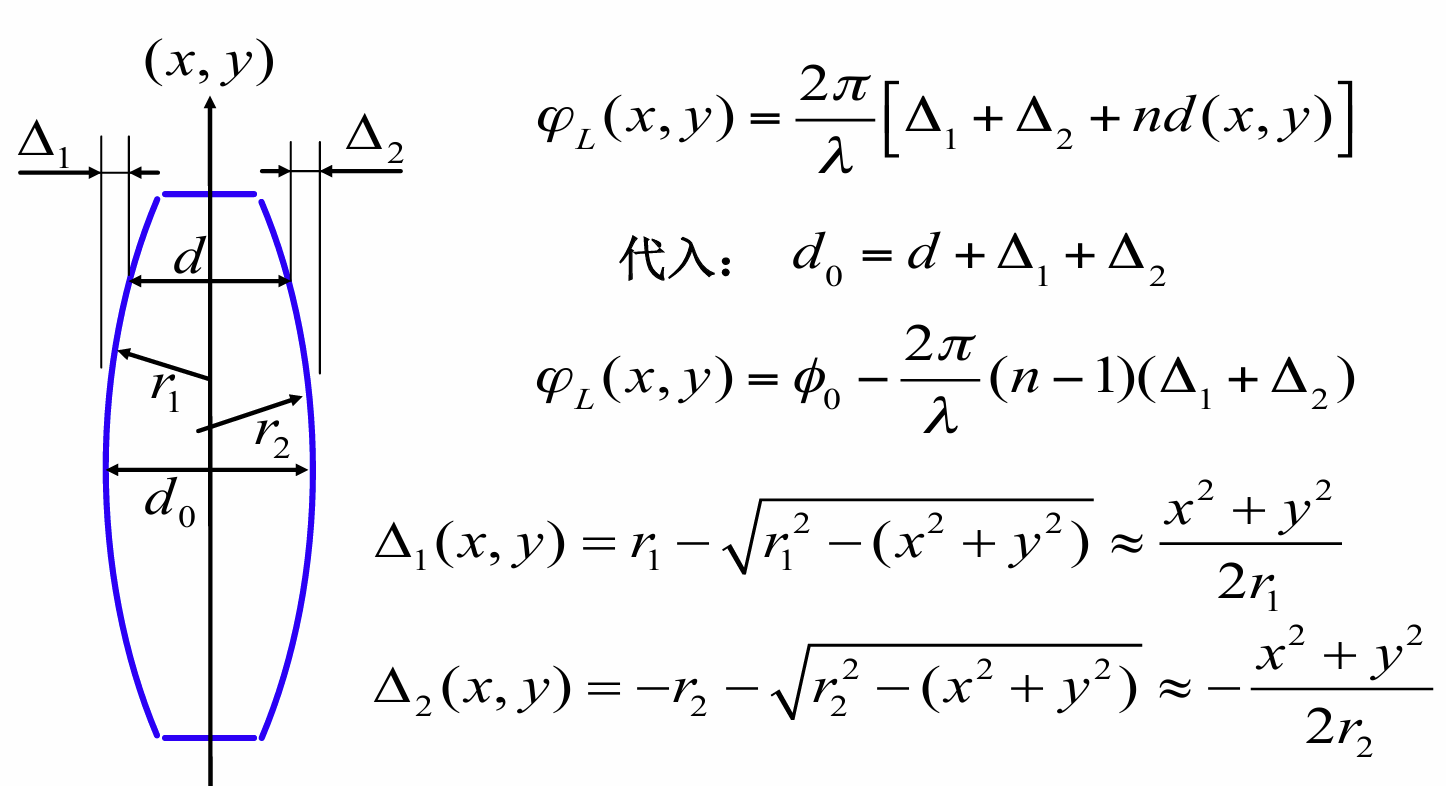 考虑到透镜的磨镜者公式, 有
考虑到透镜的磨镜者公式, 有

