光学的空间形式
在Fourier光学中, 我们把Fourier变换
改写为
来更加方便地处理空间的周期函数, 其中是角空间频率, 对于一列无穷长的波而言其空间频率就是波长的倒数, 这时候它的角空间频率和波数恰好是相等的
并定义如下Fourier变换算子
和逆Fourier变换算子
则有
二维变换
和
其中分别是沿着两个坐标轴的角空间频率
考虑如下情形
无限黑白地砖
想象一个由黑白交错的正方形地砖铺成的无限大地板, 地砖的边长为, 它的边分别平行于轴和轴, 这时候这个图案在轴上的周期均为, 它就可以表示为一个二维的Fourier级数
有限黑白地砖
如果地砖是有限大的, 那么图案就不能是在整个空间中呈周期性, 所以Fourier级数必须用Fourier积分来替代. 上述的二维Fourier变换公式告诉我们, 可以被表示为一系列二维复周期函数的线性组合, 其中的每一项都由一个复数权重确定
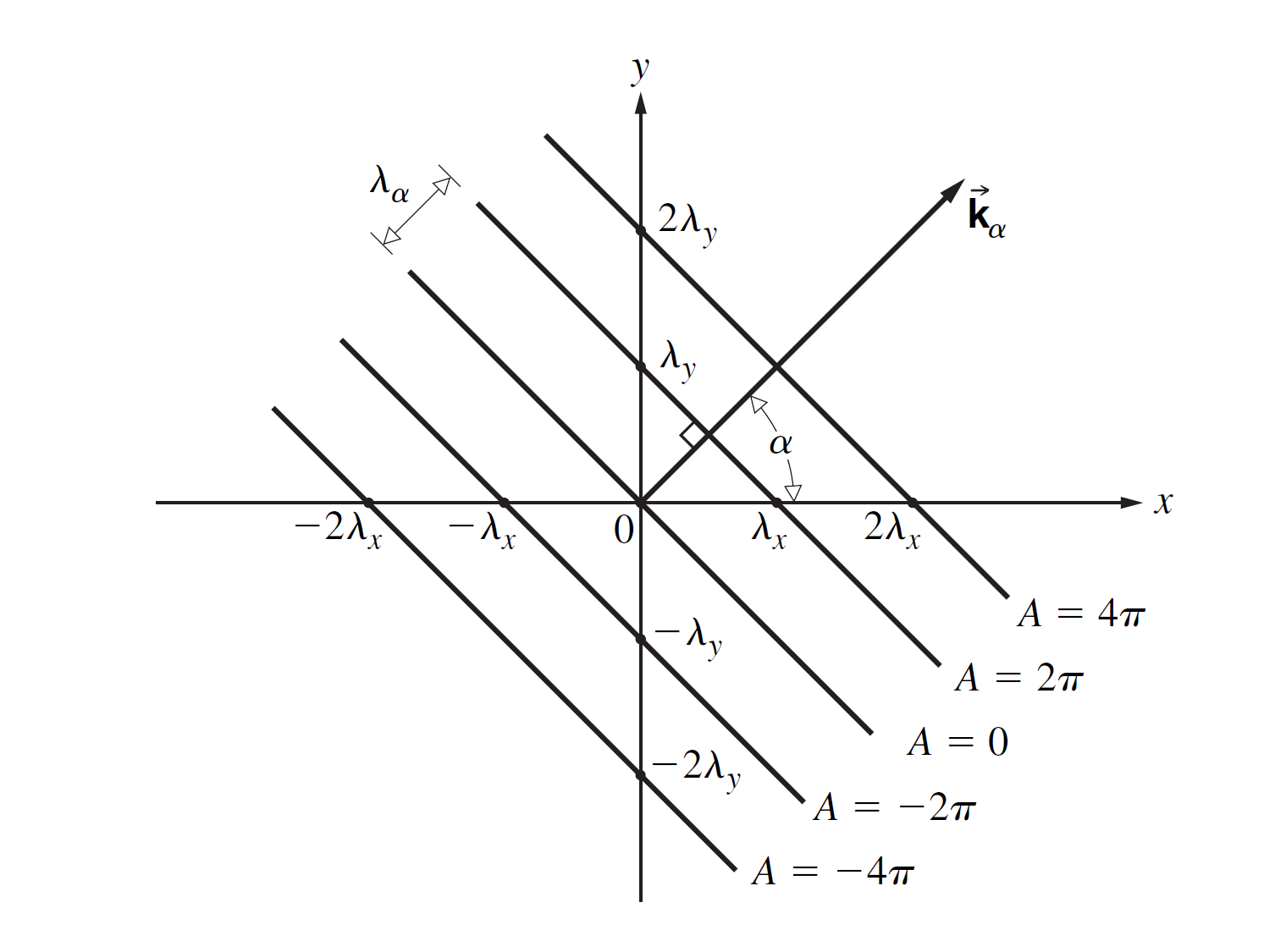
考虑这个复周期函数的等相位线, 也就是
由几何关系容易得到这是一条法向量为的直线, 其中
是整个二维平面呈现的角空间频率, 这里表示和轴的夹角
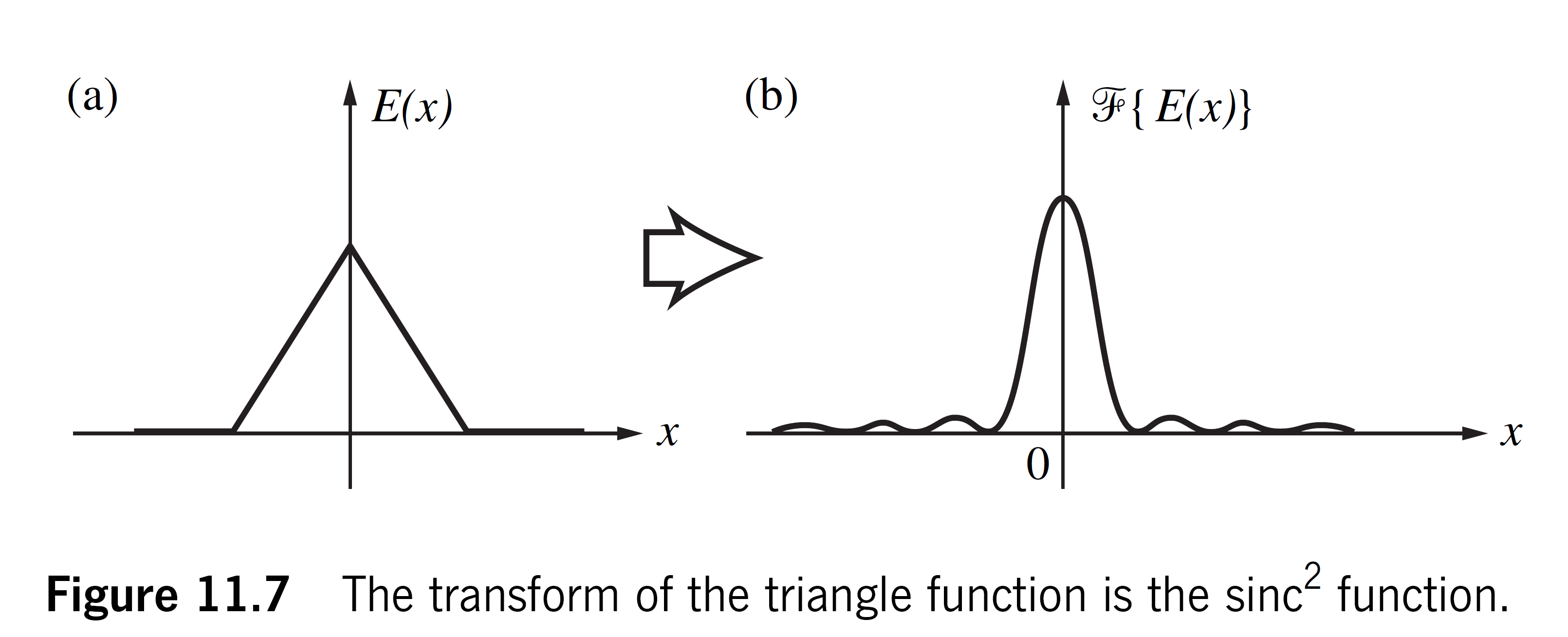
柱函数的Fourier变换
柱函数
的Fourier变换和圆孔衍射存在关联. 由于函数在极坐标系中式对称的, 故令
则有Fourier正变换
由对称性, 这个积分应当和无关, 故选取, 则有
其中表示阶Bessel函数, 再利用变量代换就可以积分得到
这个和Fraunhofer衍射得到的光强大小
十分相似
光具作为实现Fourier变换的元件
在上面的例子中的相似性来自于一个衍射圆孔的作用就近似于把一列表现为圆柱函数的波(只有在孔径内的光波才能通过)变成上面的新函数分布, 而这个函数分布表现为光强呈现在屏幕上就成为了我们所观察到的衍射图样.
事实上, 每一个光具(透镜、孔、遮光屏)等等都可以看作是实现Fourier变换的工具, 一列波通过后就会变成Fourier变换后的形式
Dirac 函数
参见Dirac Delta Function, 这里我们介绍函数在Fourier变换下的性质, 如果对常数进行Fourier逆变换, 则有
在实数域上可以把想象成无数的叠加, 其在时总是取极大值, 叠加结果自然也趋于正无穷大
利用函数的平移性质可以得到
这说明了各个正弦函数的权重仍然是一个常数, 其振幅大小依然是, 但是相位发生了改变. 这告诉我们, **当一个函数在空间(或时间)上发生位移时, 其傅立叶变换等于该函数未发生位移时的傅立叶变换乘以一个相位呈线性变化的指数函数. **
拿一个矩形波举例子, 如果它要进行如下图中的平移, 那么第一个角空间周期为的正弦函数需要有的相位移动
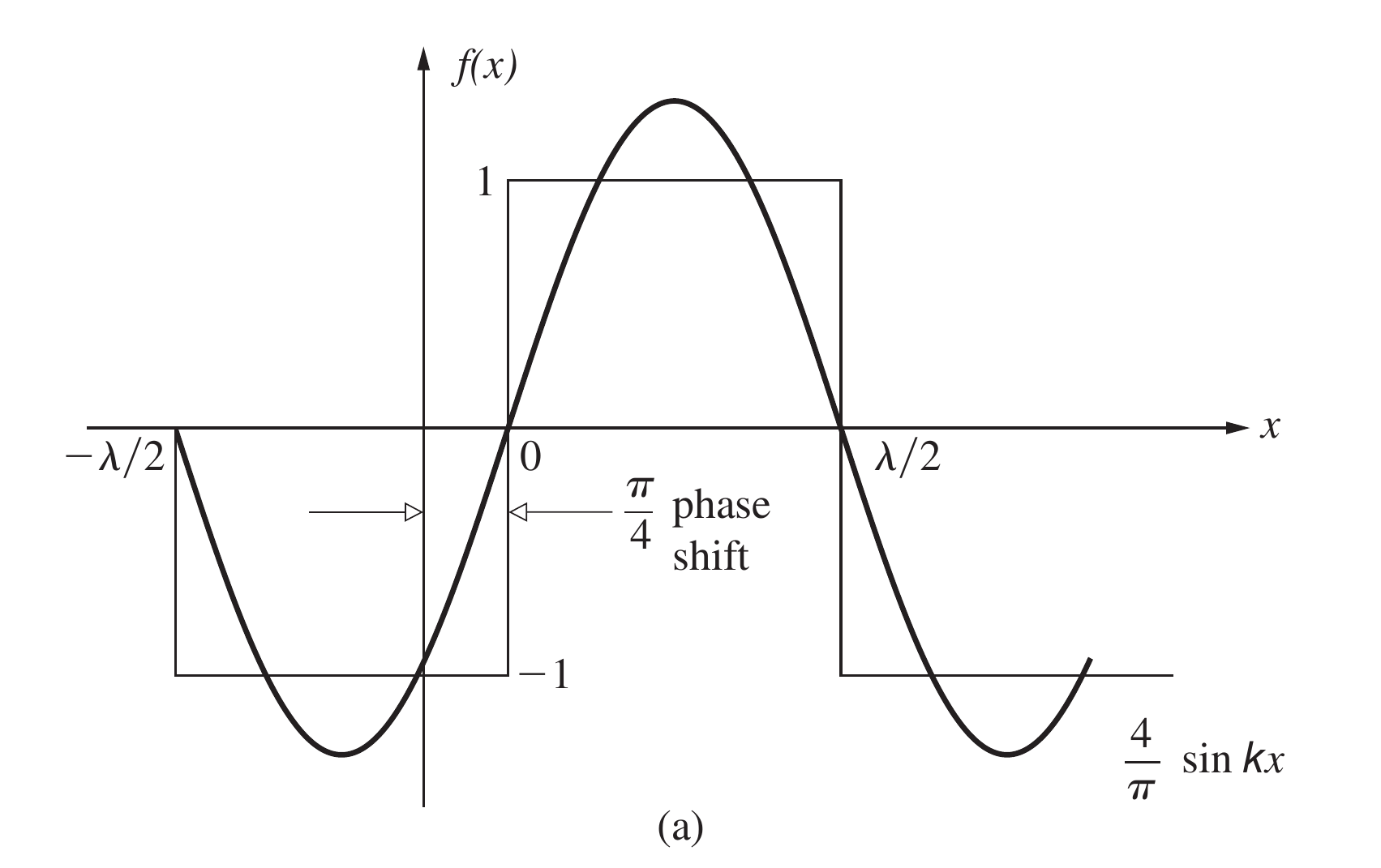 第而个角空间周期为的正弦函数需要有的相位移动
第而个角空间周期为的正弦函数需要有的相位移动
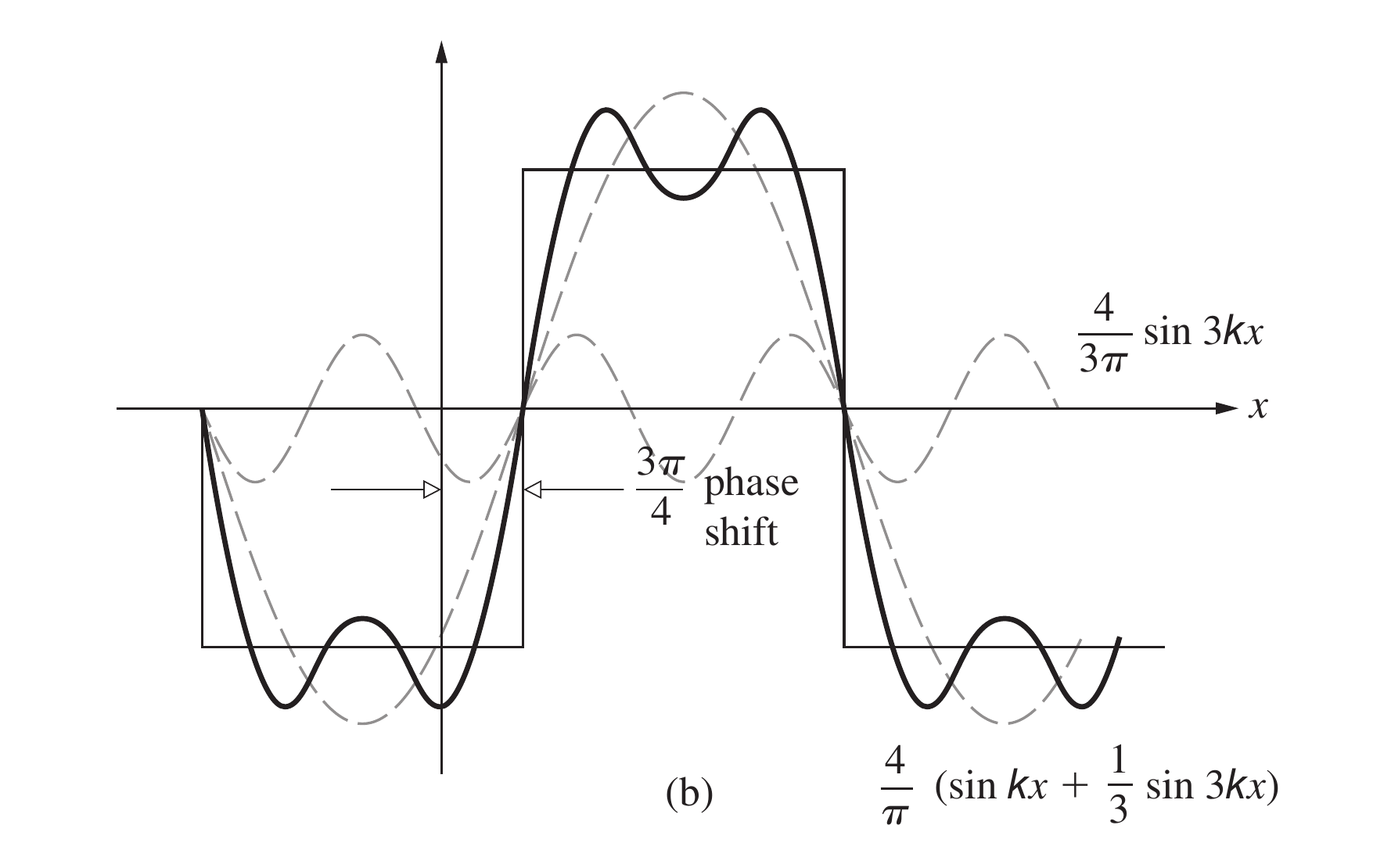 第三个角空间周期为的正弦函数需要有的相位移动
第三个角空间周期为的正弦函数需要有的相位移动
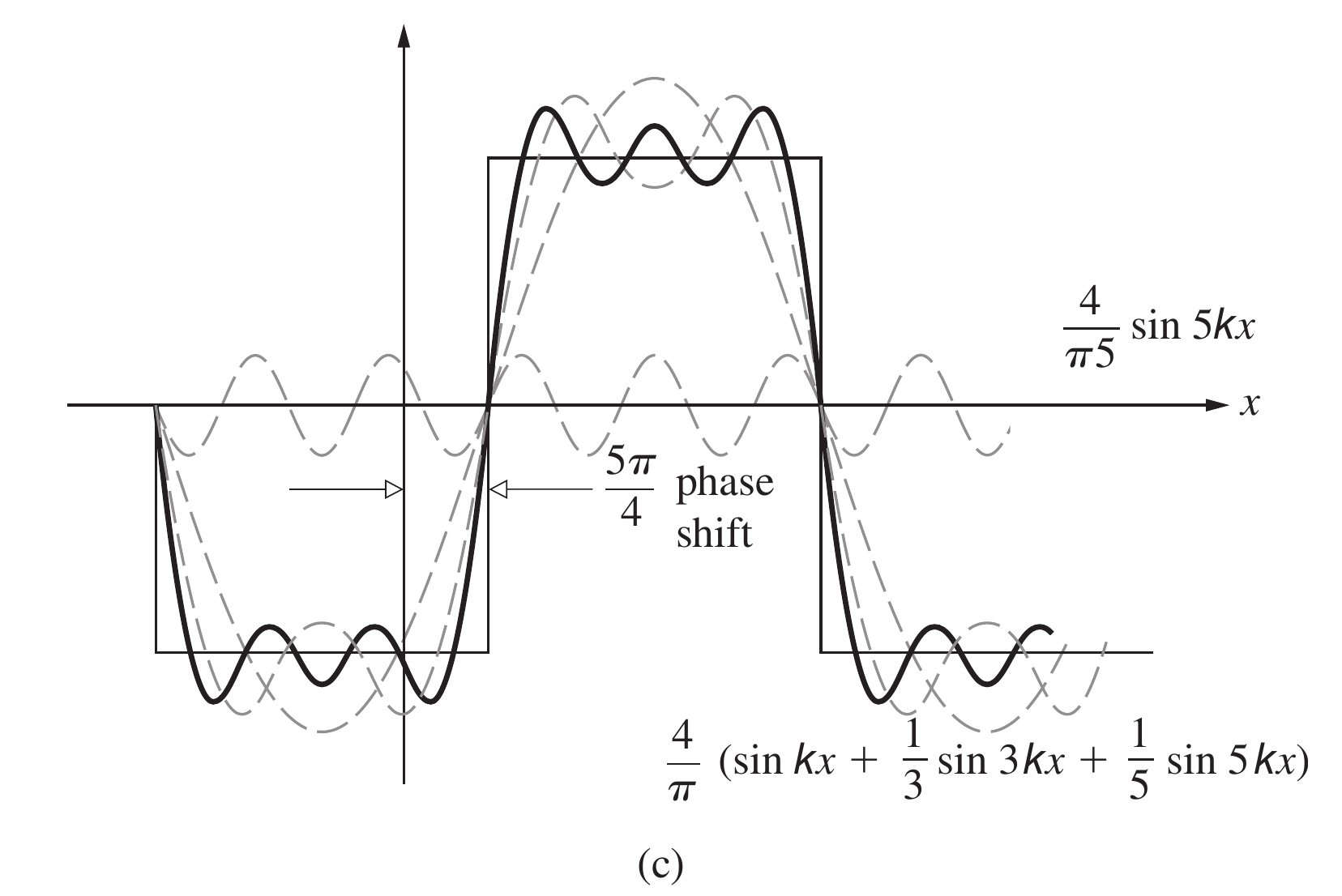
正弦和余弦函数
对于形如
的函数, 它的Fourier变换就是每个函数的变换的和. 于是, 如果我们考虑
则有
由Euler公式就有
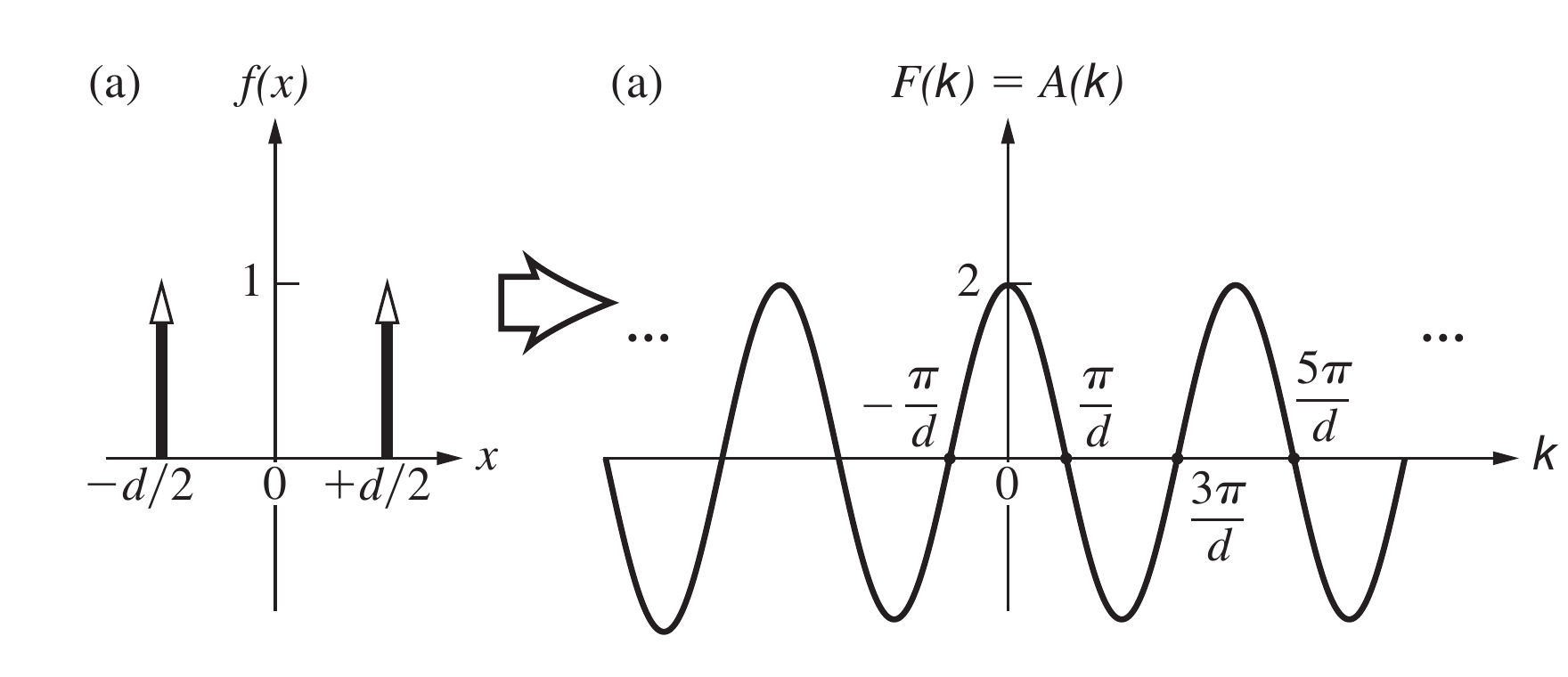 同理我们有
同理我们有
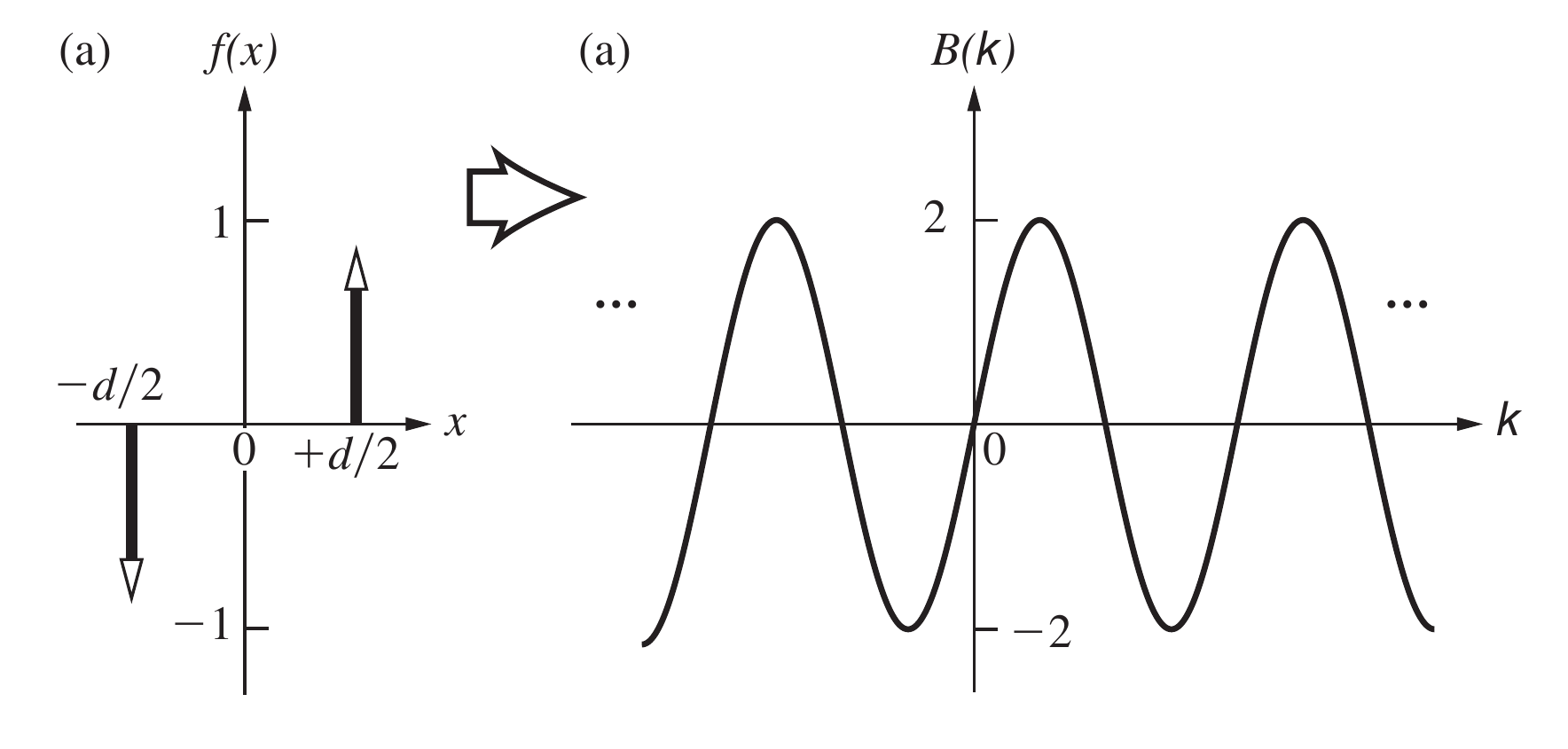 反过来, 弦函数在Fourier变换后可以清晰地得到它的频谱 .
类似于
反过来, 弦函数在Fourier变换后可以清晰地得到它的频谱 .
类似于
我们可以计算得到
于是有
如果选用空间频率而不是角空间频率, 则有 和
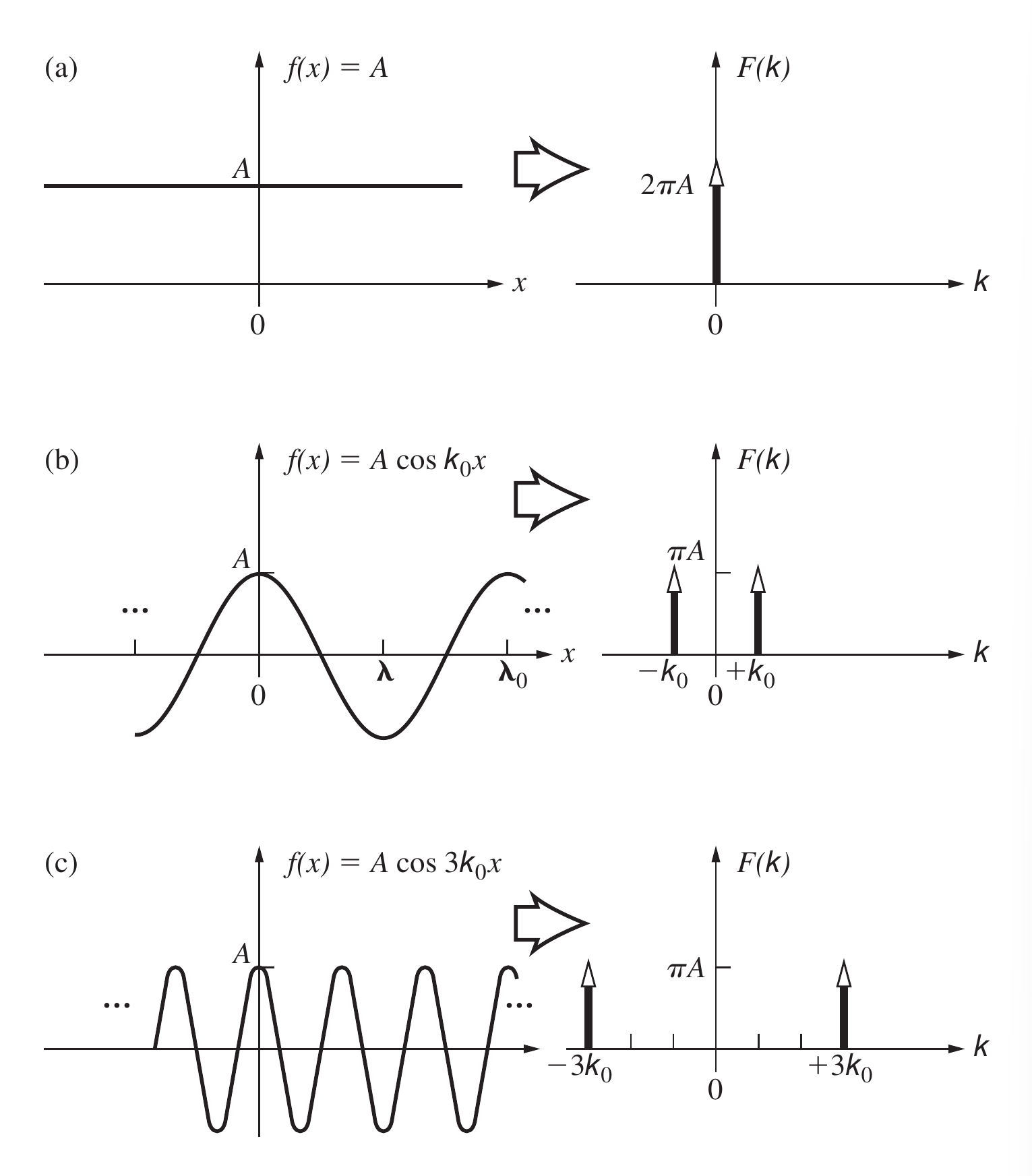
二维光学图像
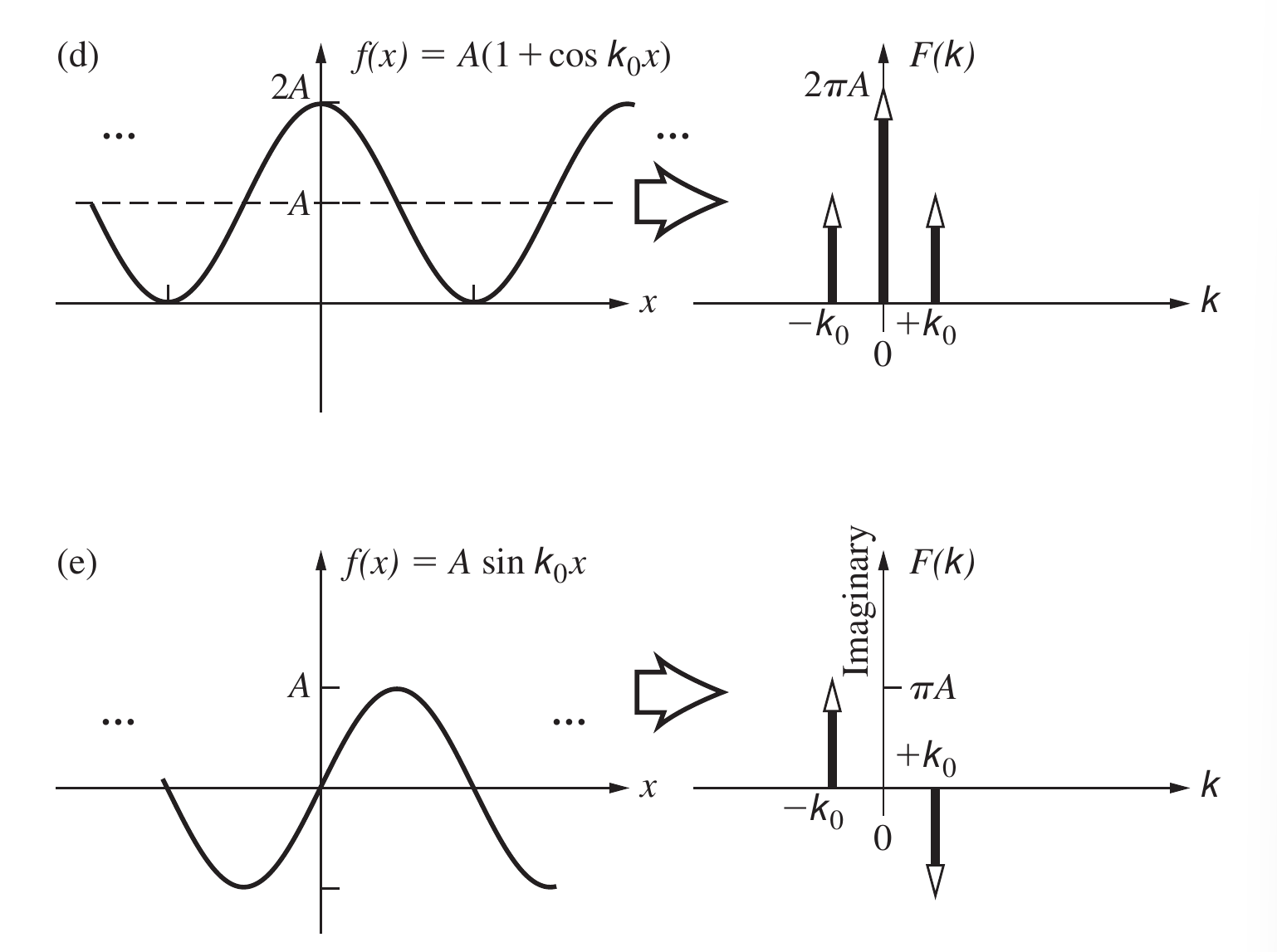
在光学中, 我们难以直接表达图像对应信号中的负数成分, 所以我们常常在信号中加入直流的成分使得信号总是能够落在中, 原来的振幅信号就被用的振幅来表示.
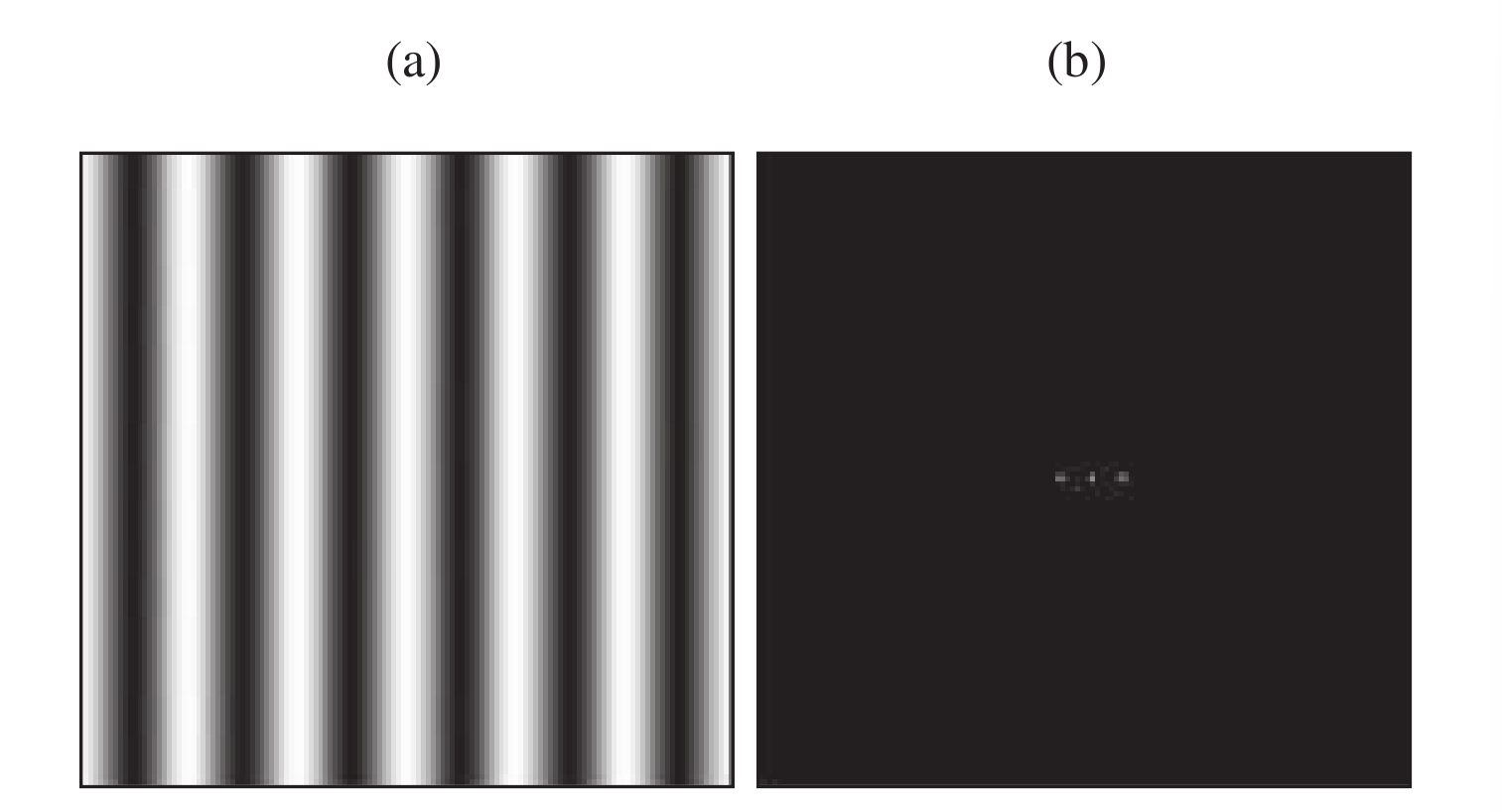
下图是一个余弦信号, 它的频谱信号中的三个光点就对应于上面图中的三个峰
 下面是不同的情况
下面是不同的情况
 上面展示的二维Fourier变换, 其中每个点或像素代表一个特定的Fourier频率分量. 中心的点代表直流项, 在物理图像系统中总是存在这样的分量. 它被两个点所包围, 这两个点代表了余弦波的频率信息. 像素的亮度代表了特定空间频率傅里叶分量的幅度.
上面展示的二维Fourier变换, 其中每个点或像素代表一个特定的Fourier频率分量. 中心的点代表直流项, 在物理图像系统中总是存在这样的分量. 它被两个点所包围, 这两个点代表了余弦波的频率信息. 像素的亮度代表了特定空间频率傅里叶分量的幅度.
在上面这种情况下, 弦函数的信号带是竖直的条状的, 因此Fourier像素沿着通过直流中心的垂直水平线展开. 频率域中的这三个像素与相关的亮度余弦波携带相同的信息;它们告诉我们在空间域中指定该信号所需知道的一切.
如果空间信号的波长发生变化, 变换像素之间的间距将以相反的方式变化;空间波长越短, 即空间频率越高, 像素之间的距离越远, 但模式始终关于零对称. 像素离变换中心越远, 其空间频率越高. 空间中的精细图案需要变换中的高频分量(远离中心的像素)
又由于几个函数之和的Fourier变换等于这些函数各自Fourier变换的和. 我们将上面图中不同频率的余弦信号相加, 就能生成了下图中复杂的带状图案.
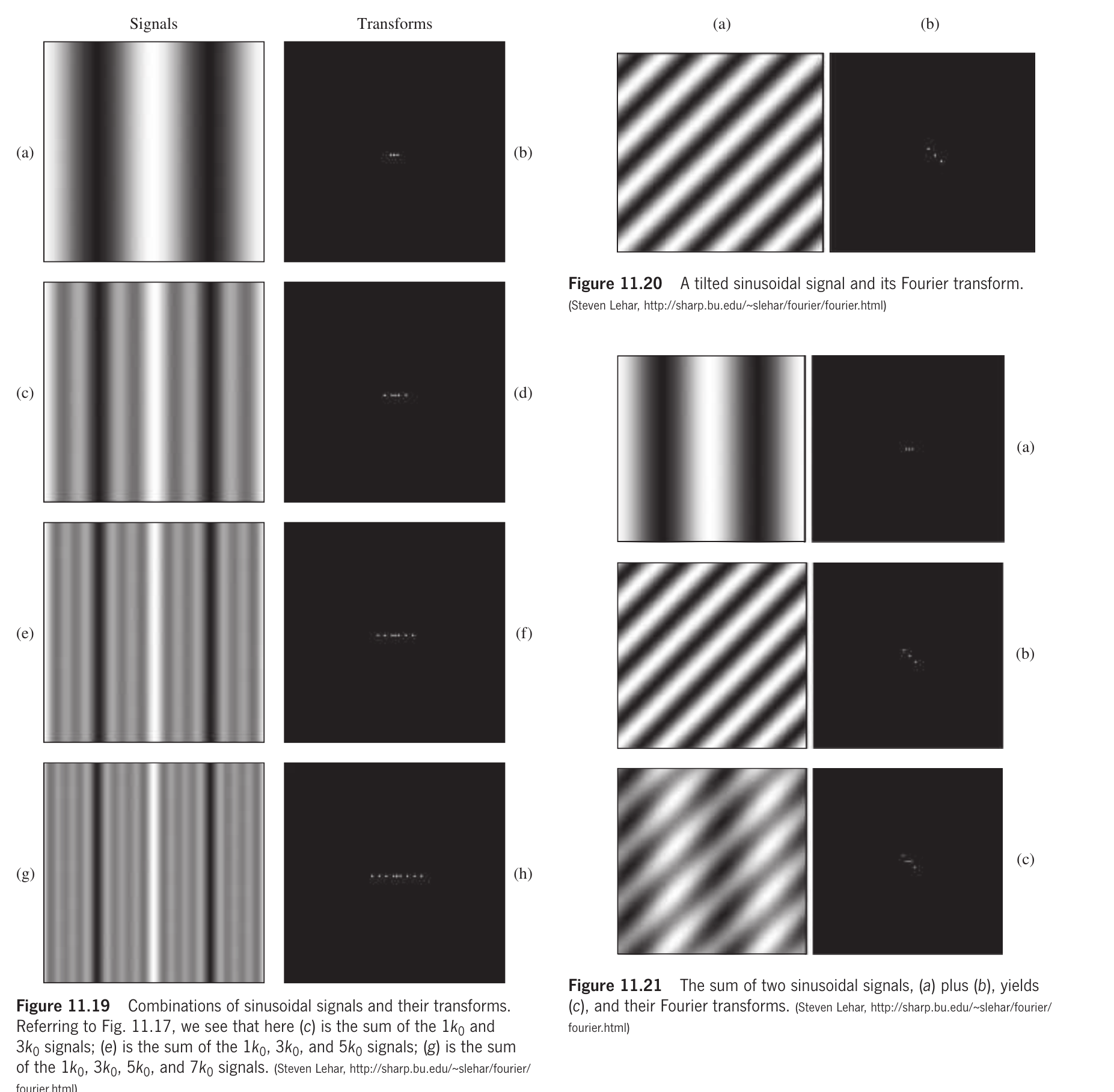
每个变换实际上是单个变换的累加结果. 虽然在图片上不太明显, 但随着中心条纹在连续信号中变得更亮、更窄, 其对应的直流分量(即信号的平均值)也在增加. 这一过程类似于多缝衍射现象, 其中随着更多贡献的增加, 主要极大值变得更细更高.
如果我们把余弦信号旋转一个任意角度, 信号的空间波长和幅度保持不变. 这个倾斜信号的Fourier变换(假设信号是无限的)与之前相同, 仍然是三个脉冲函数. 这些脉冲函数位于与信号带垂直的直线上, 并且与信号一样旋转了相同的角度. 在上述所有情况下, 如果我们对每个Fourier变换取逆变换, 我们就能重建原始的空间信号.
若把上面图中的倾斜信号与图中的最低频率信号相加, 生成图左侧的模式. 这个组合信号的Fourier变换是构成该信号的各个变换的和, 即三个水平脉冲点叠加在三个倾斜脉冲点上. 这展示了如何通过添加许多不同方向、涵盖广泛空间频率的余弦项来生成更复杂的图像.
Fraunhofer 衍射
光屏上一点接受到的电场振幅可以写成一个对衍射屏的积分
其中屏函数包含振幅衰减因子和相位改变因子两项
分析衍射屏上每一个面元在光屏上某点贡献的振幅, 可以看做是由一列沿着方向(即方向)传播的振幅为平面波贡献的(在远场条件下, 光屏接收到的光波才能被视为平面波;又因为光屏足够远, 尺度也远大于像小孔这样的衍射屏, 所以只要接受的位置确定, 衍射屏上的每一个面元产生的平面波都可以看作拥有一样的)
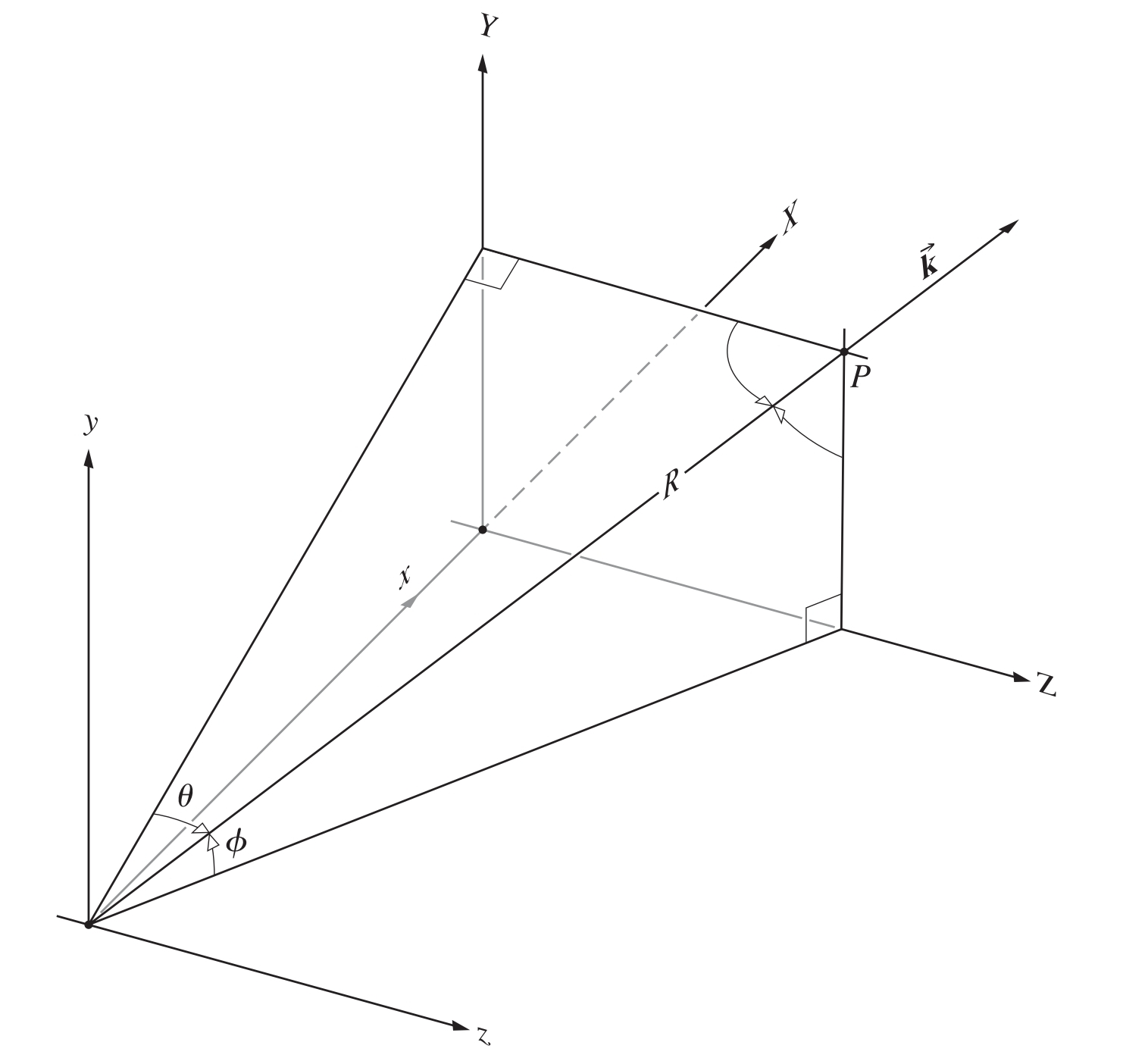 由上图中的几何关系, 我们可以定义角度空间频率为
由上图中的几何关系, 我们可以定义角度空间频率为
光屏上的每一个点都有一个对应一对空间频率, 由此衍射场就可以被写成
这个形式和上文中的二维Fourier变换中的形式是一致的, 所以可以被写成
这指出了Fraunhofer衍射的衍射场分布就是屏函数的Fourier变换
同理我们可以通过Fourier逆变换求出屏函数
从上文的Fourier变换的性质中我们知道, 信号的宽度越窄, 它的Fourier变换就越宽, 这在二维情况下也成立, 表现在衍射中就是衍射空越窄, 屏函数的信号宽度也越窄, 衍射光束和相应的条纹也就越宽
在实际情况下, 我们不可能在无穷远处放置屏幕来观察衍射图样. 通常, 我们会在一个有限距离处放置屏幕. 在这种情况下, 观察到的电场分布和理想的Fraunhofer衍射电场分布相比, 会有非常小的相位差异. 这是因为在有限距离处, 光波前还不能完全被看作平面波, 仍有一定的曲率, 导致相位的微小变化.
这个相位差异在大多数情况下并不显著, 尤其是对于我们实际观测的辐照度(光强)来说. 辐照度只与电场幅度的平方成正比, 而相位差异不影响电场幅度, 因此我们在有限距离处观察到的衍射图样在强度分布上与理想的Fraunhofer衍射几乎一致.
截止频率
截止频率
由于在频谱中靠近中心的是低频分量, 而远离中心的是高频分量;又因为一个透镜的线度是有限的, 它无法把超过它线度的高频分量作为波源传播下去, 所以透镜实质上是一个漏高频的低通滤波器, 它能通过的最高频率和c从衍射屏相对它发出平行光的最大衍射角的关系是 这个被称为此透镜的截止频率(cut-off frequency)
相对孔径和最小分辨距离
在计算截止频率时, 常与透镜的孔径和焦距有关, 在光源的线度远小于透镜的线度时, 近似地有
其中我们定义这个镜头的相对孔径为, 于是有镜头的最小分辨距离
注意, 这里的最小分辨距离是在相干光的条件下定义的(Abbe光学系统要求相干光), 在非相干的条件下, 有显微镜的最小分辨距离
由Airy斑确定, 其中, 可以看出这两种条件下最小分辨率都是差不多的