Light Dispersion

正常色散

光在介质中的传播速度$v$(或者说折射率$n=\frac{c}{v}$)随波长$\lambda$而异的现象称为色散

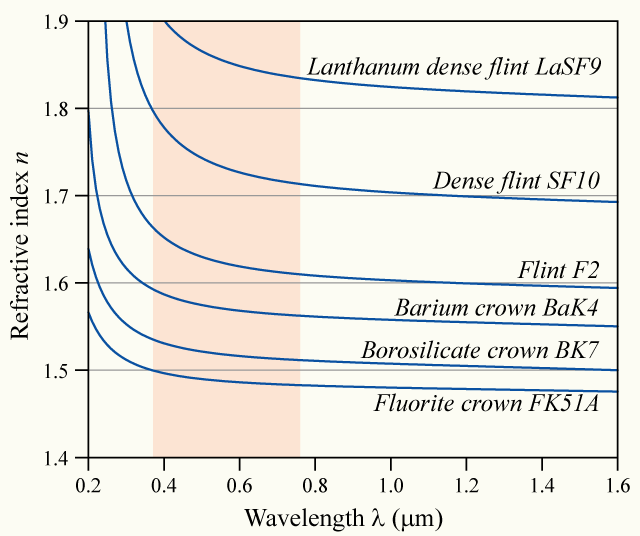
回忆三棱镜的色散作用，测量不同波长的光通过棱镜的偏转角，就可以算出棱镜材料的折射率$n$与波长$\lambda$之间的依赖关系曲线，即色散曲线. 实验表明，凡是在可见光范围内无色透明的介质，它们的色散曲线在形式上很相似，比如说$n$随着$\lambda$的增加而单调下降，且下降率在短波一端更大. 这种色散被称为正常色散 1836年Cauchy给出了一个正常色散的经验公式

$$n=A+\frac{B}{{\lambda }^2}+\frac{C}{{\lambda }^4}$$

当$\lambda$变化范围不大时，可以只取前两项

$$n=A+\frac{B}{{\lambda }^2}$$

反常色散

实验表明，在强烈吸收的波段，色散曲线与正常色散曲线有很大的不同. Wood在观察钠蒸汽的色散的时候，发现在钠的吸收线附近，水平光谱段被严重的扭曲和割断，这种现象叫做反常色散 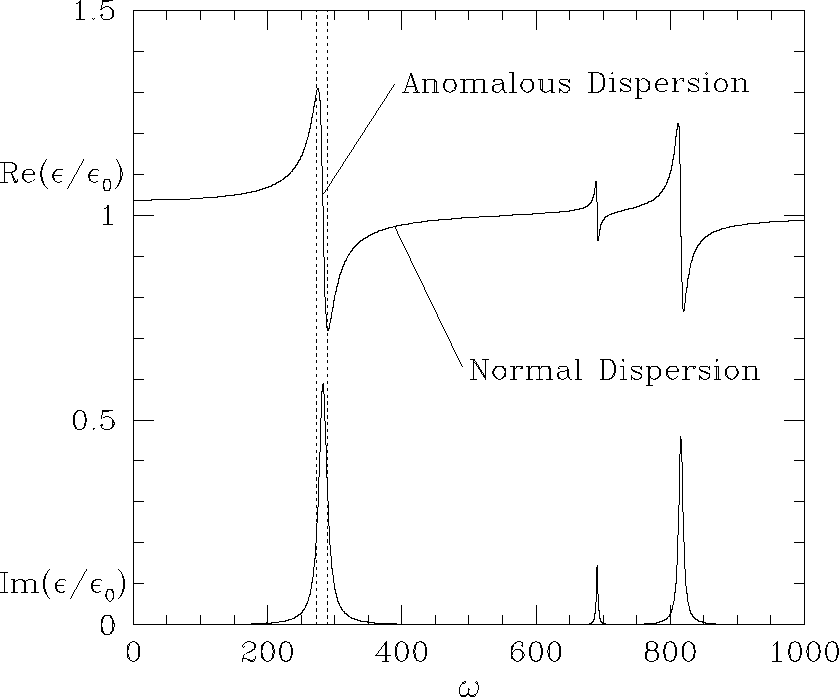反常色散的名称时历史上沿用下来的，其实任何物质在吸收线附近都有反常色散的现象，所以这种现象严格意义上不能算作“反常”

一种物质的全部色散曲线

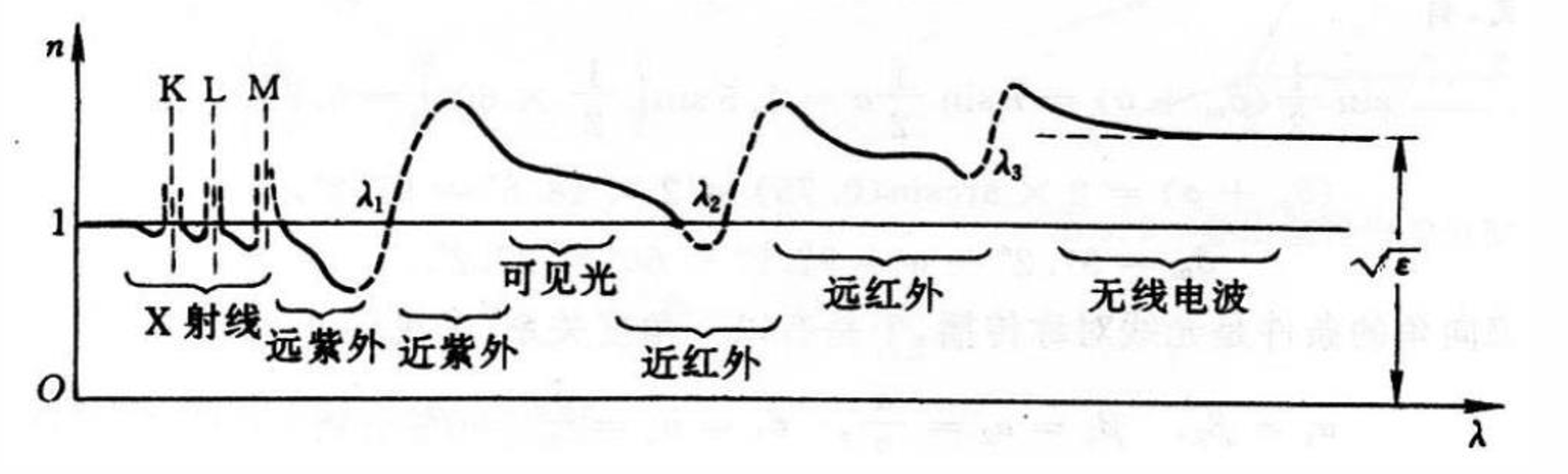在相邻的两个吸收带之间$n$随着$\lambda$单调下降，每次经过一个吸收带，$n$急剧增大. 总的趋势是曲线随着$\lambda$的增加而抬高

群速和相速

一般而言，当我们提及光在各向同性介质中的波速时，都指的是波面（等相位面）传播的速度，即相速（phase velocity），用$v_p$来表示. 在真空中所有波长的电磁波以同一相速$c$传播，在色散介质中只有理想的单色波具有单一的相速.

但是理想的单色波是不存在的，波列不会无限长. 一列有限长的波相当于许多单色波列的叠加，通常把由这样一群单色波组成的波列叫做波包（wave packet）. 当波包通过有色散的介质时，它的各个单色分量将以不同的相速前进，整个波包在向前传播的同时，其形状也会发生变化. 称波包中振幅最大的地方叫做它的中心，以波包中心为代表的前进速度叫做群速（group velocity）

在介质中，$f$不变，而$\lambda =\frac{c}{nf}$，设$\omega =2\pi f,k=\frac{2\pi }{\lambda }=\frac{2\pi nf}{c}$，我们有$v_p=\frac{c}{n}=\frac{\omega }{k}$，而通过Fourier变换，可以推导得

$$v_g=\frac{\mathrm{d}\omega }{\mathrm{d}k}$$

注意到$n=\frac{c}{v_p}=\frac{ck}{\omega }$，于是

$$\frac{\mathrm{d}n}{\mathrm{d}\omega }=\frac{c}{\omega }\frac{\mathrm{d}k}{\mathrm{d}\omega }-\frac{ck}{{\omega }^2}$$

也就是

$$\omega \frac{\mathrm{d}n}{\mathrm{d}\omega }=\frac{c}{v_g}-\frac{c}{v_p}$$

定义折射率$n=\frac{c}{v_p}$，群速折射率$n_g=\frac{c}{v_g}$，则有

$$\boxed{n_g=n-\lambda \frac{\mathrm{d}n}{\mathrm{d}\lambda }}$$

上式也说明了没有色散（$\frac{\mathrm{d}n}{\mathrm{d}\lambda }=0$）时，群速和相速没有区别.

除了根据用Huggens原理直接用折射率法测出得光在介质中得速度时相速度之外，大多数其他方法测出得其实是光的信号速度，也就是能量的传播速度. 而波包中振幅最大的地方也就是能量最集中的地方，所以可以认为我们一般测到的光速都是群速度

有些时候，相速度$v_p$是可以超过光速$c$的，但是波的信号速度总是小于$c$. 在正常色散区，波的信号速度就是其群速度，它总是小于$c$的；但是在反常色散区，群速度可以大于$c$，也可以是负值，但是这个时候群速度显然就不能代表信号速度了，实验证明，光传播信号的速度确无法大于光速$c$

色散本领

回忆光栅的色分辨原理