Optical Information

空间频率

通过Fourier 变换, 我们可以把一个二维图像变换到它的频谱, 并由此重构出一个相似的图像. 对于远场Fraunhofer衍射, 它的衍射图样就是屏函数$\mathcal{A}(y,z)$的Fourier变换, 而为了能在更近的距离观察到它的条纹, 我们会引入一个变换透镜来使衍射光线在更近的地方汇聚. 我们可以把这么一个装置整体看作为一个光学计算器, 它能够实时地计算Fourier变换.

考虑一列空间相干的平面波通过一个理想光栅, 光栅的屏函数如下, 其中$a$是光栅常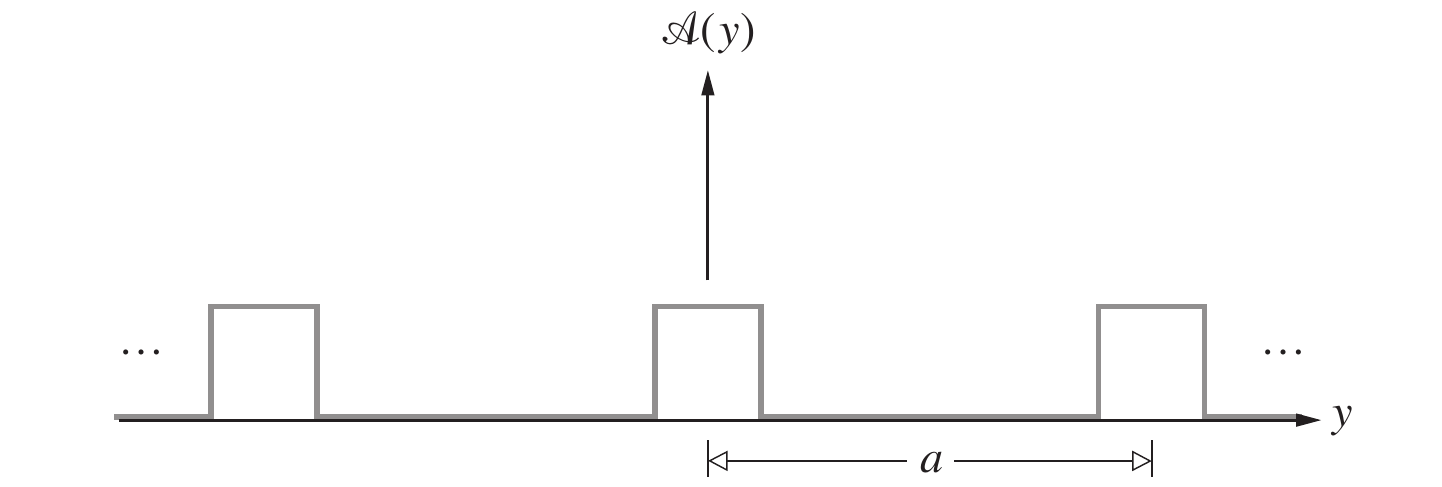数 平行光经过光栅后, 形成如下衍射条纹 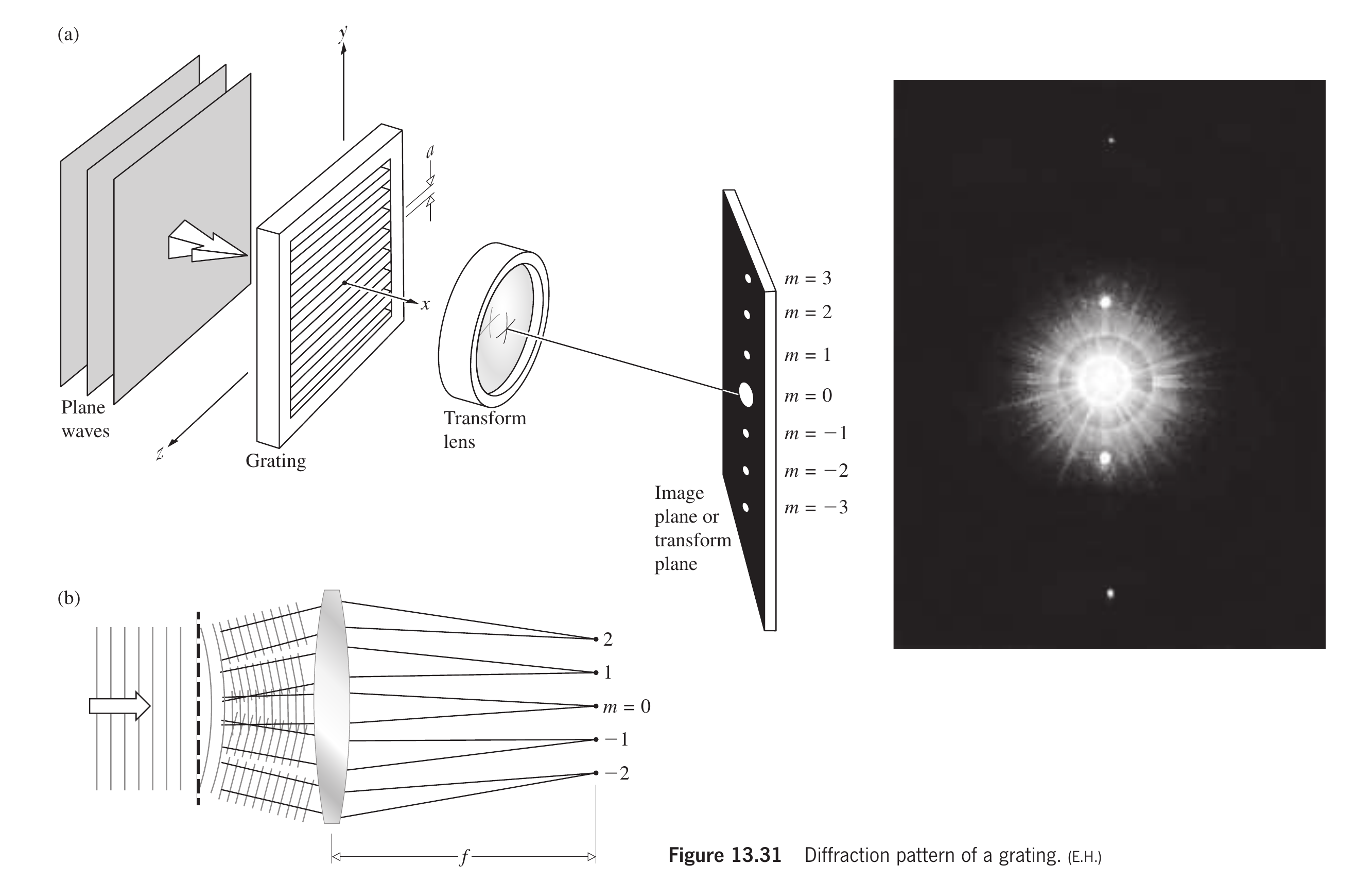其中中心亮条纹$(m=0)$代表的直流分量体现了一个零空间频率, 也就是一个由输入$\mathcal{A}(y)$的恒正性得到的偏移量.

当逐渐远离中心时, 由光栅公式

$$a\sin {\theta }_m=m\lambda$$

和Farunhofer衍射中的空间频率

$$k_y(m)=k\sin {\theta }_m⟹f_y(m)=\frac{1}{\lambda }\sin {\theta }_m$$

得到$m$级亮纹代表了空间频率为$\frac{1}{\lambda }\cdot \frac{m\lambda }{a}=\frac{m}{a}$的成分. 当$a$增大时, 每一个$m$都会代表更低的空间频率, 而频谱中低频成分集中在中心, 所以衍射光点也会更加靠近中心

总结

衍射图案中的每一个光点都代表了一种空间频率, 且空间频率的大小和它离中心光轴的距离成正比

Abbe成像理论

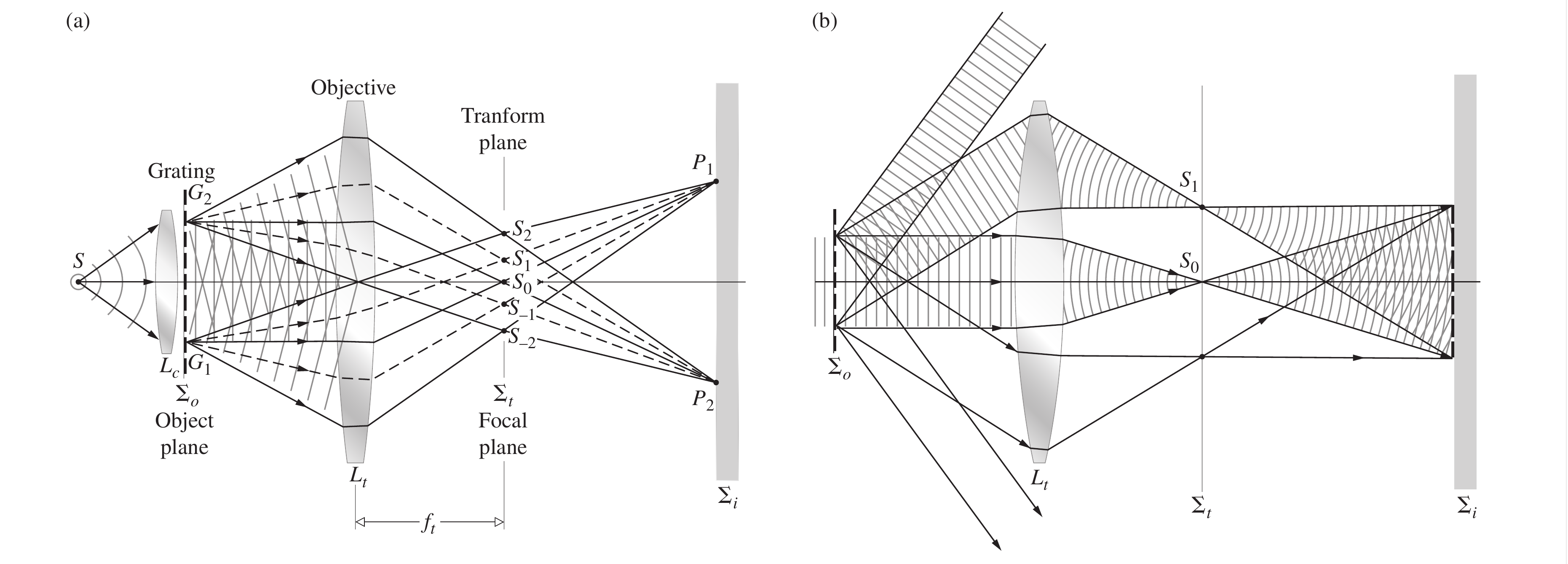
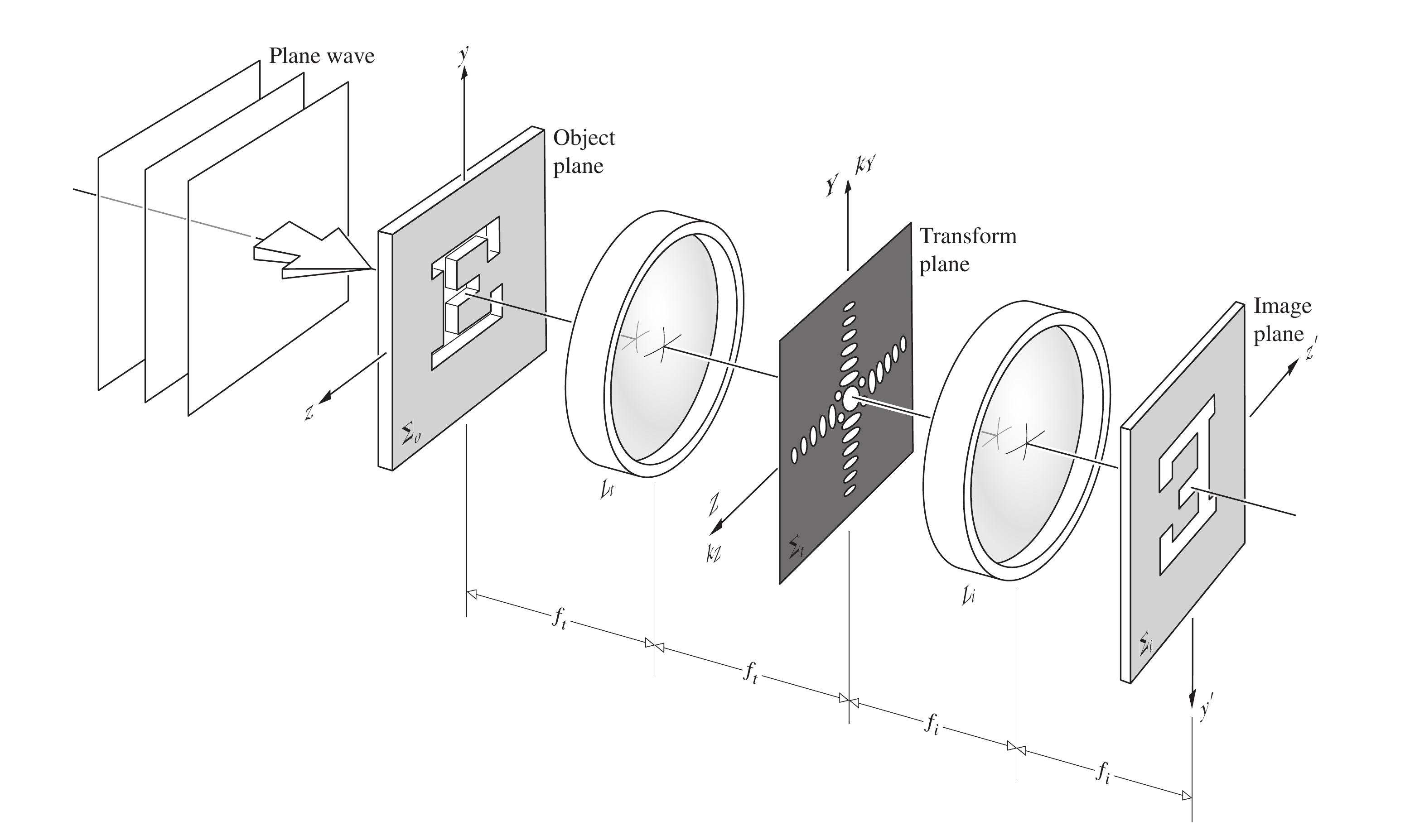
考虑上图的光学系统$(a)$, 准直透镜($L_c$)发射出平面单色波, 这些波前被光栅衍射. 衍射后的波前变得扭曲, 我们将其解析为一组新的平面波, 每个波对应一个特定的级数$m=0,\pm 1,\pm 2,...$或空间频率, 并且沿特定方向传播, 就如$(b)$中所示的那样

物镜$(L_t)$是变换透镜, 在${\Sigma }_t$（也就是$L_t$的后焦面）上形成Fraunhofer衍射图样. 这些波通过${\Sigma }_t$后到达像平面${\Sigma }_i$后将重叠并相互干涉, 形成光栅的倒立图像（例如坐标的$G_1,G_2$分别成像在$P_1,P_2$）.

在这个光学系统中两个值得关注的图样, 一个是源$S$所在平面的共轭${\Sigma }_t$上的由Fourier变换形成的图样, 另一个是物平面的共轭${\Sigma }_i$上的图像.

下图是采取平面单色光源照明一个单缝时物平面和上述两个平面上的振幅分布 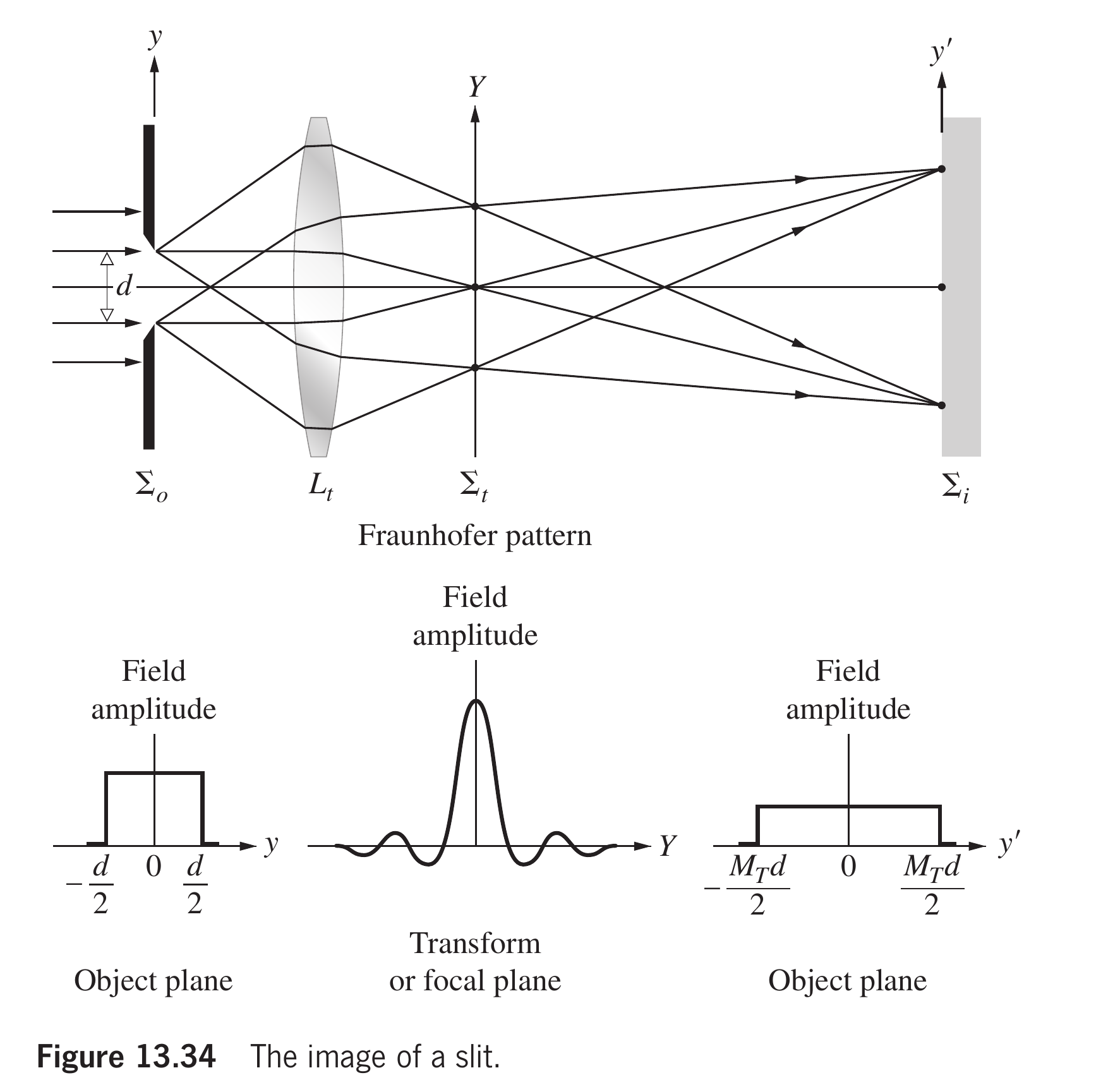这些系统最初是在$1873$年由Ernst Abbe$(1840-1905)$提出的. 当时他的兴趣集中在显微镜理论的研究上. 如果我们把$L_t$视为显微镜的物镜, 那么它与上述讨论的联系就很明显了. 此外, 如果将光栅替换为一块薄薄的半透明材料（即待检测的样本）, 并用来自小光源和聚光器的光线照亮, 这个系统显然与显微镜非常相似.

Carl Zeiss$(1816-1888)$在19世纪中叶经营着Jena的一间小型显微镜工厂, 他认识到当时显微镜发展过程中试错法的局限性. $1866$年, 他邀请了当时在Jena大学任讲师的Ernst Abbe, 共同探索一种更科学的显微镜设计方法. Abbe通过实验发现, 即使入射光锥只占物镜的一小部分, 较大的孔径也能带来更高的分辨率, 周围的“暗空间”似乎对成像有所贡献. 因此, 他提出了一种观点: 在镜头边缘发生的衍射过程（对于点光源产生Airy图案）并不像非相干照明的望远镜物镜那样起作用. 大小与$l$相当的标本显然是将光线散射到显微镜物镜的“暗空间”中. 观察图$b$, 如果物镜的孔径不足以收集所有衍射光, 则图像并不完全对应于原物体. 相反, 它与一个虚构的物体有关, 其完整的衍射图案与$L_t$收集的图案相匹配.

实际上, 除非物镜具有无限大的孔径, 否则它作为一个低通滤波器, 会拒绝超过某一特定值的空间频率（也就是截止频率）, 并允许所有低于该值的频率通过（前者是那些超出镜头物理边界的频率）. 因此, 所有实际镜头系统在相干照明下复制实际物体的高空间频率内容的能力都将受限

在下面的系统中, 我们将解释Abbe成像原理将平行相干光照明透镜成像分成了两步

1. 物平面发生Fraunhofer衍射, 在透镜像方焦面上形成的衍射图样是物平面的空间频谱
2. 频谱面上的各衍射斑发出的次波在像平面上干涉, 形成的图样即为像

空间滤波和4F系统

在Abbe光学系统中, 如果去除准直透镜$L_c$, 那么在$L_t$的左焦平面${\Sigma }_0$上发射的光将会在无穷远处汇聚, 这时候我们也可以类似地引入成像透镜$L_i$使得

• $L_t$让衍射图样成在有限远处
• $L_i$让物的像成在有限远处 事实上, 这个成像透镜也实现了一个Fourier变换, 可以把它的作用看作把${\Sigma }_t$上的衍射图样再次作逆Fourier变换呈现到${\Sigma }_i$上

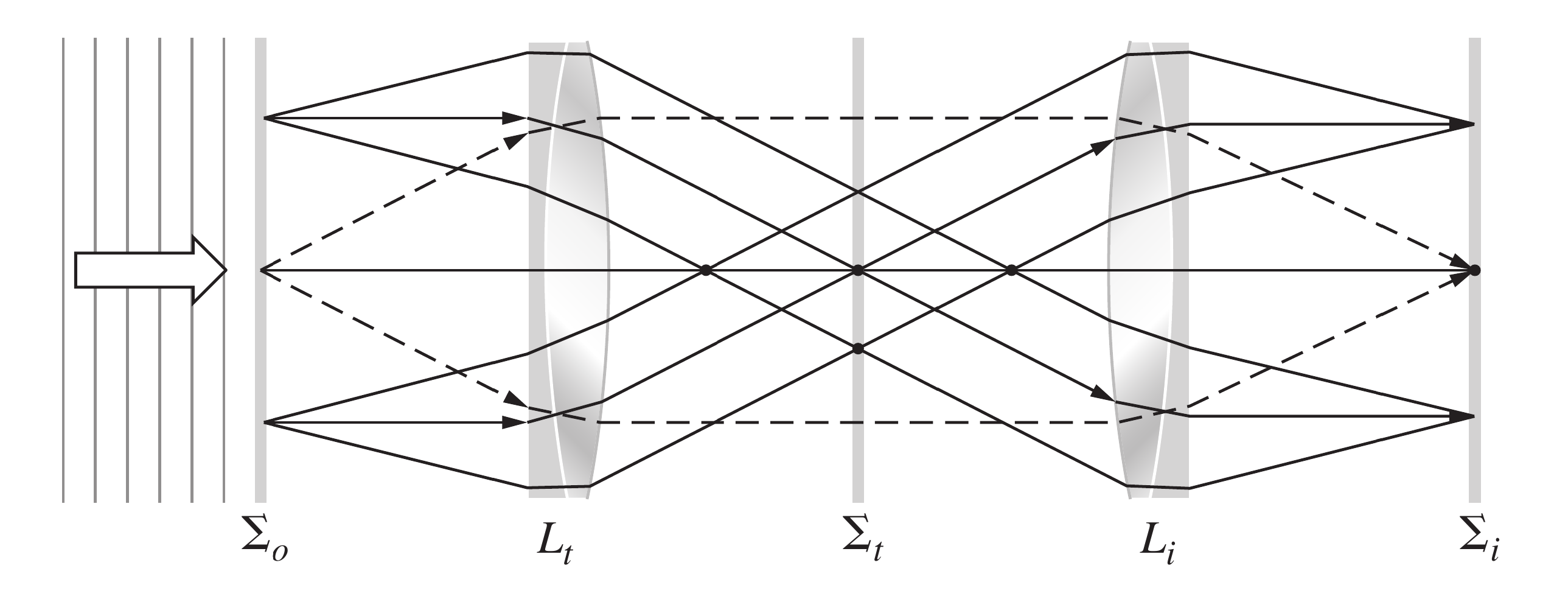如下图, 我们常常取$f_t=f_i$, 这个光学系统被称为4F系统 我们可以通过在${\Sigma }_t$上设置遮光屏来控制对应频率分量的通过性, 从而实现操作图像的目的, 这种操作也被称为空间滤波

振幅分布的计算

如果的变换屏的屏函数$t(x,y)\equiv 1$, 整个系统就是对物的波前${\tilde{U}}_o(x,y)$作了两次Fourier变换, 数学推导和物理分析都告诉我们

$${\tilde{U}}_i(x^{\prime },y^{\prime })=\mathcal{F}\left\{\mathcal{F}\left\{{\tilde{U}}_0(x,y)\right\}\right\}\propto \tilde{U}(-x^{\prime },-y^{\prime })$$

这说明连续两次的Fourier变换不改变函数的形式, 只是自变量的符号改变, 也就是图像倒置. 所以这个过程也可以看作为一次Fourier变换, 然后再一次逆Fourier变换并倒置图像

但是在有滤波器的情况下, 在频谱面上有

$${\tilde{U}}_{t2}=\tilde{t}\cdot {\tilde{U}}_{t1}$$

这时候经过第二次Fourier变换后, 函数形式不再是复原加图像倒置, 但是我们仍然可以对${\tilde{U}}_{t2}$作Fourier逆变换, 然后倒置图像, 由此来代替第二次Fourier变换的运算.

正弦光栅滤波器

设

$$\tilde{t}(k_x,k_y)=t_0+t_1\cos (2\pi f_0\xi )$$

则整个变换过程为

1. ${\tilde{U}}_{t1}(\xi ,\eta )=\mathcal{F}\left\{{\tilde{U}}_o(x,y)\right\}$
2. ${\tilde{U}}_{t2}(\xi ,\eta )=\tilde{t}(\xi ,\eta ){\tilde{U}}_{t1}(\xi ,\eta )$
3. ${\tilde{U}}_i(x^{\prime },y^{\prime })=\mathcal{F}\left\{{\tilde{U}}_{t2}(\xi ,\eta )\right\}$

其中最后一步可以进一步写成(用$\ast$表示卷积)

$${\tilde{U}}_i(x^{\prime },y^{\prime })=\mathcal{F}\left\{\tilde{t}(\xi ,\eta ){\tilde{U}}_{t1}(\xi ,\eta )\right\}=\mathcal{F}\left\{\tilde{t}(\xi ,\eta )\right\}\ast \mathcal{F}\left\{{\tilde{U}}_{t1}(\xi ,\eta )\right\}$$

利用上面的结论, 就有

$$\boxed{{\tilde{U}}_i(x^{\prime },y^{\prime })\propto \mathcal{F}\left\{\tilde{t}(\xi ,\eta )\right\}\ast {\tilde{U}}_o(-x^{\prime },-y^{\prime })}$$

考虑正弦光栅的情况

$$\begin{array}{rl}\mathcal{F}\left\{\tilde{t}(\xi ,\eta )\right\}& =\mathcal{F}\left\{t_0+t_1\cos (2\pi f_0\xi )\right\}\\ & =t_0\delta (f_{\xi })+\frac{t_1}{2}\left[\delta (f_{\xi }-f_0)+\delta (f_{\xi }+f_0)\right]\end{array}$$

于是

$$\begin{array}{rl}{\tilde{U}}_i(x^{\prime },y^{\prime })& \propto \left\{t_0\delta (f_{\xi })+\frac{t_1}{2}\left[\delta (f_{\xi }-f_0)+\delta (f_{\xi }+f_0)\right]\right\}\ast {\tilde{U}}_o(-x^{\prime },-y^{\prime })\\ & =\left\{t_0\delta (\frac{x^{\prime }}{\lambda F})+\frac{t_1}{2}\left[\delta (\frac{x^{\prime }}{\lambda F}-f_0)+\delta (\frac{x^{\prime }}{\lambda F}+f_0)\right]\right\}\ast {\tilde{U}}_o(-x^{\prime },-y^{\prime })\\ & \propto \left\{t_0\delta (x^{\prime })+\frac{t_1}{2}\left[\delta (x^{\prime }-\lambda F{f}_0)+\delta (x^{\prime }+\lambda F{f}_0)\right]\right\}\ast {\tilde{U}}_o(-x^{\prime },-y^{\prime })\\ & =t_0{\tilde{U}}_o(-x^{\prime },-y^{\prime })+\frac{t_1}{2}\left[{\tilde{U}}_o(\lambda F{f}_0-x^{\prime },-y^{\prime })+{\tilde{U}}_o(-\lambda F{f}_0-x^{\prime },-y^{\prime })\right]\end{array}$$

最后三项分别表示$0$级像、$+1$级像和$-1$级像