Fraunhofer Diffraction

形成Fraunhofer衍射场的条件

远场条件

接收屏幕应该放得足够远, 由电磁波的远场条件知道接收屏和衍射屏之间的距离$z$需要满足

$$z\gg \frac{a^2}{\lambda }$$

其中$a$为衍射屏的线度, 可取为孔径大小

傍轴条件

接收屏幕上能形成Fraunhofer衍射图样的几何限度$\rho$也需要满足电磁波的傍轴条件, 也就是

$$\rho \ll z$$

实验现象

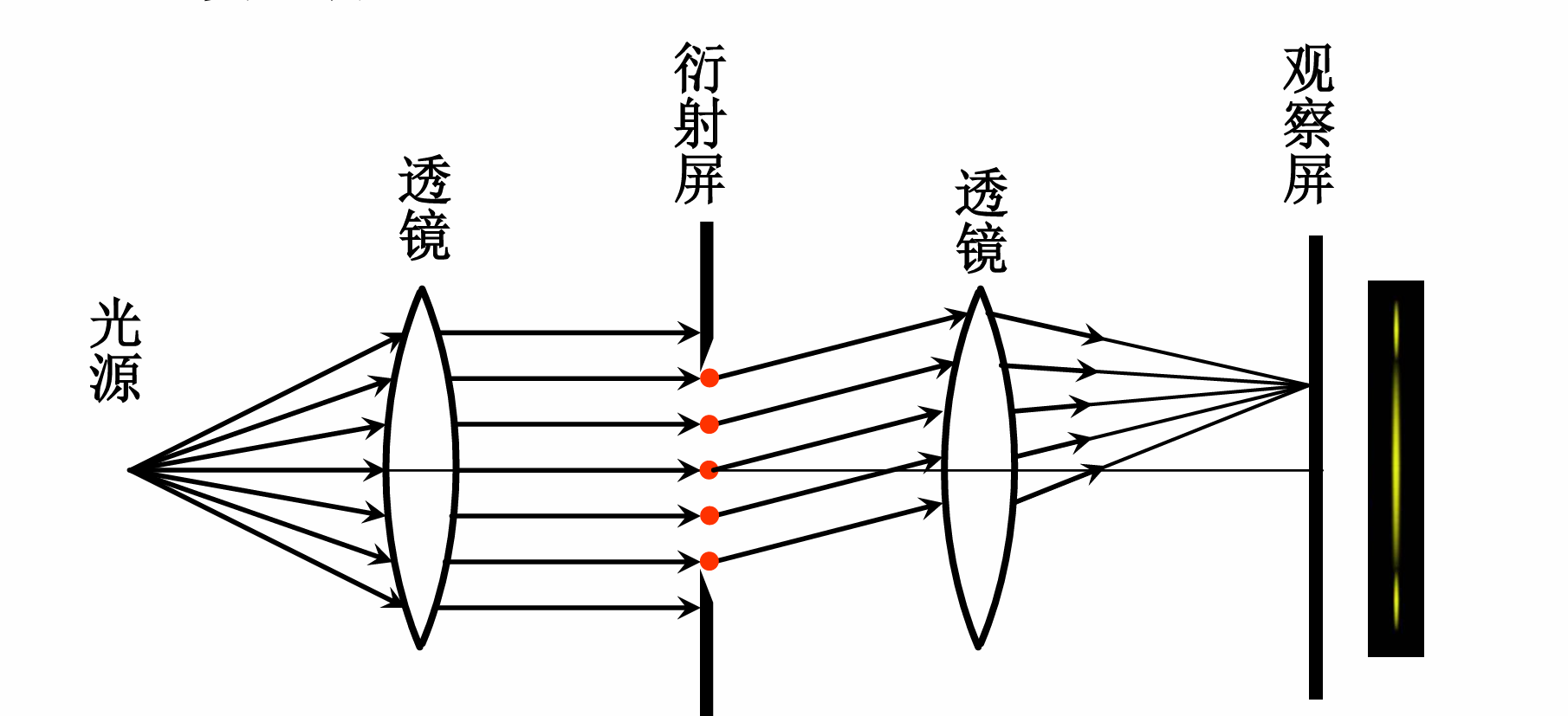一系列亮斑. 中心为亮斑, 亮度大于两侧的亮斑. 中心亮斑宽度是两侧的二倍, 亮斑的宽度随狭缝的变窄而展宽

单缝衍射

矢量图示

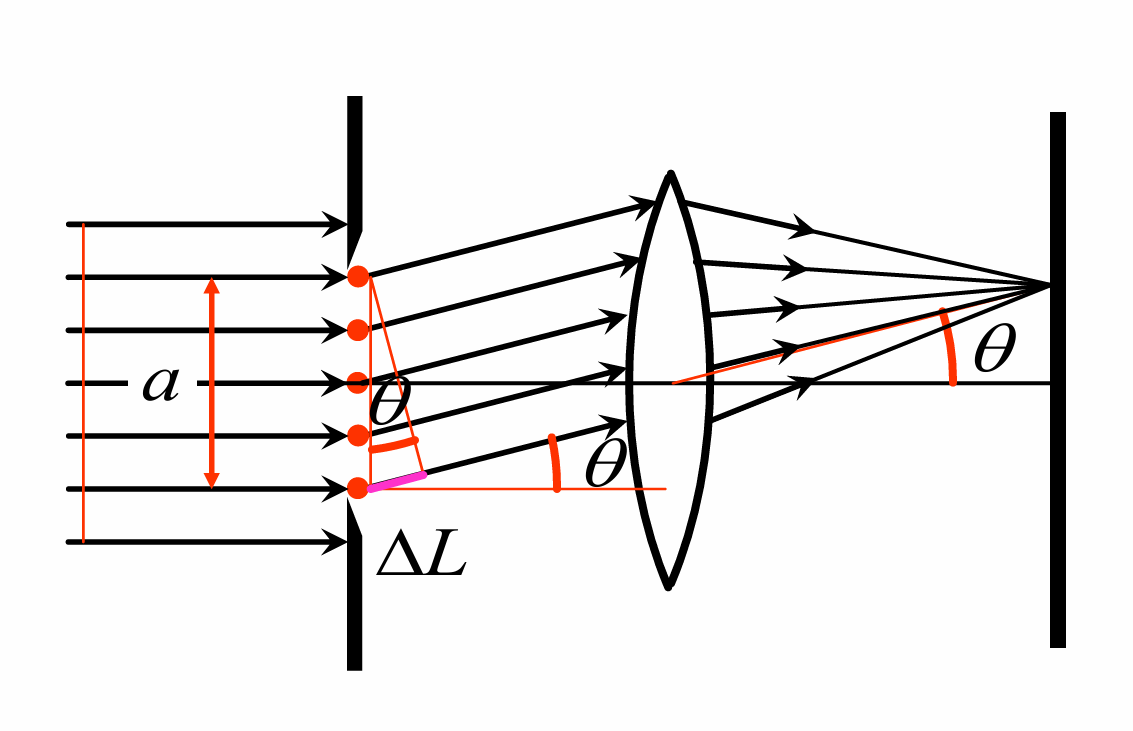用矢量图解法来分析屏上一点$P(\theta )$的振幅, 该点对应的光程差为

$$\Delta L=a\sin \theta$$

对应的相位差为

$$\Delta \varphi =\frac{\Delta L}{\lambda }\cdot 2\pi =\frac{2\pi a}{\lambda }\sin \theta$$

下图中的(b)和(c)(d)展现了$\Delta \varphi =0$和$\Delta \varphi =\pi$的情况, 前者振幅矢量均同向, 合成的振幅最大；后者振幅矢量会形成一个半圆, 合成的振幅大小为这个半圆的直径

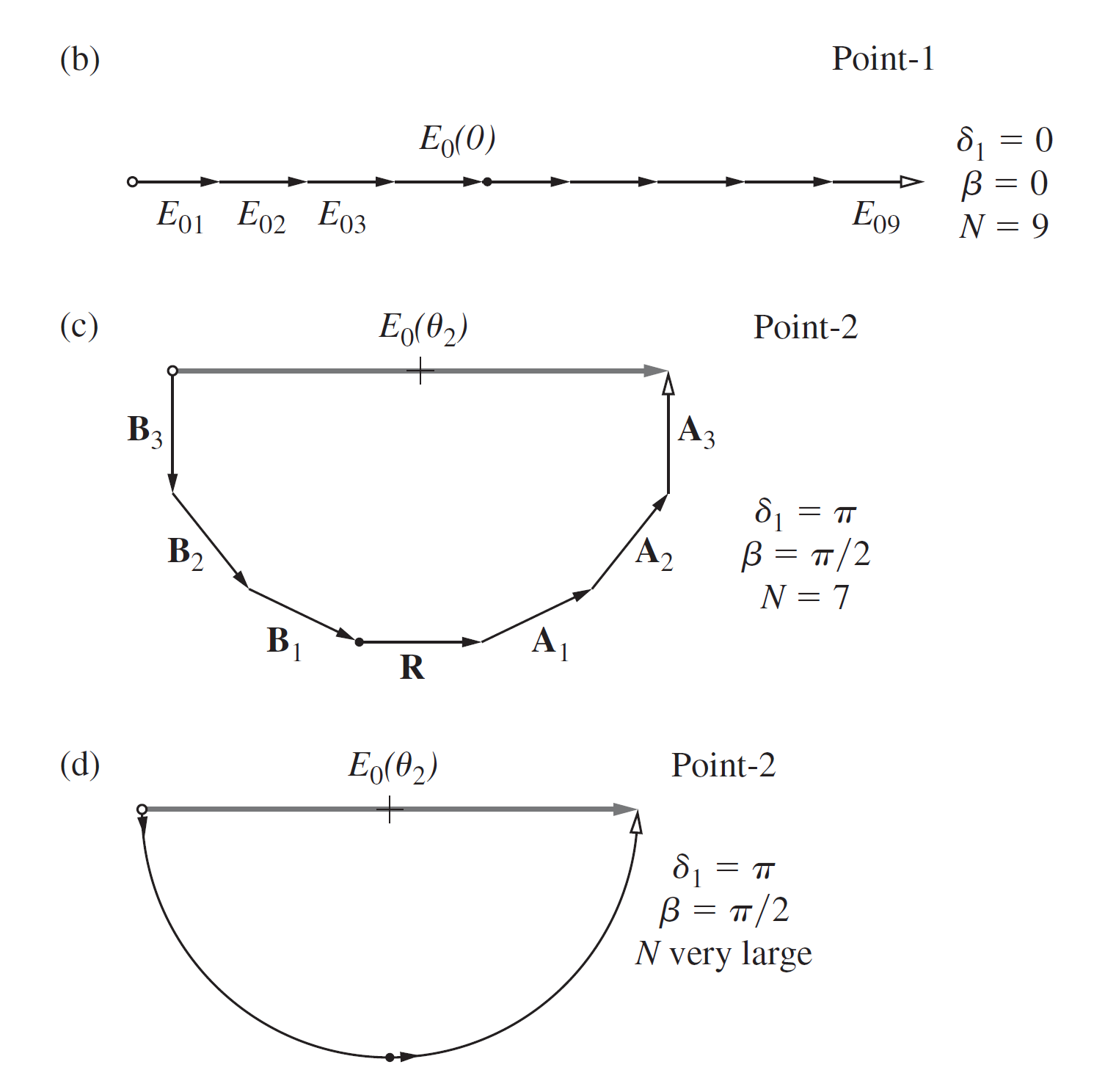再考虑$\Delta \varphi =2k\pi$的点, 它们的振幅矢量合成为一个完整的圆, 对应的振幅大小为零, 相应的$P$点为暗点. 这和两束光干涉的情况完全相反, 原因在于双缝干涉是离散的两束光波的合成, 而在衍射的情况下有无数连续的光束参与了合成

需要注意的是, 当$k$不断增大的时候, 振幅曲线的半径因为光的衰减会越来越多, 故对$\Delta \varphi =(2k+1)\pi ,k\ge 1$也就是$\Delta L=(k+\frac{1}{2})$的点来说, 虽然都是亮点, 但随着$k$的增大, 亮度会越来越低

上面排除了 $k=0$的情况, 这是因为

由于$\Delta L=0$的时候是最亮的点, 而$\Delta L=\lambda$的时候是第一个暗点, 所以当$\Delta L=\frac{\lambda }{2}$的时候其亮度处于二者之间, 不能算作暗点；但是对于$k\ge 1$的情况来说, 由于其两侧光程差为$\lambda$整数倍的点都是暗点, 故视其为亮点

定量分析

考虑$k$级暗纹

$$\Delta L=a\sin {\theta }_k=k\lambda ⟹\sin {\theta }_k=k\frac{\lambda }{a}$$

设$x$为定义在屏上的坐标, 则

$$x_k=f\tan {\theta }_k$$

其中$k=1,2,3,\dots$ 如果${\theta }_k\to 0$, 则有

$$|x_k|\approx fk\frac{\lambda }{a}=k\frac{\lambda }{a}f$$

对于$k$级亮纹, 类似地有

$$\sin {\theta }_k=\left(k+\frac{1}{2}\right)\frac{\lambda }{a}$$

其中$k=1,2,3,\dots$ 如果${\theta }_k\to 0$, 则有

$$|x_k|=\left(k+\frac{1}{2}\right)\frac{\lambda }{a}f$$

特别地, $0$级亮条纹在$x=0$的位置

条纹宽度

定义$k$级亮纹的角宽度为$\Delta {\theta }_k=\frac{\lambda }{a}$, 其中$k\ne 0$. 当$k=0$时, 定义$\Delta {\theta }_0={\theta }_{+1}-{\theta }_{-1}=2\frac{\lambda }{a}$

光斑的几何宽度$\Delta x_k=f\Delta {\theta }_k$, 几何直径$D_k=2f\Delta {\theta }_k$

单缝衍射因子

定义$\beta =\frac{\pi a}{\lambda }\sin \theta$（即$\theta$处相位差的一半）, 通过解Fresnel积分可以得到光强$I$关于$\beta$的分布

$$\frac{I(\theta )}{I(0)}={\left(\frac{\sin \beta }{\beta }\right)}^2$$

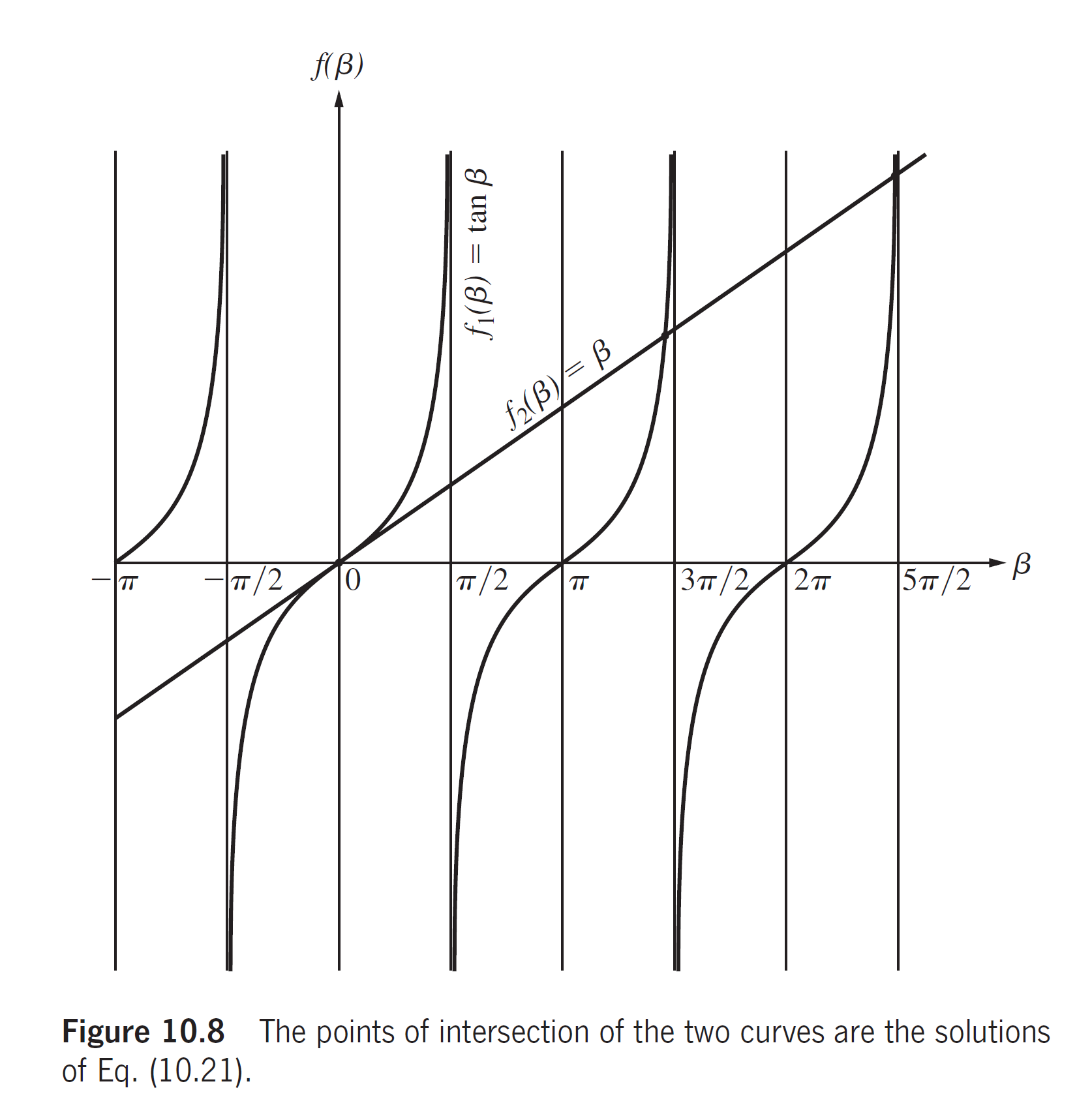解得$I(\theta )$的极大值满足$\beta =\tan \beta$ 可以近似为极大值出现在$\beta =\pm \left(k+\frac{1}{2}\right)\pi$处, 作$I\sim \beta$图像

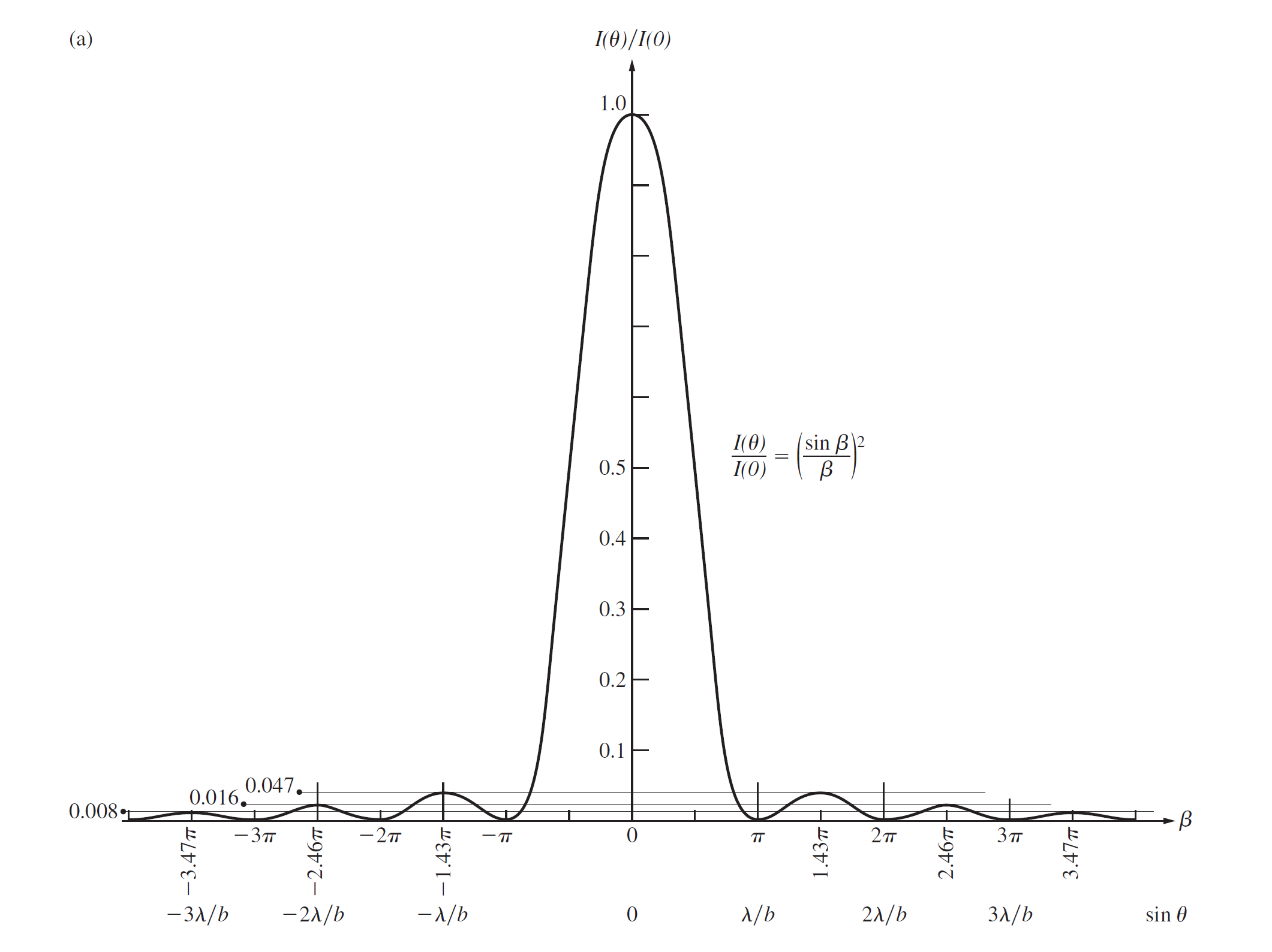
矩孔衍射的强度公式

光程差

$$\Delta L=-(x\sin {\theta }_1+y\sin {\theta }_2)$$

有

$$I({\theta }_1,{\theta }_2)=I_0{\left(\frac{\sin \alpha }{\alpha }\right)}^2{\left(\frac{\sin \beta }{\beta }\right)}^2$$

衍射反比关系

将角宽度公式$\Delta {\theta }_k=\Delta \theta =\frac{\lambda }{a}$变形, 有

$$\Delta \theta \cdot a=\lambda$$

这个反比和空间相干性的反比公式相似, 有如下意义

• 当$a$足够大时, $\Delta \theta$足够小, 对应于几何光学极限
• 参与干涉的波源数目越多, 出现干涉极大的条件越苛刻, 能量也越集中在某个特定的方向上
• 说明衍射具有放大作用, 可以用于测量单缝或细丝的宽度或直径

斜入射情形

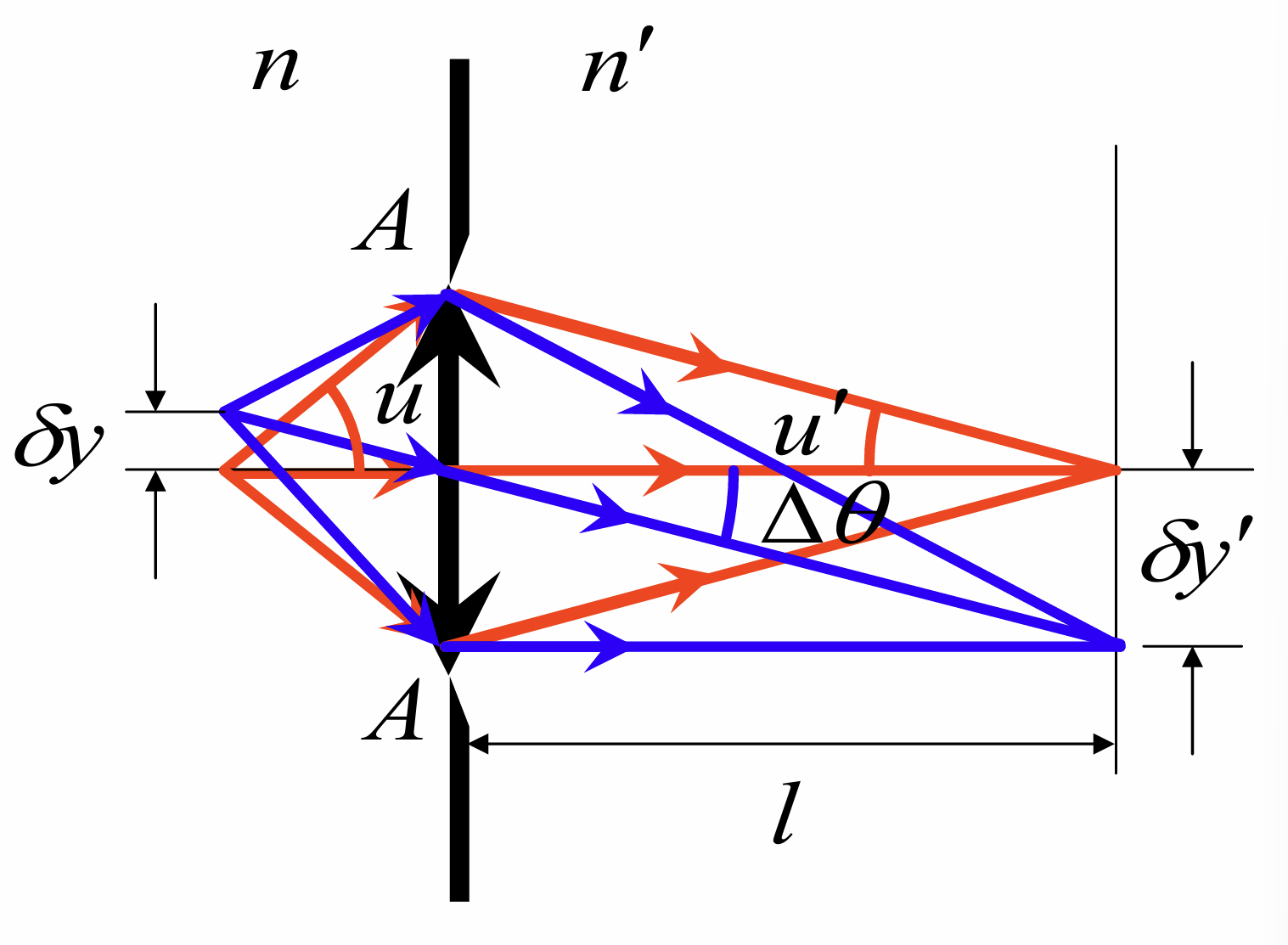
当平行光以${\theta }_0$角斜入射在宽度为$a$的单缝上时, 考虑光屏上角位置为$\theta$的点, 其光程差由经过单缝前后的两段路径分别贡献

$$\Delta L=\Delta L_0+\Delta L_1=-a\sin {\theta }_0+a\sin \theta =a\left(\sin \theta -\sin {\theta }_0\right)$$

这时候

1. 强度公式基本不变

$$I(\theta )=I(0)\left(\frac{\sin \alpha }{\alpha }\right)$$

只需要我们修正$\alpha$的定义为

$$\alpha =\frac{\pi a}{\lambda }(\sin \theta -\sin {\theta }_0)$$

2. 所以零级中心的位置仍然在几何光学像点处$\theta ={\theta }_0$, 而对于$k$级亮纹则有

$$\sin {\theta }_k-\sin {\theta }_0=\left(k+\frac{1}{2}\right)\frac{\lambda }{a}⟹\sin {\theta }_k=\sin {\theta }_0+\left(k+\frac{1}{2}\right)\frac{\lambda }{a}$$

3. 于是可以计算$k$级亮纹的角宽度（注意由于${\theta }_0$的存在我们无法假设$\theta \to 0$）

$$\frac{\lambda }{a}=\Delta (\sin {\theta }_k)=\cos {\theta }_k\Delta {\theta }_k⟹\Delta {\theta }_k=\frac{\lambda }{a\cos {\theta }_k}(k\ne 0)$$

特别地当$k=0$时, $\Delta {\theta }_0=\frac{2\lambda }{a\cos {\theta }_0}$, 其对于的半角宽就是$\frac{\lambda }{a\cos {\theta }_0}$

如果衍射屏前后两侧为不同介质, 设前场照明空间折射率为$n_1$, 后场衍射空间折射率为$n_2$, 则光程差变为$\Delta L=a(n_2\sin \theta -n_1\sin {\theta }_0)$, 从而有强度公式

$$I(\theta )=I(0)\left(\frac{\sin \alpha }{\alpha }\right),\alpha =\frac{\pi a}{{\lambda }_0}(n_2\sin \theta -n_1\sin {\theta }_0)$$

其中${\lambda }_0$表示衍射光在真空中的波长, 注意这里零级亮纹的位置${\theta }_0^{\prime }$需要满足

$$\alpha =0⟹n_2\sin {\theta }_0^{\prime }-n_1\sin {\theta }_0=0$$

即${\theta }_0^{\prime }$为斜入射光源通过衍射屏后的折射角, 而其他级亮条纹的位置为

$$n_2\sin {\theta }_k-n_1\sin {\theta }_0=\left(k+\frac{1}{2}\right)\frac{{\lambda }_0}{a}⟹\sin {\theta }_k=\frac{n_1}{n_2}\sin {\theta }_0+\left(k+\frac{1}{2}\right)\frac{{\lambda }_0}{n_{2}a}$$

它们的角宽度

$$\Delta {\theta }_k=\frac{{\lambda }_0}{n_{2}a\cos {\theta }_k}(k\ne 0)$$

特别地对于零级条纹, 其角宽度

$$\Delta {\theta }_0^{\prime }=\frac{2{\lambda }_0}{n_{2}a\cos {\theta }_0^{\prime }}=\frac{2{\lambda }_0}{a\sqrt{n_2^2-n_1^2{\sin }^2{\theta }_0}}$$

只有它半角宽才和其他的条纹有一样的形式, 即$\frac{{\lambda }_0}{a\sqrt{n_2^2-n_1^2{\sin }^2{\theta }_0}}$

光学仪器的分辨本领

Frauhofer圆孔衍射

在极坐标系下, 光程差为

$$\Delta L=-r\cos \phi \sin \theta$$

于是

$$\tilde{U}(\theta )=c\underset{0}{\overset{a}{\int }}\underset{0}{\overset{2\pi }{\int }}{e}^{-ikr\cos \phi \sin \theta }r\mathrm{d}r\mathrm{d}\phi =c\frac{2J_1(\alpha )}{\alpha }$$

得到

$$I(\theta )=I_0{\left(\frac{2J_1(\alpha )}{\alpha }\right)}^2,\alpha =\frac{\pi a}{\lambda }\sin \theta$$

可以解得对应的主极大半角宽

$$\Delta {\theta }_0=0.61\frac{\lambda }{a}=1.22\frac{\lambda }{D}$$

这个主极大的光斑被称为Airy斑, 其中$D$为衍射孔的直径

相机的光圈数

相机的光圈数定义为镜头焦距和最大光圈直径的比值, 即$\frac{f}{D}$. 例如, 如果镜头的最大光圈直径是$10$mm,焦距是$50$mm, 那么光圈数就是$50/10=5$, 通常记为$f/5$

光圈数越小, 表示光圈越大, 进光量越多. 光圈数越大, 表示光圈越小, 进光量越少

标准的光圈级数为:$f/1,f/1.4,f/2,f/2.8,f/4,f/5.6,f/8,f/11,f/16,f/22,f/32$. 这些数值是相邻级数的二倍关系

Rayleigh判据

望远镜的像分辨能力

当一个圆斑像的中心刚好落在另一圆斑像的边缘（第一暗纹）上时, 被认为刚刚能被分辨. 由此定义的最小分辨角为:

$$\delta {\theta }_m=1.22\frac{\lambda }{D}$$

由此可知, 如果要提高望远镜的分辨本领, 光提升它的放大率是无效的, 因为它在放大像的同时把衍射光斑也一起放大了. 所以要提升望远镜的分辨率, 最有效的方法是增大它物镜的口径

另一方面, 望远镜的放大率太小显然也是不行的, 因为这将无法最大地利用它的分辨本领. 因此, 我们在选择目镜时, 需要能使总放大率能将仪器的最小分辨角放大到人眼所能分辨的最小角度$1^{\prime }\approx 2.9\times 10^{-4}\mathrm{rad}$, 由此我们可以定义望远镜的有效视角放大率

$$M_m=\frac{\delta {\theta }_e}{\delta {\theta }_m}$$

回忆

望远镜的放大率公式为

$$M=\frac{f_O}{f_E}$$

显微镜的像分辨能力

显微镜的最小分辨距离为

$$\delta y_m=\frac{0.61\lambda }{n\sin u}=0.61\frac{\lambda }{N.A.}$$

其中$N.A.=n\sin u$称为显微镜的数值孔径, 这里不取$1.22$而取$0.61$是因为$y$表示某处像点和中心点的距离, 对应于Airy斑的半径. 由此我们可以给出提升显微镜分辨本领的方法

• 可以通过油浸增大显微镜的数值孔径, 从而提升它的分辨能力
• 也可以通过使用短波长的光来提升分辨能力

由于人眼可以分辨的最小距离

$$\delta y_e=s_0\delta {\theta }_e=25\mathrm{cm}\times \left(2.9\times 10^{-4}\mathrm{rad}\right)=72.5\mu \mathrm{m}$$

故我们也可以定义显微镜的有效放大率

$$M=\frac{\delta y_e}{\delta y_m}$$

回忆

显微镜的放大率公式为

$$M=V_O{M}_E=-\frac{\Delta }{f_O}\frac{s_0}{f_E}$$

多缝衍射

定义$d$为缝和缝之间的距离（即缝的空间周期）, 每个缝的宽度为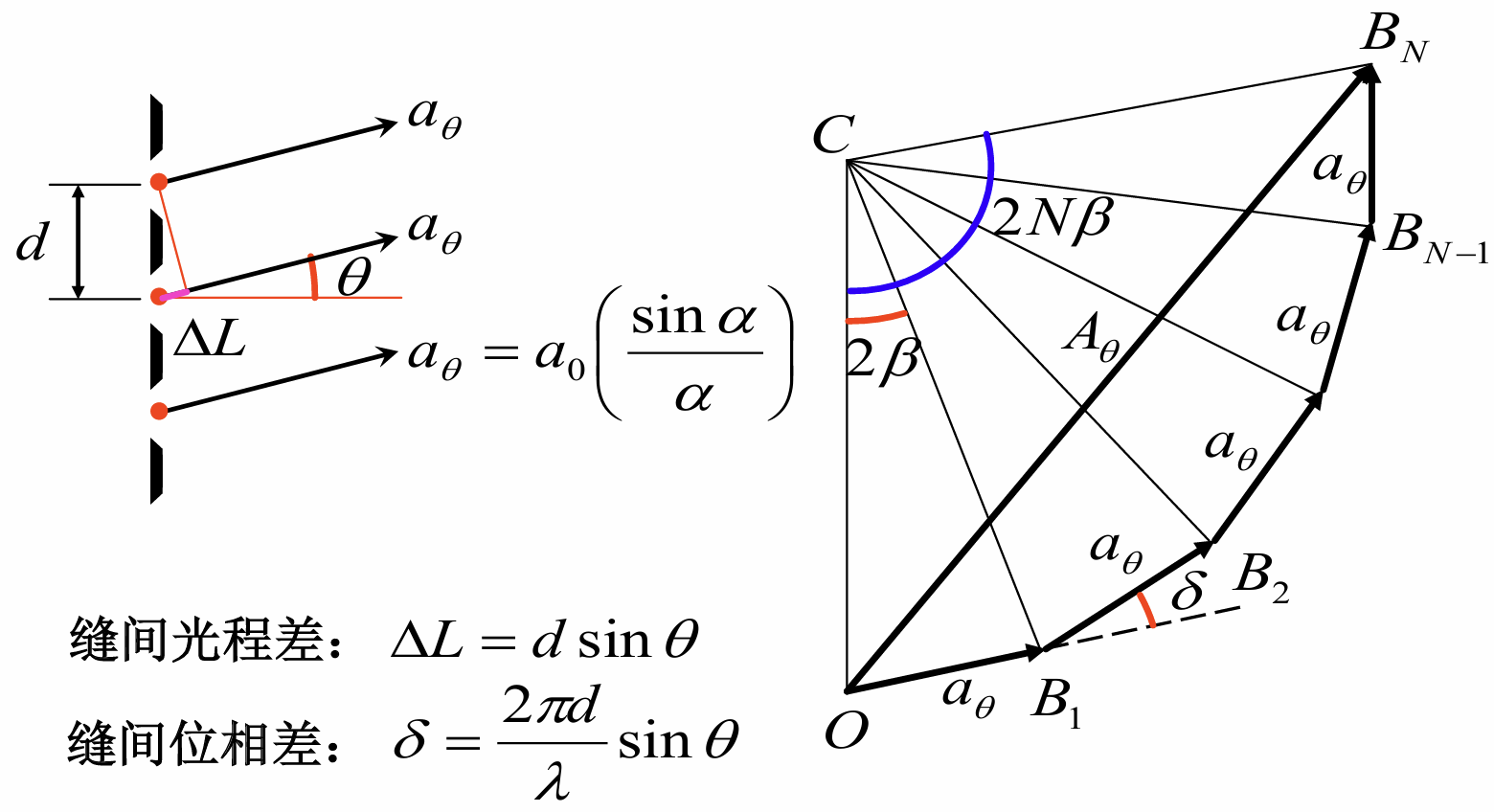$a$, 考虑$\theta$处的衍射 设$\alpha =\frac{\pi a}{\lambda }\sin \theta$, 则每一个缝贡献的振幅为$a_{\theta }=a_0\left(\frac{\sin \alpha }{\alpha }\right)$, 而每相邻两个缝之间的的光程差为$\Delta L=d\sin \theta$, 对应的相位差就是$\delta =\frac{2\pi d}{\lambda }\sin \theta$, 再设$\beta =\frac{\delta }{2}=\frac{\pi d}{\lambda }\sin \theta$, 则我们可以作出上面的振幅矢量合成图（假设一共有$N$个缝）

设半径$R=\overline{CO}=\overline{C{B}_N}$, 则有

$$a_{\theta }=2R\sin \beta ,A_{\theta }=2R\sin N\beta ⟹A_{\theta }=a_{\theta }\frac{\sin N\beta }{\sin \beta }$$

得到光强公式

$$I_{\theta }=A_{\theta }^2=a_0^2{\left(\frac{\sin \alpha }{\alpha }\right)}^2{\left(\frac{\sin N\beta }{\beta }\right)}^2$$

其中$\left(\frac{\sin \alpha }{\alpha }\right)$为单缝衍射因子, $\left(\frac{\sin N\beta }{\sin \beta }\right)$为缝间干涉因子, 它们的图像分别如下面的(a),(b)所示, (c)是它们合成后的图像 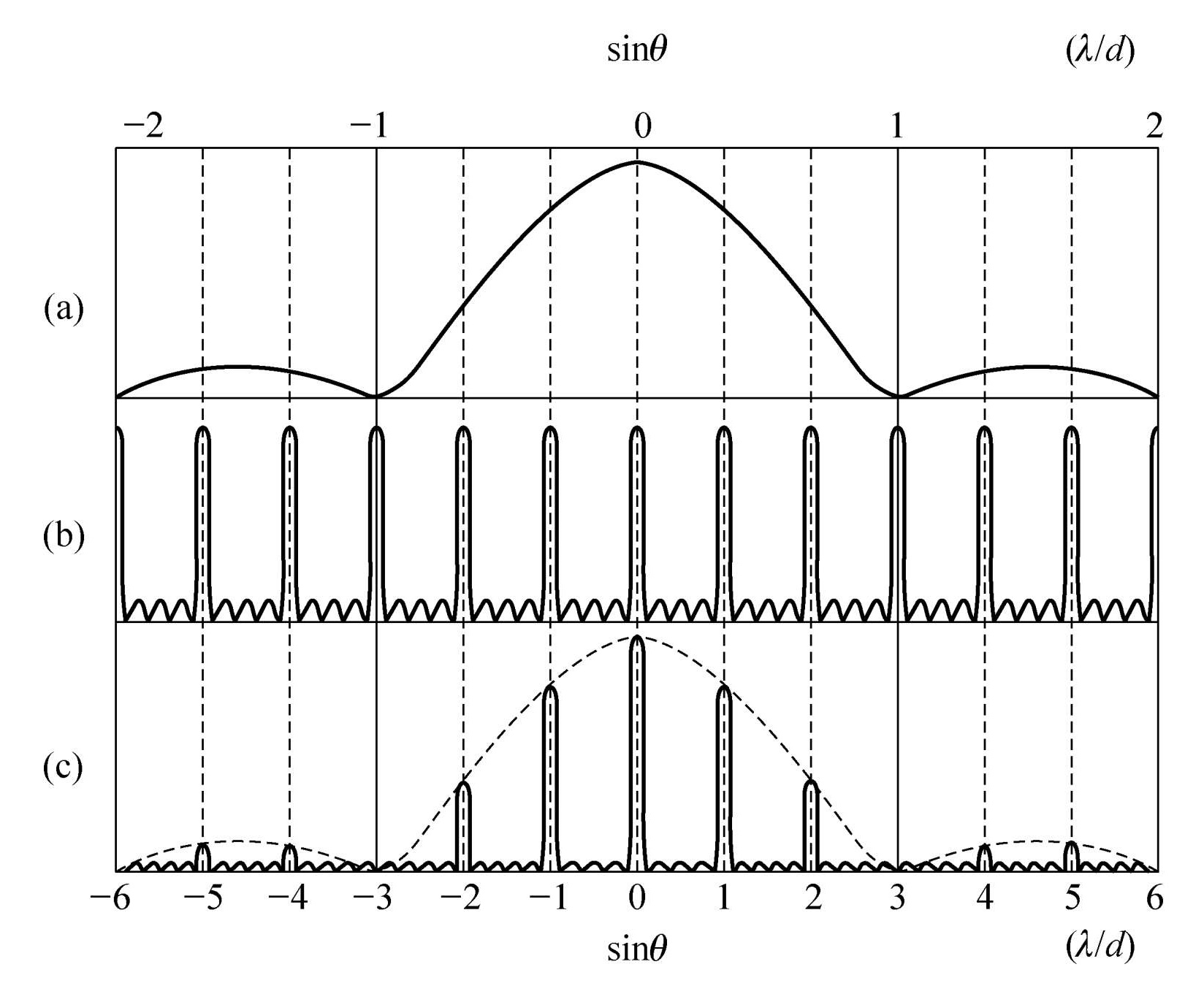一个对(c)图像的描述是

• 微观决定宏观 - 缝的大小决定图样的宏观结构（外包络）
• 宏观决定微观 - 缝和缝的间距决定图样的微观结构（每一个次极大）

类似于多缝干涉, 多缝衍射的图样存在主极大（所以$\Delta L=k\lambda$的时候对应得是干涉的极大, 而不是衍射的极小）

$$d\sin \theta =k\lambda ⟹\sin \theta =k\frac{\lambda }{d},k=0,\pm 1,\pm 2,\dots$$

考虑图样的暗点, 也就是缝间衍射因子的零点, 我们可以解得

$$\frac{\sin N\beta }{\sin \beta }=0⟹N\beta =m\pi ,\beta \ne n\pi$$

又因为$\beta =\frac{\pi d}{\lambda }\sin \theta$, 所以我们得到零点的位置

$$\sin \theta =\left(k+\frac{m}{N}\right)\frac{\lambda }{d},k=0,\pm 1,\pm 2,\dots ;m=1,2,\dots ,N-1$$

其中$m=N$的情况恰好对应于主极大, 每两个主极大之间有$N-1$个暗点, 而每两个相邻的暗线之间都有一个次极大, 也就是说每两个主极大之间都有$N-2$个次极大

因为每一个主极大不是两两紧挨的, 所以我们不能采用单缝衍射中的方法来计算主极大的半角宽, 而需要通过

$$\sin {\theta }_k=k\frac{\lambda }{d},\sin ({\theta }_k+\Delta {\theta }_k)=\left(k+\frac{1}{N}\right)\frac{\lambda }{d}$$

来给出

$$\Delta {\theta }_k\cos {\theta }_k=\sin ({\theta }_k+\Delta {\theta }_k)-\sin {\theta }_k=\frac{\lambda }{Nd}⟹\Delta {\theta }_k=\frac{\lambda }{Nd\cos {\theta }_k}$$

当某一个主极大恰好被单缝衍射因子调制为$0$的时候, 我们称这种情况为缺级, 它满足

$$\sin \theta =k\frac{\lambda }{a}=k^{\prime }\frac{\lambda }{d}$$