Phase Transition

物态和相

物态

大量的微观粒子在一定的热力学状态(温度和压强)下相互聚集为一种稳定的结构状态, 这种状态就是“物质的一种状态”, 简称物态

相

热力学平衡态下, 物理、化学性质完全相同的均匀物质的聚集态称为物质的一个相, 即系统中物理、化学性质均匀的部分, 它和其它部分之间有一定的分界面隔离开来

几点说明:

• 物态是物质(系统)的一个平衡态, 但不一定是均匀的
• 一个物态中可能存在多个相, 即多相共存；
• 一个相是均匀的, 但不一定是一种化学成分
• 相与相之间有分界面, 可以通过物理或机械的办法分开

也就是说

$$\mathrm{单元均匀系}\subset \mathrm{相}(\mathrm{多元同相})\subset \mathrm{物态}$$

举例

• 冰水混合物为系统的一个物态, 其中冰和水是两个不同的相, 故系统是一个单元复相系；
• 酒精溶于水, 酒精和水的混合物为一相, 故系统是一个多元单相系；
• 气体或气体混合物一般只有一个相, 即气相；
• 对于固体, 不同点阵结构的物理性质不同, 分属不同的相.

凝聚态

凝聚态物质指的是原子或分子间具有较强相互作用力, 使得物质呈现出较为固定的结构和形态. 主要包括固态、液态、玻璃态、超流态等等

非凝聚态

非凝聚态物质的原子或分子间相互作用力较弱, 物质的结构较为松散, 主要有气态和等离子态等

相变

相变: 在一定条件下物质从一种相转变为另一种相的变化过程, 即系统的物质结构发生变化的过程称为相变, 相变可以分为两类

• 狭义相变: 过程前后系统的化学组成不变, 即不发生化学反应；
• 广义相变: 包括过程前后化学组成的变化；

当压强确定时, 相变是在一个确定的温度下发生的；当温度确定时, 相变是在一个确定的压强下发生的；在相变点(确定温度和压强)处系统可多相共存, 为复相系.

相变是大量粒子相互作用的结果, 是宏观集体现象；在相变的过程中, 系统的物理特征参量发生不连续变化, 即突变（但是参量的导数可以不连续）

相变的本质是有序和无序两种倾向的竞争: 相变是由构成系统的微观粒子之间的相互作用（倾向于使系统有序）与微观粒子本身的热运动（使系统无序）相互竞争的结果

单元系的复相平衡

开放系统的化学势和热力学方程

开放系统即可以与环境交换物质和能量的系统

开放系统与环境仍然可以达到平衡态. 因为系统的物质的量不确定, 对该平衡态的描述需要引入一个新的热力学参量, 即化学势.

化学势$\mu$与物质的量（摩尔数$\nu$）构成共轭的热力学参量

开放系统的热力学微分方程: 对于一个开放系统, 除传热和做功可引起系统内能改变外, 物质的量的变化也将导致内能的改变

$$\begin{array}{rl}& \mathrm{d}U=T\mathrm{d}S-p\mathrm{d}V+\mu \mathrm{d}\nu \\ & \mathrm{d}H=T\mathrm{d}S+V\mathrm{d}p+\mu \mathrm{d}\nu \\ & \mathrm{d}F=-S\mathrm{d}T-p\mathrm{d}V+\mu \mathrm{d}\nu \\ & \mathrm{d}G=-S\mathrm{d}T+V\mathrm{d}p+\mu \mathrm{d}\nu \end{array}⟹\mu =\{\begin{array}{l}{\left(\partial U/\partial \nu \right)}_{S,V}\\ {\left(\partial H/\partial \nu \right)}_{S,p}\\ {\left(\partial F/\partial \nu \right)}_{T,V}\\ {\left(\partial G/\partial \nu \right)}_{T,p}\end{array}$$

化学势

考虑一等温等压的物质增加过程, 可知

$$\mu =\frac{G\left(T,p,\nu \right)}{\nu }=G_m\left(T,p\right)=U_m+p{V}_m-T{S}_m$$

即化学势是等温等压条件下 1 mol 物质的自由焓 同理

• 化学势是等温等体条件下 1 mol 物质的自由能；
• 化学势是等熵等压条件下 1 mol 物质的焓；
• 化学势是等熵等体条件下 1 mol 物质的内能

$$\mathrm{d}\mu =\mathrm{d}{G}_m(T,p)=-S_m\mathrm{d}T+V_m\mathrm{d}p$$

相平衡条件

设$1$和$2$是一个单元系的已经达到平衡的任意两个相, 且这两个相构成一个孤立系统, 则系统的总内能$U_1+U_2$、总体积$V_1+V_2$和物质的量 ${\nu }_1+{\nu }_2$ 都守恒.

设想“$1$”相和“$2$”相发生了一个无穷小的变动, 由孤立系统的条件有

$$\mathrm{d}{U}_1+\mathrm{d}{U}_2=\mathrm{d}{V}_1+\mathrm{d}{V}_2=\mathrm{d}{\nu }_1+\mathrm{d}{\nu }_2=0$$

该变化过程中, “$1$”相和“$2$”相单独形成一个开放系统, 由其热力学微分方程可得

$$\begin{array}{r}\mathrm{d}{S}_1=\frac{1}{T_1}\left(\mathrm{d}{U}_1+p_1\mathrm{d}{V}_1-{\mu }_1\mathrm{d}{\nu }_1\right)\\ \mathrm{d}{S}_2=\frac{1}{T_2}\left(\mathrm{d}{U}_2+p_2\mathrm{d}{V}_2-{\mu }_2\mathrm{d}{\nu }_2\right)\end{array}$$

系统的总熵变

由孤立系统热平衡条件可知, 当“1”相和“2”相间达到平衡时, 系统总的熵有极大值, 即

$$\mathrm{d}S=\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\mathrm{d}{U}_1+\left(\frac{p_1}{T_1}-\frac{p_2}{T_2}\right)\mathrm{d}{V}_1-\left(\frac{{\mu }_1}{T_1}-\frac{{\mu }_2}{T_2}\right)\mathrm{d}{\nu }_1=0$$

由于$\mathrm{d}U,\mathrm{d}V,\mathrm{d}\nu$独立改变, 所以两相平衡的条件为

1. 热学平衡$T_1=T_2$
2. 力学平衡$p_1=p_2$
3. 化学平衡${\mu }_1={\mu }_2$

相平衡条件不满足时, 系统中过程进行的方向

• 热学平衡不满足时, 热量从高温相传递到低温相
• 力学平衡不满足时, 则压强大的相膨胀, 而压强小的相将收缩；
• 化学平衡不满足时, 物质从化学势高的相向化学势低的相转移.

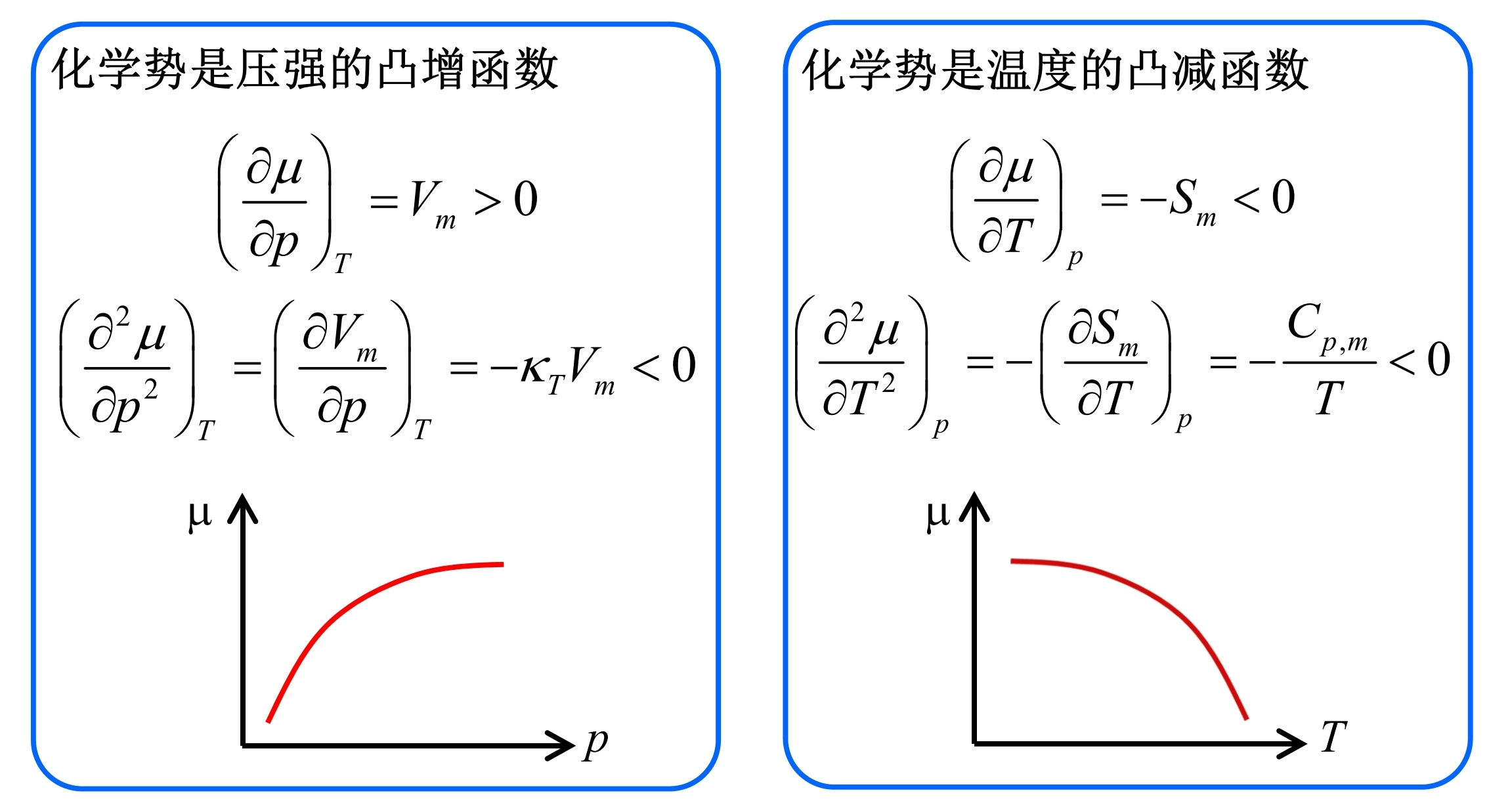
相变和相图

• $T=T_c$时相平衡, 两相共存
• $T>T_c$时$2$相更加稳定, 所有物质转移到$2$相
• $T<T_c$时$1$相更加稳定, 所有物质转移到$1$相

相变分类

根据化学势导数的连续性可对相变的类型分类

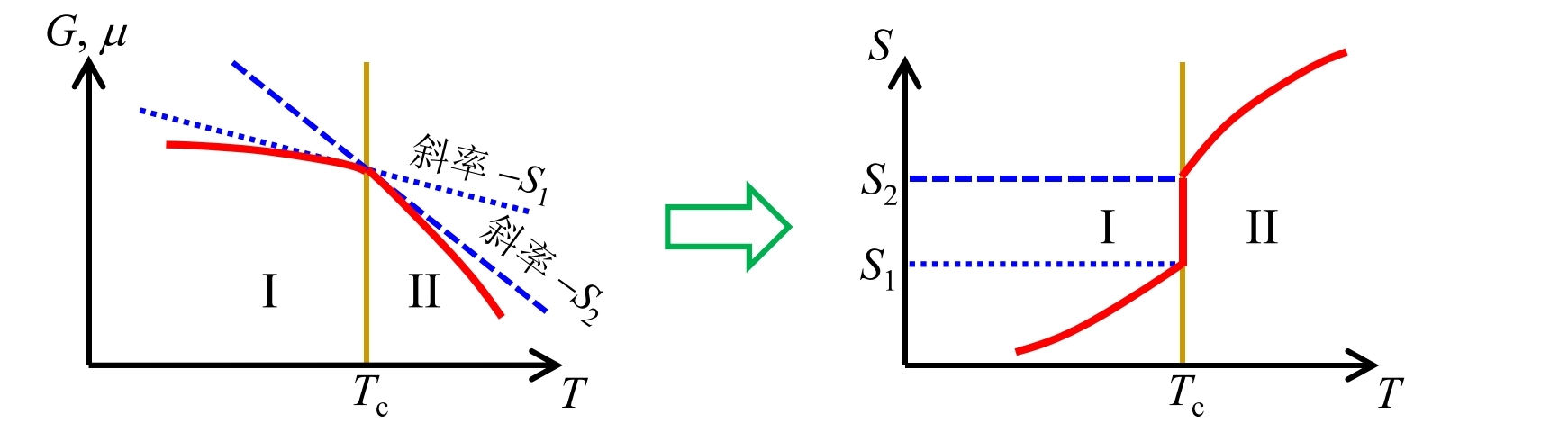
• 一级相变: 相变处两相的化学势相等, 但它们的一阶导数不相等；即在相变处, 系统的化学势连续, 但其一阶导数不连续；
• 二级相变: 相变处系统的化学势及其一阶导数连续, 但其二阶导数不连续
• $K(K>2)$ 级相变: 相变处, 系统的化学势及其 $k(k=1,2,\dots ,K-1)$ 阶导数连续

通常把二级及二级以上的相变统称为连续相变

另一种相演化: 热力学函数及其任意阶偏导数都连续的相演化过程(非相变) 称为连续过渡 (Crossover)

相和相变的另一种理解

• 相: 系统化学势在热力学状态空间中为解析函数 (任意阶导数都连续, 没有突变) 的物理状态；
• 相变: 系统化学势出现非解析的点, 即其导数出现不连续或发散.

相变举例

• 一级相变: 固液、固气及液气相变, 固-固相变.
• 二级相变: 铁磁-顺磁相变, 液氦的正常液相到超流相的相变, 超导体的正常态到超导态
• 连续过渡: BCS-BEC crossover: 微观原子核的不定轴转动到定轴转动之间的演化, 系统的宏观性质没有突变, 仅转动轴的取向发生了变化.

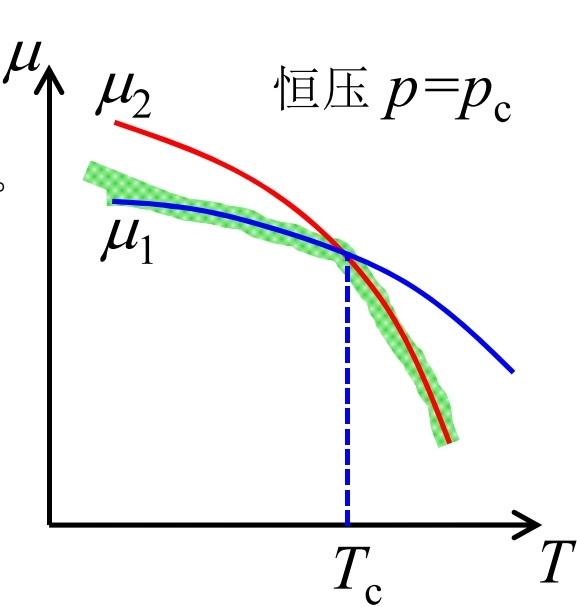
相图

• 蓝线: 汽化曲线, 液、汽相平衡线；
• 绿线: 熔解曲线, 固、液相平衡线；
• 红线: 升华曲线, 固、汽相平衡线. 三相点（triple point）: 气、液、固三相共存状态

$${\mu }_{\text{gas}}(T_{\text{tp}},p_{\text{tp}})={\mu }_{\text{liquid}}(T_{\text{tp}},p_{\text{tp}})={\mu }_{\text{solid}}(T_{\text{tp}},p_{\text{tp}})$$

临界点（critical point）: 在此温度、压强之上, 气体和液体无法区分, 成为同一个相； 液气之间的变化为连续过渡.

熔解曲线（绿线）没有终点: 固体的晶体结构具有一定的对称性, 对称性只能是“有”或“无”, 而不能兼而有之

一级相变

考虑等温等压条件, 相变处的化学势（或者自由焓）连续, 但是其一阶导数不连续

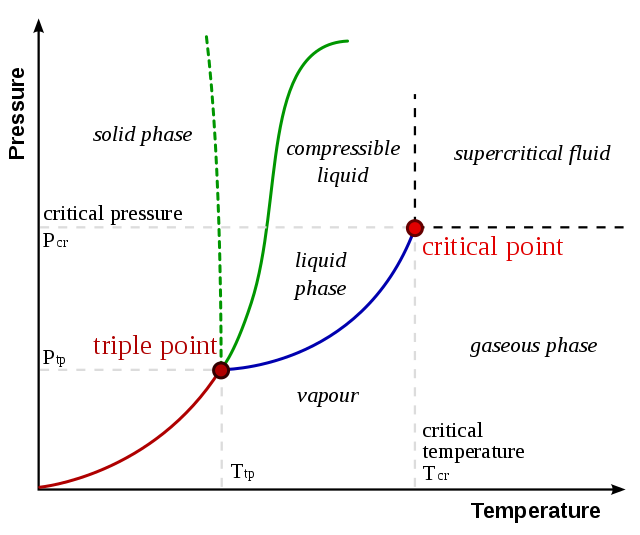
基本特征

体积跃变和相变功

由化学势的定义

$${\left(\frac{\partial {\mu }_1}{\partial p}\right)}_T\ne {\left(\frac{\partial {\mu }_2}{\partial p}\right)}_T⟹V_{m1}\ne V_{m2}$$

所以一级相变过程中, 存在相变功$W=p(V_2-V_1)\ne 0$

相变潜热

$${\left(\frac{\partial {\mu }_1}{\partial T}\right)}_T\ne {\left(\frac{\partial {\mu }_2}{\partial T}\right)}_T⟹S_{m1}\ne S_{m2}$$

定义相变潜热

1 atm下, 1 kg 0${}^{\circ }\mathrm{C}$ 的冰要吸收 79.6 kcal 的热量才能转变为同温度的水, 1 kg 100${}^{\circ }\mathrm{C}$ 的水要吸收539 kcal的热量才能转变成同温度的水蒸气, 它们分别对应固液相变和液气相变的相变潜热

Clapeyron方程

由单元系的复相平衡条件得到的一级相变相平衡曲线的斜率与相变温度、潜热和两相摩尔体积差之间的关系称为Clapeyron方程

沿一相平衡曲线把系统的温度和压强从$T,p\to T+\mathrm{d}T,p+\mathrm{d}p$

$$\begin{array}{rl}{\mu }_1(T,p)& ={\mu }_2(T,p)\\ {\mu }_1(T+\mathrm{d}T,p+\mathrm{d}p)& ={\mu }_2(T+\mathrm{d}T,p+\mathrm{d}p)\\ ⟹\mathrm{d}{\mu }_1(T,p)& =\mathrm{d}{\mu }_2(T,p)\end{array}$$

利用$\mathrm{d}\mu =-S_m\mathrm{d}T+V_m\mathrm{d}p$, 可得

$$\frac{\mathrm{d}p}{\mathrm{d}T}=\frac{S_{m2}-S_{m1}}{V_{m2}-V_{m1}}=\frac{L_m}{T(V_{m2}-V_{m1})}$$

其中$L_m=T(S_{m2}-S_{m1})$为平衡相变中的摩尔潜热

注意

Clapeyron方程描述的是相平衡曲线的性质, 它描述的是一种平衡状态, 而不是相变过程

单元系气、液、固相变的性质

液气相变

• 液体汽化时吸热, 且体积膨胀, 所以液气相变是一级相变；
• 相平衡曲线 (汽化曲线) 的斜率为正；
• 液体的沸点随压强的增强而升高.

固气相变

• 固体升华时吸热, 且体积膨胀, 所以固气相变是一级相变；
• 相平衡曲线 (升华曲线) 的斜率为正；
• 固体的升华点随压强的增强而升高.

固液相变

• 固体熔解时吸热, 且体积有跃变, 所以固液相变是一级相变；
• 取决于熔解时体积是膨胀还是收缩, 相平衡曲线 (熔解曲线) 的斜率可正可负；
  • $\mathrm{C}{\mathrm{O}}_2$: 体积膨胀, 斜率为正；
  • ${\mathrm{H}}_2\mathrm{O}$: 体积收缩, 斜率为负.
• 随着压强的增强, 固体的熔点可能升高 ($\mathrm{C}{\mathrm{O}}_2$), 也可能减低 (${\mathrm{H}}_2\mathrm{O}$).

气液相变的讨论

液体转变成气体的汽化过程是液体的一些组分粒子克服其它组分粒子的吸引作用而逸出液体的过程, 有两种形式:

• 蒸发 (evaporation): 在任何温度下, 液体表面发生的汽化现象；
• 沸腾 (boiling): 在沸点温度下, 液体内部进行的汽化现象；

当物质的温度达到沸点时, 其汽化方式主要是沸腾；而当温度低于沸点时, 其汽化方式只有蒸发；

从相变机制上看, 蒸发和沸腾并无本质区别. 沸腾时相变仍是在气液分界面上以蒸发的方式进行, 只是液体内部涌现大量气泡, 从而大大增加了气液之间的分界面.

蒸发与凝结 饱和蒸汽压

蒸发的微观机制

蒸发是液体分子从液面跑出来的过程. 分子从液面跑出来时, 需在表面层中克服液体分子间的引力做功, 所以跑出来的分子是热运动动能较大的分子；

若不从外界补充能量, 蒸发导致液体变冷；(保持温度, 汽化潜热), 另一方面, 蒸气分子也会不断地返回液体中去, 凝结成液体；

因此, 液体蒸发的数量, 是上述两种相反过程相抵消后的剩余部分, 即液体分子跑出来的数目减去蒸气分子返回液体的数目.

影响蒸发的因素

• 表面积: 表面积越大, 蒸发越快；
• 温度: 温度越高, 蒸发越快；
• 通风: 通风情况越好, 蒸发越快.

饱和蒸汽压

在密闭容器里, 随着蒸发的进行, 单位时间内跑出液体的分子数和返回液体的分子数趋于相等, 宏观上蒸发现象停止. 这种与液体保持动态平衡的蒸气称为饱和蒸气, 其压强称为饱和蒸气压.

容易蒸发的液体饱和蒸气压大, 不易蒸发的液体饱和蒸气压小, 如在 20${}^{\circ }\mathrm{C}$时, 乙醚 ($5.82\times 10^4$ Pa), 酒精 ($5.93\times 10^3$ Pa), 水 ($2.33\times 10^3$ Pa) ；

影响饱和蒸汽压的因素

• 饱和蒸气压随温度的升高而增大；
• 饱和蒸气压与蒸气所占体积无关, 与该体积中有无其它气体无关 (即饱和蒸汽压表示的是该蒸气的分压强)；
• 饱和蒸气压与液面形状有关.

Tip

饱和蒸汽压也可以推广到固气相变中, 比如说冰的饱和蒸汽压表示冰-水蒸气系统保持动态平衡时水蒸气的压强

汽化曲线

即气液两相平衡曲线

• 对应的压强为饱和蒸气压, 温度为沸点；
• 汽化曲线有终点, 临界温度$T_c$；
• 汽化吸热且膨胀, 故汽化曲线斜率为正.

汽化潜热

即液体在等压的条件下通过蒸发全部转变成等温蒸气的过程所需的热量, 包括两部分:

• 克服液体内其它液体分子对它的吸引力, 对平面液面, 该部分所需的功等于气态分子和液态分子的内能差 (内潜热)；
• 对抗液面上已经形成的蒸气压, 等于 $p\Delta V$, 其中$\Delta V$是气态分子与液态分子平均占据的体积差 (外潜热)；

$$L=(U_2-U_1)+p(V_2-V_1)=(\Delta H{)}_{T,p}$$

当温度达到临界温度$T_c$ 时, 气液两相的差别消失, 汽化潜热应为$0$；故可预期汽化潜热随温度的上升而下降

曲面液体的饱和蒸气压

蒸发是液体表面上发生的汽化行为, 因此液体表面的性质, 如表面张力、密度、曲率等性质都会改变液体和蒸汽之间的平衡条件, 从而对饱和蒸气压产生影响

液体表面的性质决定汽化潜热, 从而影响饱和蒸汽压.

事实上有

$$p_0\propto \exp \left(-\frac{L_m}{RT}\right)$$

凸曲面液体上的饱和蒸气压大于平面液体上的饱和蒸汽压 液体分子从凸液面跃出时所需消耗的能量比从平面液面跃出的小, 即凸面液体分子的汽化潜热小于平面液体分子的汽化潜热.

凹曲面液体上的饱和蒸气压小于平面液体上的饱和蒸汽压 液体分子从凹液面跃出时所需消耗的能量比从 平面液面跃出的大, 即凹面液体分子的汽化潜 热大于平面液体分子的汽化潜热.

过饱和蒸气

在蒸气凝结的初阶段, 形成的液滴很小, 相应的饱和蒸气压就很大；因此, 有时蒸气压超过平面上饱和蒸气压, 但液滴仍不能形成并长大的现象, 这种现象称为过饱和现象；对应的蒸气称为过饱和蒸气或过冷蒸气.

凝结核、云及人工降雨

• 凝结核: 尘埃和杂质等小微粒、带电粒子和离子；
• 暖云: 大小雨滴$\to$小雨滴蒸发, 大雨滴长大$\to$雨；
• 冷云由冰晶组成, 混合云由冰晶和水滴组成；
• 人工降雨: 干冰降温, 碘化银做凝结核.

云室

利用过饱和蒸气显示高能带电粒子运动轨迹的仪器. 由英国物理学家 C.T.R. Wilson 发现, 1927年诺贝尔物理奖； 英国物理学家 P.S. Blackett 改进了云室法, 并以此在核物理学宇宙射线领域取得重大成果并获得1948年诺贝尔物理奖.

沸腾

在一定压强下, 加热液体达到某一温度时, 液体内部和器壁上涌现出大量的气泡, 整个液体上下翻滚剧烈汽化, 这种现象称为沸腾, 相应的温度称为沸点.

液体内气泡的平衡条件

设$p$是外界气压, $p_0$是气泡内蒸汽的饱和蒸汽压, 而$\frac{\nu RT}{V}$是气泡内其他气体的压强, 则有

$$p_0(T)+\frac{\nu RT}{V}=p+\Delta p,\Delta p=\frac{2\gamma {\left(\frac{4\pi }{3}\right)}^{1/3}}{V^{1/3}}$$

• 当温度不高时 $(p_0<p)$, 升高一点温度, 气泡可增大体积并维持平衡；
• 当温度达到某一温度时, $p_0=p$ , 气泡的平衡无法再维持；此时气泡剧然胀大, 并在浮力下迅速上升, 到液面时破裂开来, 放出里面的蒸气.

**沸腾现象的条件是液体的饱和蒸气压（即液泡内气体的压强）等于或大于外界压强. 密闭容器中的液体不能沸腾. **

沸点

• 饱和蒸气压等于外界压强时的温度称为沸点；
• 沸腾过程中, 系统吸热但温度不变$\to$汽化潜热；
• 沸点温度随压强的增大而升高.

过热液体、暴沸

液体内部和器壁上的小气泡起着汽化核的作用；当液体缺少汽化核时, 可以加热到沸点以上还不沸腾, 这种液体称为过热液体；过热液体中的密度涨落可能导致暴沸.

气泡室

是利用过热液体显示高能带电粒子运动轨迹的仪器. 美国科学家 D.A. Glaser 发现, 获1960年诺贝尔物理奖；美国科学家 L.W. Alvarez发展了气泡室和数据分析技术, 从而发现了大量共振态而获得1968年诺贝尔物理奖.

气液等温相变

将$1\mathrm{mol}$某种实际气体装入一封闭气缸, 把气缸置于温度为$T$的恒温热源中, 对他进行等温压缩 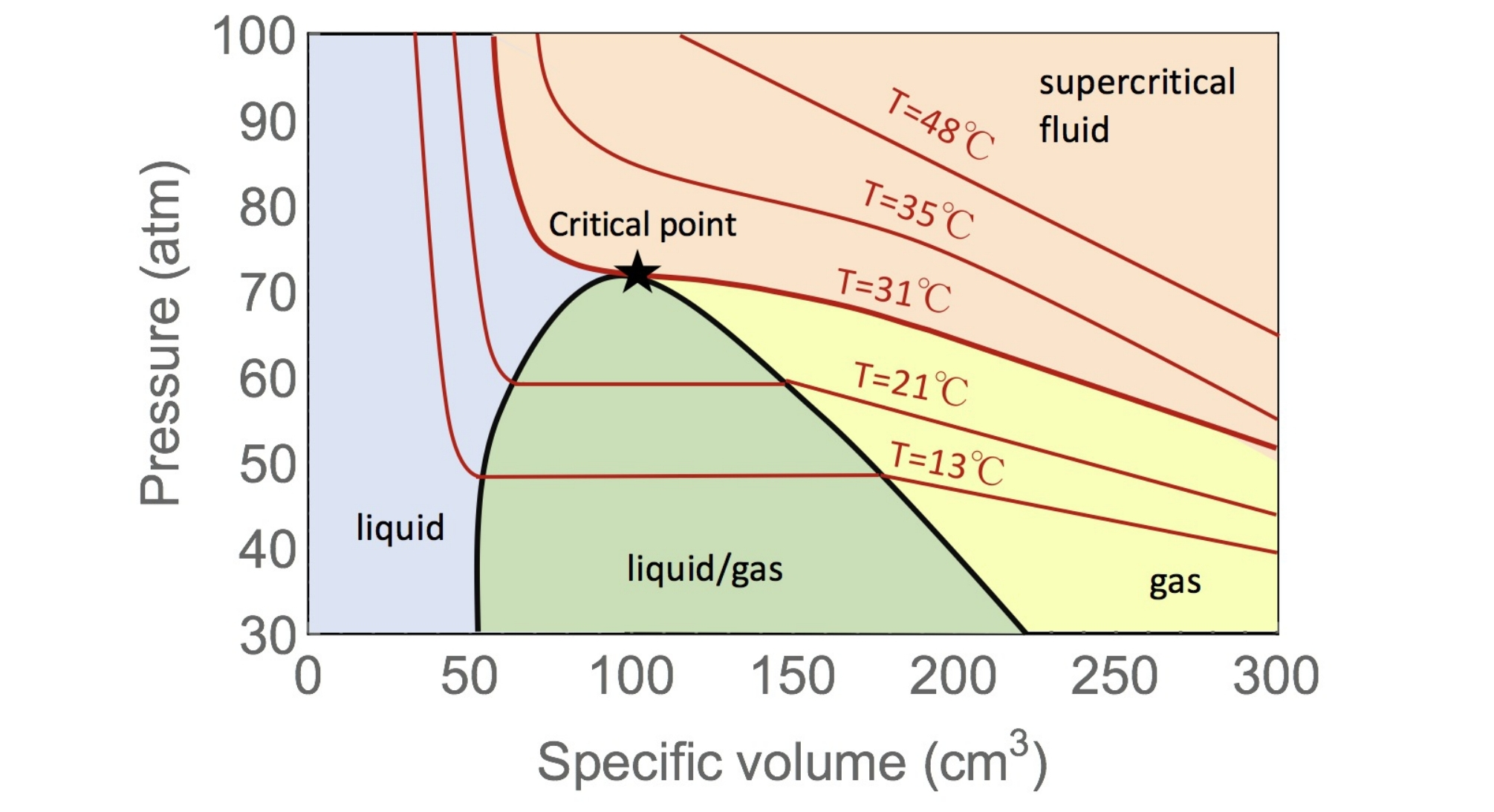上图是$\mathrm{C}{\mathrm{O}}_2$的等温相变图, 可以看出在温度较低（$T=13^{\circ }\mathrm{C}$）时, 过程可以分为三个阶段

1. 气态, 压强随着体积减小而增大
2. 气液共存区, 对系统的压缩不会导致升压, 压强为饱和蒸气压；在此过程中, 饱和蒸汽逐渐被压缩成同温同压的液体
3. 液态, 由于液体的等温压缩系数小曲线更为陡峭

而当温度大于临界温度（$T_c$）时, 就不存在相变和两相共存现象, 此时气体无法液化. 临界现象的表现是: 气液不分, 液面消失

临界乳光现象: 在临界状态下, 液相和气相之间频繁交换分子, 使得光在其上的散射增强, 原来透明的气体或液体变得浑浊起来, 呈现一片乳白色的现象, 是临界现象的典型特征

Van der Waals等温线

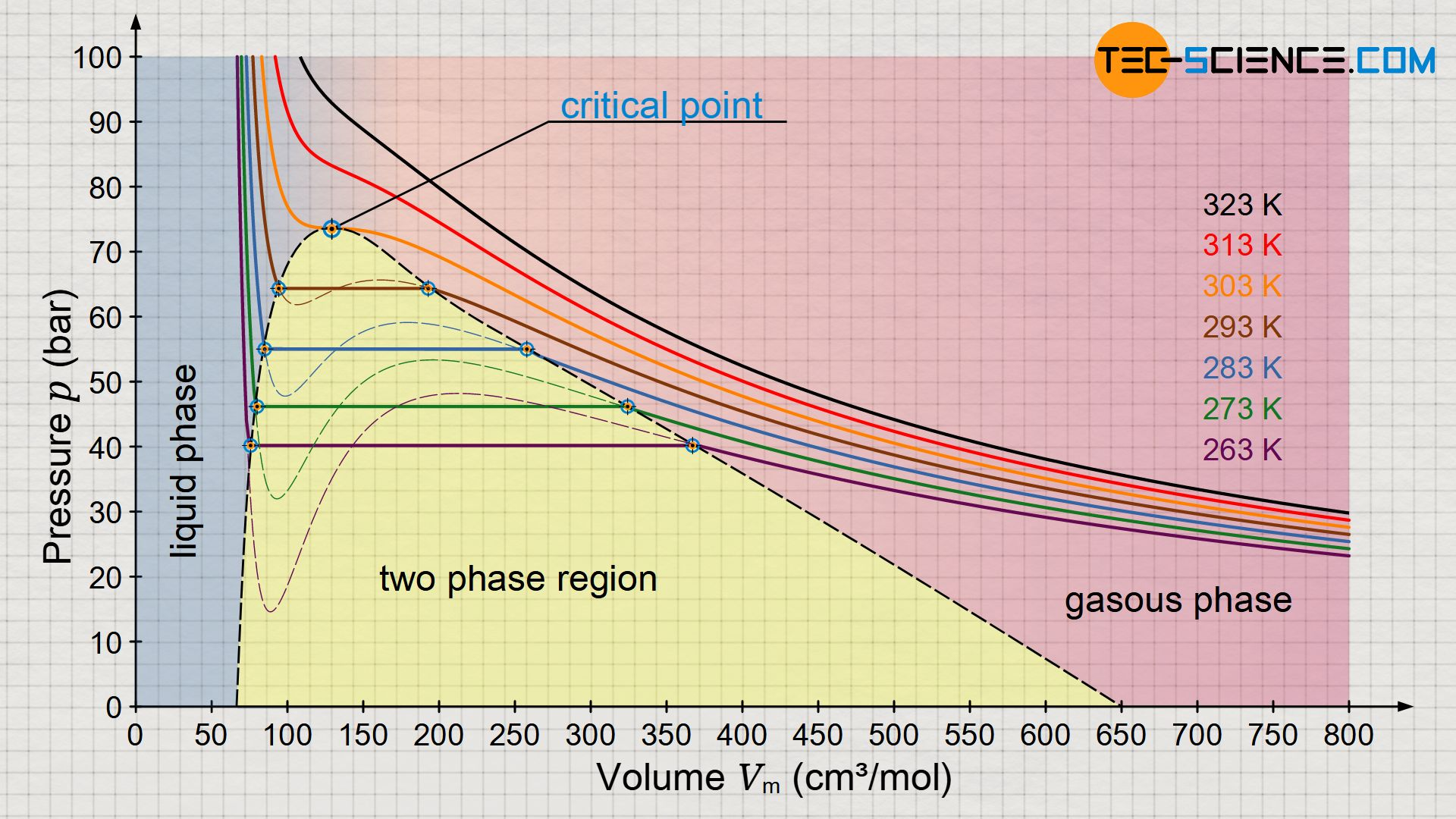即曲线

$$(p+\frac{a}{V_m^2})(V_m-b)=RT$$

可以观察到

• 温度越高, Van der Waals等温线越接近理想气体等温线
• 温度在临界温度之上时, 压强是体积的单调递减函数；在临界温度之下时, 压强不再是体积的单调递减函数

极值轨道

等温线上压强取极值的点$\left(\frac{\partial p}{\partial V_m}=0\right)$连成的线称为极值轨道, 可计算其方程为

$$\left(\frac{\partial p}{\partial V_m}\right){|}_{\text{extreme}}=0⟹p_{\text{extreme}}{V}_{m,\text{extreme}}=a(V_{m,\text{extreme}}-2b)$$

简记下标$\text{extreme}$为$\text{e}$, 则有

$$\frac{{\partial }^{2}p}{\partial V_m^2}{|}_e=\frac{RT}{V_{m,e}}\frac{(3b-V_{m,e})}{(V_{m,e}-b{)}^3}$$

极值轨道上的拐点, 即极小和极大值的交接点, 就是临界点, 令上面算出的一阶和二阶导数均为$0$, 则可得

$$V_{m,c}=3b,p_c=\frac{a}{27b^2},T_c=\frac{8a}{27Rb}$$

Van der Waals方程的不足

• 在低温区会导致负压, 在$T=0$时达到最低值$p_{\text{min}}=-\frac{a}{b^2}$
• 无法描述气液共存时压强不变的情况
• 等温曲线存在斜率为正的线段, 这表明压缩系数${\kappa }_T=-\frac{1}{V}{\left(\frac{\partial V}{\partial p}\right)}_T<0$, 即系统是不稳定的

正压区的方程

为了更好地描述气液共存的状态, 我们可以对Van der Waals等温线作出修正, 使得在气液共存时用一条等压线代替本来的等温曲线

此时有Maxwell等面积法则: 我们需要画的那一条等压线需要满足其和上方曲线围成的面积与其和下方曲线围成的面积相等

气液共存时两相的物质的量之间的关系

记系统总的物质的量为$\nu$, 两相平衡时系统的摩尔体积为$V_m$, 定义两相的摩尔密度

$$x_{\text{liq}}=\frac{{\nu }_{\text{liq}}}{\nu },x_{\text{gas}}=\frac{{\nu }_{\text{gas}}}{\nu }$$

于是有

$$\{\begin{array}{l}{x}_{\text{liq}}+x_{\text{gas}}=1\\ x_{\text{liq}}{V}_{m,\text{liq}}+x_{\text{gas}}{V}_{m,\text{gas}}=V_m\end{array}$$

可以解得

$$x_{\text{liq}}=\frac{V_{m,\text{gas}}-V_m}{V_{m,\text{gas}}-V_{m,\text{liq}}},x_{\text{liq}}=\frac{V_m-V_{m,\text{liq}}}{V_{m,\text{gas}}-V_{m,\text{liq}}}$$

由此得到系统的总自由能为

$$F=x_{\text{gas}}{F}_{\text{gas}}+x_{\text{liq}}{F}_{\text{liq}}$$

过冷蒸汽和过热液体

在上图的Van der Waals等温线中, BCD段上任意点的等温压缩系数为负数, 是热力学系统的不稳定状态, 在实验中不可能观测到

我们设通过Maxwell等面积法则确定的直线和Van der Waals等温线的交点分别为A和E, 我们发现AB和DE段上的任意点的压缩系数为正, 是热力学系统可能存在的态. 实际上, 这两段对应的物态是亚稳态, 它们比相应的AB'线段和D'E线段上相应的态的自由能要更高

由定义, 在等温状态下

$$F_{m,f}=F_{m,E}-{\int }_{Ef}p\mathrm{d}{V}_m,F_{m,s}=F_{m,E}-{\int }_{Es}p\mathrm{d}{V}_m$$

于是

$$F_{m,f}-F_{m,s}={\int }_{fEs}p\mathrm{d}{V}_m={\oint }_{fEsf}p\mathrm{d}{V}_m>0$$

从而在有限的扰动下, AB,DE上的态可以越过势垒, 过渡到AB',D'E上对应的稳态, 其中AB线段上的状态对应过热液体, DE线段上的状态对应于过冷蒸汽, 或者过饱和蒸汽

对比方程和对应态原理

Van der Waals对比方程

考虑Van der Waals方程, 有

$$(p+\frac{a}{V_m^2})(V_m-b)=RT,V_{m,c}=3b,p_c=\frac{a}{27b^2},T_c=\frac{8a}{27Rb}$$

定义无量纲的对比状态参量$\pi =\frac{p}{p_c},\theta =\frac{T}{T_c},\omega =\frac{V_m}{V_{m,c}}$, 则得到Van der Waals对比方程

$$\left(\pi +\frac{3}{{\omega }^2}\right)(3\omega -1)=8\theta$$

这里不出现任何气体特性常量（如$a,b$）, 因此它是适用于任何气体的普遍方程；

对应态原理

对于任意两个用同一个对比方程$f(\pi ,\omega ,\theta )=0$描述其物态变化的物质, 只要有两个对比状态参量相等, 它们的第三个对比状态参量也一定相等.