Liquid

微观结构

液体是介于气态和固态的一种物态，液体分子间距小，分子力大，不易被压缩；液体分子的排列存在一定的有序性.

我们可以通过X射线衍射来分析液体的微观结构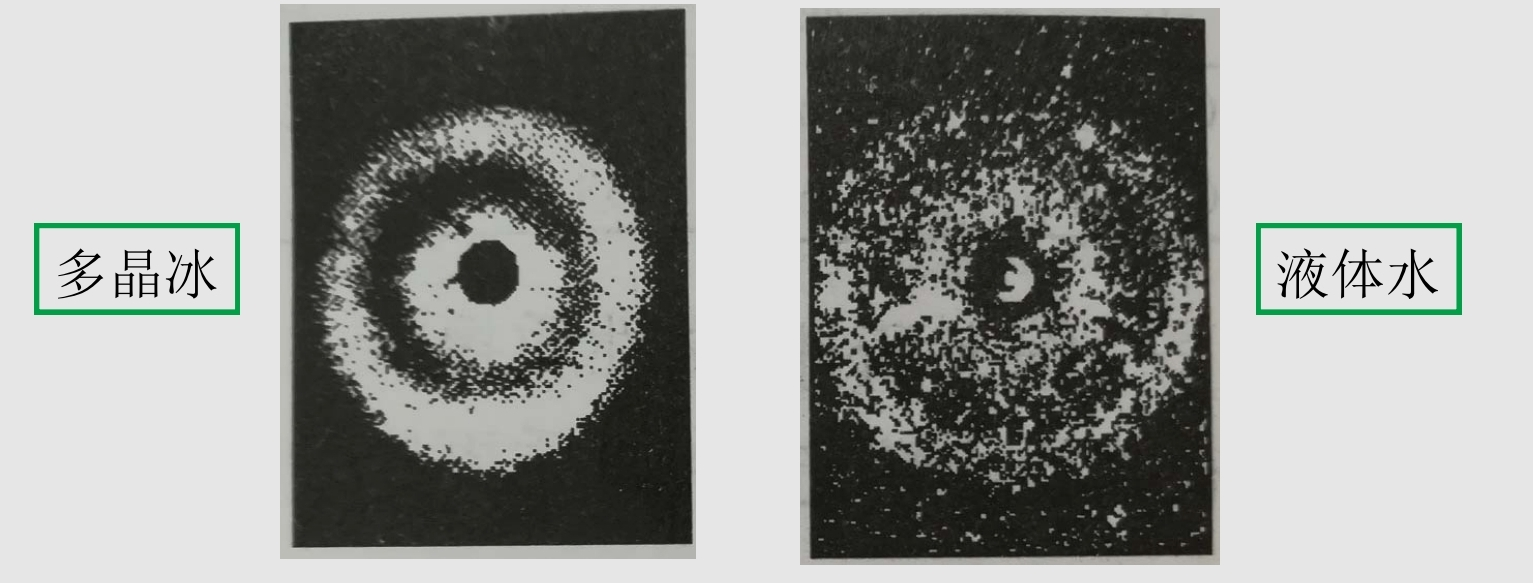： 由衍射图案可以看出，在靠近液体每一个分子的周围，其它分子的分布在一定程度上是有序的，液体中分子分布的有序较为松散. 因而，液体的结构即不同于固体的长程有序，也不同于气体的无序，表现为短程有序、长程无序

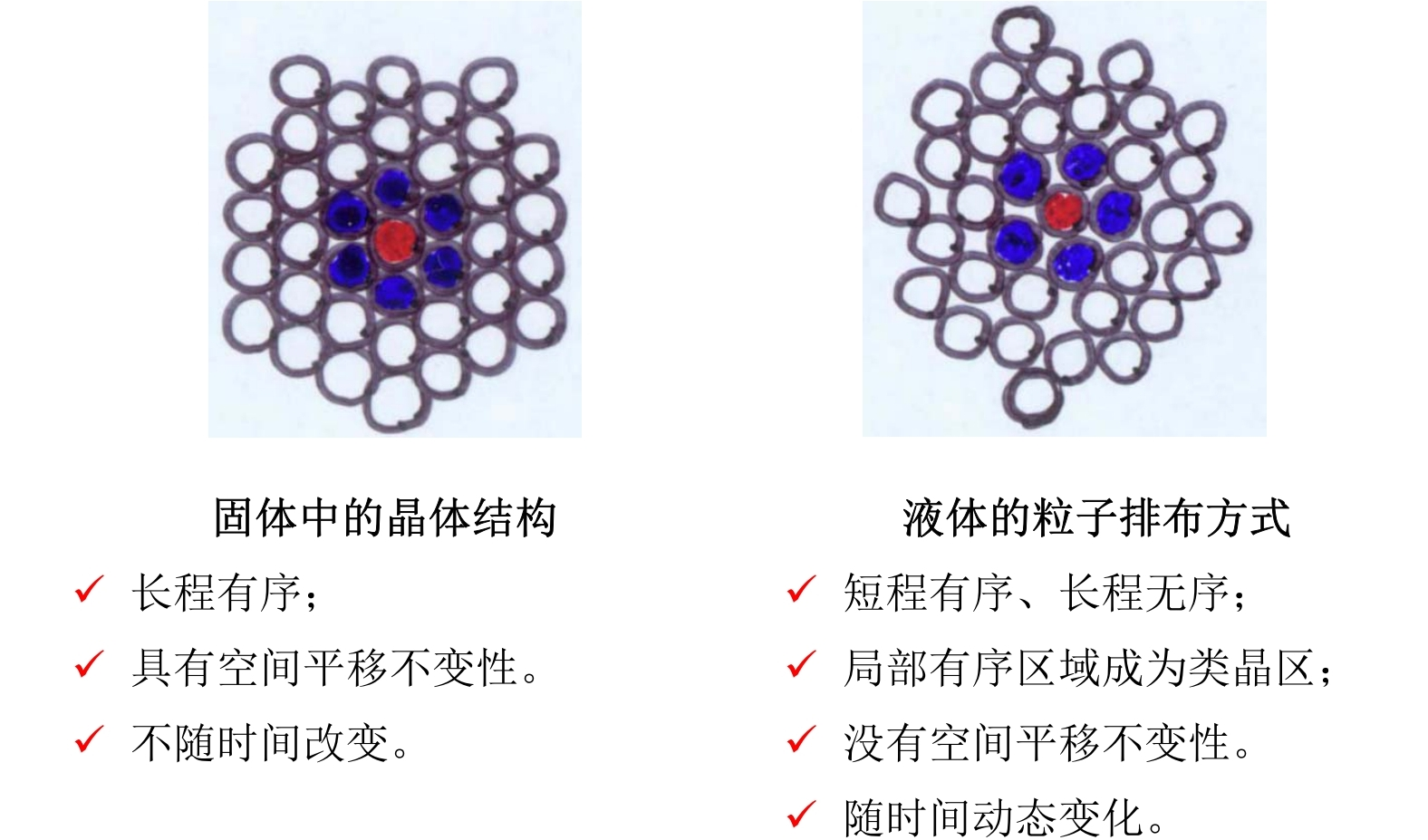
液体的微观结构

虽然液体分子也是一个紧挨着另一个排列，但却不是严格周期性的密堆积，而是一种动态的、较为疏松的短程有序、长程无序的堆积

理论描述

为了定量地描述液体的微观结果，我们定义径向分布函数$g(r)$为包含在$r\sim r+\mathrm{d}r$球形球壳内的平均分子数分布

$$g(r)=4\pi r^2\rho (r)$$

其中径向密度$\rho (r)$定义为$r\sim r+\mathrm{d}r$球形壳层内的平均分子数密度

下图是水分子的径向分布函数 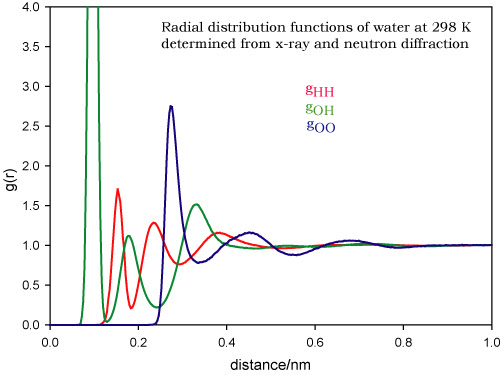可见在距离较大时，径向密度趋于一条水平线，说明液体确实和气体一样长程无序；而在距离较小时，径向密度的规律起伏可以说明起短程有序性

当温度升高时，液体的径向分布函数趋近于气体的径向分布函数（近似于一条直线）；当温度降低时，液体的径向分布函数趋近于相对应固体的径向分布函数

液体分子的热运动

热运动模式

液体分子间的平均距离与固体相当，分子间的相互作用很大； 液体分子的热运动与固体相近，主要是在其平衡位置附近振动（热振动）.

热运动特点

• 液体分子的排列不很规则，分子间相互作用势阱的形状、深度各不相同；同一势阱里（类晶区）粒子的振动模式基本一致；不同势阱里粒子的振动模式各不相同；
• 势阱的形状随时间改变；故粒子振动的中心和相应的振动时间不确定，具有“游牧生活”的特点，“迁移”和“定居”交替.

定居时间

液体分子的定居时间（residence time），通常表示为𝜏，是指液体分子在某个特定区域内（如在某个体积元素或在溶液中的某个位置）停留的平均时间. 其大小由分子间相互作用和热运动的竞争决定.

外力作用下的行为

非晶体的微观结构与液体非常类同，可以认为它是一种没有流动性 （$\tau \to \infty$）的液体. 外力作用于非晶体的时间总是小于$\tau$，所以在外力作用不会流动，而发生弹性形变、脆性断裂等力学现象；

对一般液体，当外力作用时间大于定居时间$\tau$ 时，分子在该时间内可以有很大的移动，故液体将在外力作用下流动；而当外力作用时间远小于液体$\tau$时，液体也会发生弹性形变甚至断裂； **在非常强的冲击力下，液体会像玻璃那样碎裂. **

彻体性质

热容

定压热容

液体分子的热运动形式和固体一样都主要是热振动，因而它们的定压热容接近；但是气体分子的热运动包含振动、转动和平动，故液体和气体的定压热容相差较大

定体热容

固体的定体热容和定压热容基本相等，但是液体的体膨胀系数比固体的大很多，故液体定体热容和定压热容相差较大

又因为液体的体膨胀系数各不相同，故不同液体的定体热容和定压热容之差变化很大

热膨胀

热膨胀现象

热膨胀现象指的是液体在温度升高时体积增大的现象. 其根本原因在于粒子间的平均距离随着温度升高而增加. 这可以通过势能曲线的不对称性来解释：

1. 温度升高时，粒子的热运动加剧，粒子间的平均距离不再仅仅停留在势能最低点，而是围绕这个点进行更大范围的振动.
2. 由于势能曲线在平衡位置右侧（引力区）的斜率较缓，粒子在这个方向上可以较容易地移动更远的距离. 这意味着温度升高后，粒子在这个方向上的位移（即平均距离的增加）更大.
3. 相反，在势能曲线左侧（斥力区），势能上升得非常快，粒子很难在这个方向上移动太远.

因此，随着温度的升高，粒子间的平均距离增大，导致液体体积膨胀.

体膨胀系数

$$\beta =\frac{1}{V}{\left(\frac{\partial V}{\partial T}\right)}_p$$

液体的体膨胀系数一般大于$0$，且比气体的要小；一般比固体的大，但是个别的（如水vs铜）要小

液体的体膨胀系数随温度的升高而增大，随压强的增大而减小；

水的反常膨胀现象：$4^{\circ }\mathrm{C}$左右时密度最大，体积最小. 可用氢键、缔合水分子理论予以解释.

热传导

在没有热对流的情况下，液体中热传导的机制和固体相似

一般液体的导热性很差，这是因为

• 热量主要是通过分子热振动之间的相互联系而逐层传递的，该机制导热能力差，故导热系数很低；
• 液体导热机理与非晶态或不导电的固体相似. 金属液体的导热性相当好，这是因为
• 对于金属液体，热传导过程中能量传递的方式主要是通过自由电子的热运动； 分子的热振动占次要地位；
• 金属液体的导热机理与金属晶体或气体相似，导热系数相当高.

扩散

液体中物质的扩散系数比固体中稍大，但远小于气体中的扩散系数.

液体中物质的扩散需要克服周围分子的吸引（克服所在单元的势井），再在新的位置上和其他分子组成新的单元，所以液体的扩散具有跳跃性的特征，和固体的扩散方式，而和气体的有很大不同

液体的扩散系数反比于定居时间，即$D\propto \frac{1}{\tau }$，液体的扩散系数随温度指数增加，这是因为分子的定居时间可以表示为

$$\tau ={\tau }_0\exp \left(\frac{\Delta W}{k_{B}T}\right)$$

其中$\Delta W$是分子扩散激活能，从而$D=D_0\exp \left(-\frac{\Delta W}{k_{B}T}\right)$

黏性

液体的黏性比气体大，这是因为液体分子受单元中其他分子作用力的束缚，不易在相邻两流层间运动而输送动量

液体的黏度正比于定居时间$\eta \propto \tau$，随温度的升高而指数减小，与气体黏性的行为完全不同（气体的黏度$\eta \propto T^{1/2}$）

表面性质

表面张力系数

表面张力与液面相切、与线段垂直且指向其两侧，可分别用$F$和$F^{\prime }$表示，它们是一对作用力和反作用力

由于线段上各点均有表面张力作用，故线段越长，表面张力越大，有

$$F=\gamma L$$

其中$\gamma$为表面张力系数

表面功

$$\mathrm{d}W=\gamma \mathrm{d}A$$

在绝热条件下，由热力学第一定律

$$\mathrm{d}U=\mathrm{d}W=\gamma \mathrm{d}A⟹\gamma ={\left(\frac{\partial U}{\partial A}\right)}_{\text{绝热}}$$

此时表面张力系数是绝热条件下增加单位表面时所增加的表面内能，即单位表面的表面内能

对于表面系统的可逆等温过程，由自由能的定义

$$\mathrm{d}F=\mathrm{d}W=\gamma \mathrm{d}A⟹\gamma ={\left(\frac{\partial F}{\partial A}\right)}_{\text{等温}}$$

此时表面张力系数是等温条件下增加单位表面时所增加的表面自由能，即单位表面的表面自由能

在外界不对系统做功时，等温情况下，表面自由能减少直到取到最小值，而球形的表面积最小，所以不受任何合外力作用的液体呈球体形状

影响表面张力系数的因素

• 液体成分：密度小、容易挥发的液体 (如液氢和液氦)$\gamma$较小，而金属熔液的$\gamma$则很大；
• 温度：温度越高，$\gamma$越小，实验表明可近似为一线性关系
• 表面(即第二介质)性质：两种互不相溶液体表面的$\gamma$与这两种液体的成分有关；
• 杂质：加入杂质能显著改变液体的$\gamma$，其中使$\gamma$减小的杂质称为表面活性物质 如肥 皂水，醇、酸、醛、酮等有机物质.

表面张力的微观解释

液体分子之间存在Van der Waals力（包括London色散力、偶极-偶极相互作用和氢键等）. 在液体内部，每个分子受到来自周围各个方向的分子引力，这些力相互抵消，导致分子在液体内部处于平衡状态.

然而，在液体的表面层，分子上方没有液体分子，只有空气分子或真空. 因此，表面分子受到的净引力是指向液体内部的. **这种不平衡的力使得表面分子向内拉，从而使液体表面趋向最小化其表面积. **

Young-Laplace方程

如果液面不是平面，液面两边会因为表面张力的作用而产生压强差

$$\Delta p=p_{\text{内}}-p_{\text{外}}=\gamma \left(\frac{1}{R_1}+\frac{1}{R_2}\right)$$

其中$R_1,R_2$是表面上这一点任意两个相互垂直的截口的曲率半径.

提示

对于如肥皂泡这种液面足够薄且两端都是表面的情况，上面的压强差还需要乘以$2$

例子：把压强为大气压$p_0$的空气等温地压缩进肥皂泡内，最后吹成半径为$r$的肥皂泡，假设肥皂泡胀大的过程是等温的，求吹成肥皂泡需要的总功

目标肥皂泡内的气体压强

$$p_1=p_0+2\gamma \left(\frac{1}{r}+\frac{1}{r}\right)=p_0+\frac{4\gamma }{r}$$

则由理想气体等温膨胀做功公式，胀大的过程需要做的总功为

$$A_1=\nu RT\ln \frac{p_1}{p_0}=p_1{V}_1\ln \frac{p_1}{p_0}=p_0\left(1+\frac{4\gamma }{r{p}_0}\right)\cdot \frac{4}{3}\pi r^3\ln \left(1+\frac{4\gamma }{r{\rho }_0}\right)$$

由于$\frac{4\gamma }{r{p}_0}\ll 1$，所以上式可近似为

$$A_1=p_0\cdot 1\cdot \frac{4}{3}\pi r^3\cdot \frac{4\gamma }{r{\rho }_0}=\frac{16}{3}\pi r^2\gamma$$

而要增大肥皂泡内外表面的面积又需要格外做功

$$A_2=\gamma \cdot 2S=8\pi r^2\gamma$$

故总功为

$$A=A_1+A_2=\frac{40}{3}\pi r^2\gamma$$

液面与固体接触处的表面现象

湿润和不湿润现象

不湿润现象：水银在玻璃板上； 湿润现象：水在无油脂的玻璃板上；

湿润或不湿润和液体和固体的性质有关：水银不湿润玻璃，但湿润锌板、铜板和铁板； 水湿润玻璃，但不湿润石蜡；

湿润现象源于附着力和内聚力之间的竞争：附着力是固、液分子之间的相互吸引力；内聚力是液体分子之间的相互吸引力；内聚力大于附着力则不湿润； 附着力大于内聚力则湿润

接触角

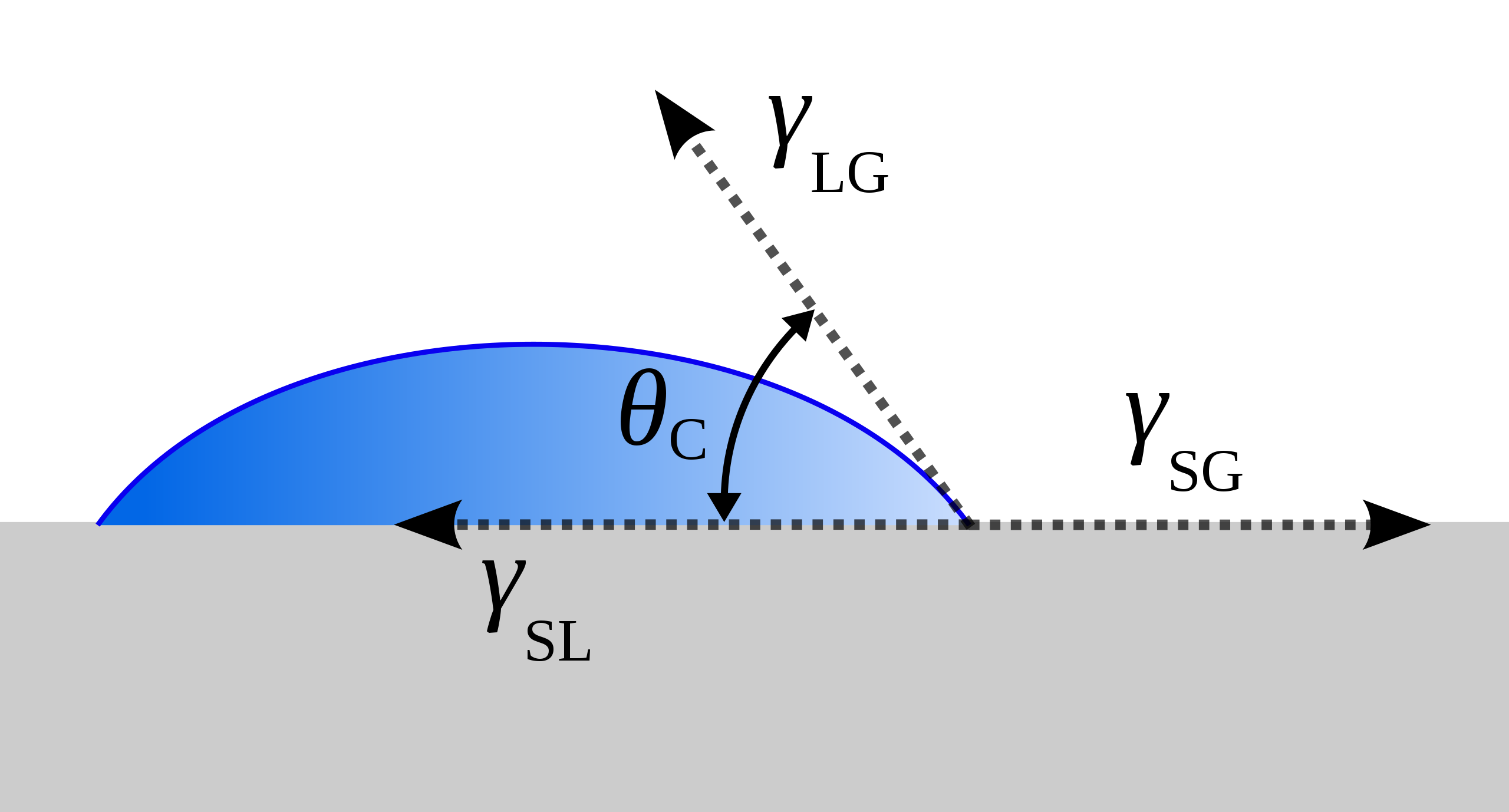
• 内聚力${\gamma }_{LG}$是液体分子之间的吸引力，力图使附着层收缩；
• 附着力${\gamma }_{SG}$是固-液分子之间的吸引力，力图使附着层沿固体表面延展；
• 两种力的竞争使得附着层液体分子所受合力的指向不定 对于接触角有

$$\cos {\theta }_C=\frac{{\gamma }_{SL}}{{\gamma }_{LG}}=\frac{{\gamma }_{\text{solid-liquid}}}{{\gamma }_{\text{liquid-gas}}}$$

如果${\theta }_C>\frac{\pi }{2}$则不湿润；如果${\theta }_C<\frac{\pi }{2}$则润湿

毛细现象

将毛细管插入液体中，管内液面相对于管外液面上升或下降的现象称为毛细现象.

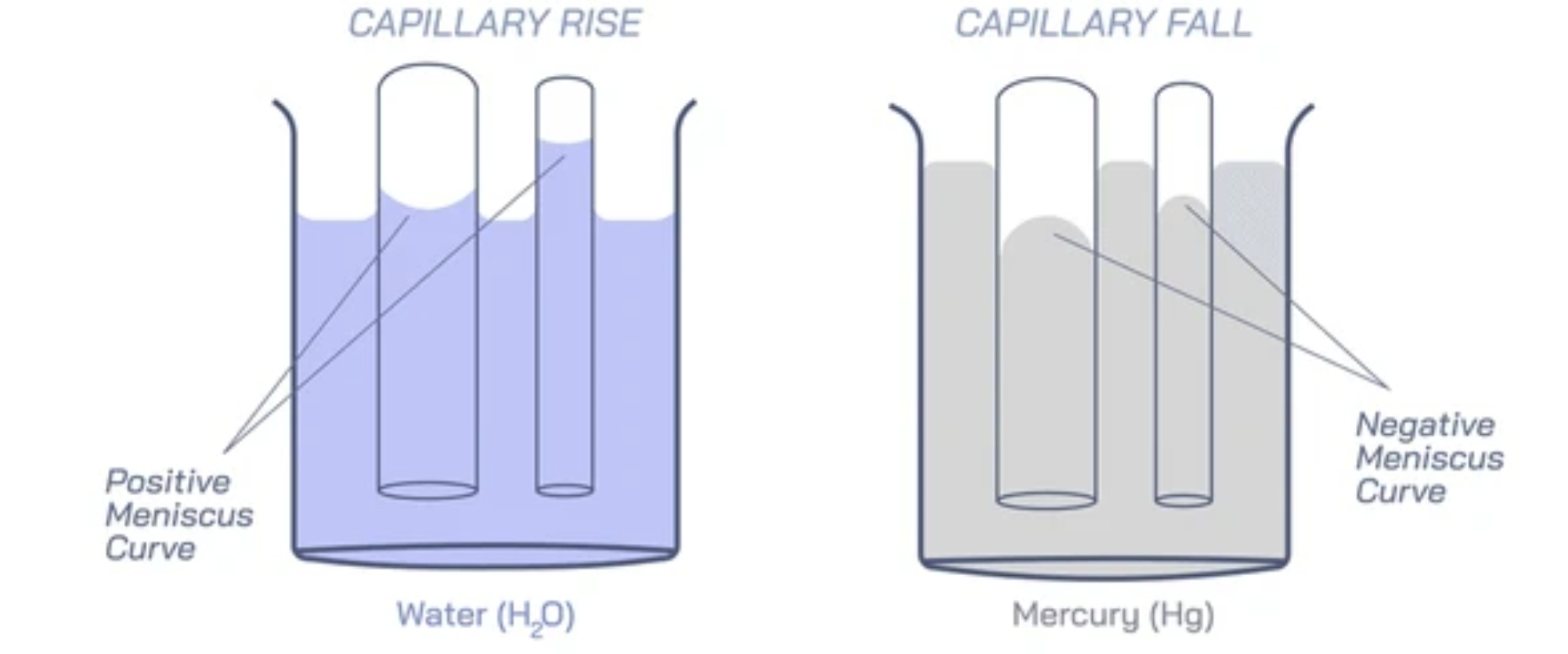
物理解释

内聚力与附着力的竞争引起液面弯曲，弯曲液面内外的压强差导致的管内液体上升或下降.

• 附着力大于内聚力，液体湿润固体，液面下凹：液面内压强小于液面外压强，毛细管内液面上升；
• 附着力小于内聚力，液体不湿润固体，液面上凸：液面内压强大于液面外压强，毛细管内液面下降.

液柱高度的计算

液柱表面两边的压强差$=$液柱产生的压强，则有

$$\gamma (\frac{1}{R_1}+\frac{1}{R_2})=\rho gh$$

如果是半径为$r$的毛细管，凹液面的两个曲率半径$R_1=R_2=\frac{r}{\cos \theta }$，于是便有

$$h=\frac{2\gamma \cos \theta }{rg\rho }$$

如果是相隔为$d$的平行板，则有$R_1=\frac{d}{2\cos \theta },R_2=+\infty$，于是便有

$$h=\frac{2\gamma \cos \theta }{dg\rho }$$