Householder Transformation and Matrix

A Householder transformation (also known as a Householder reflection or elementary reflector) is a linear transformation that describes a reflection about a plane or hyperplane containing the origin.

Definition

The reflection hyperplane can be defined by its normal vector, a unit vector $\mathbf{v}$ that is orthogonal to the hyperplane. The reflection of a point $\mathbf{x}$ about this hyperplane is the linear transformation:

$$Q_{\mathbf{v}}(\mathbf{x})=\mathbf{x}-2(\mathbf{x}|\mathbf{v})\mathbf{v}$$

or written as the matrix form

$$H=E-2\mathbf{v}{\mathbf{v}}^t$$

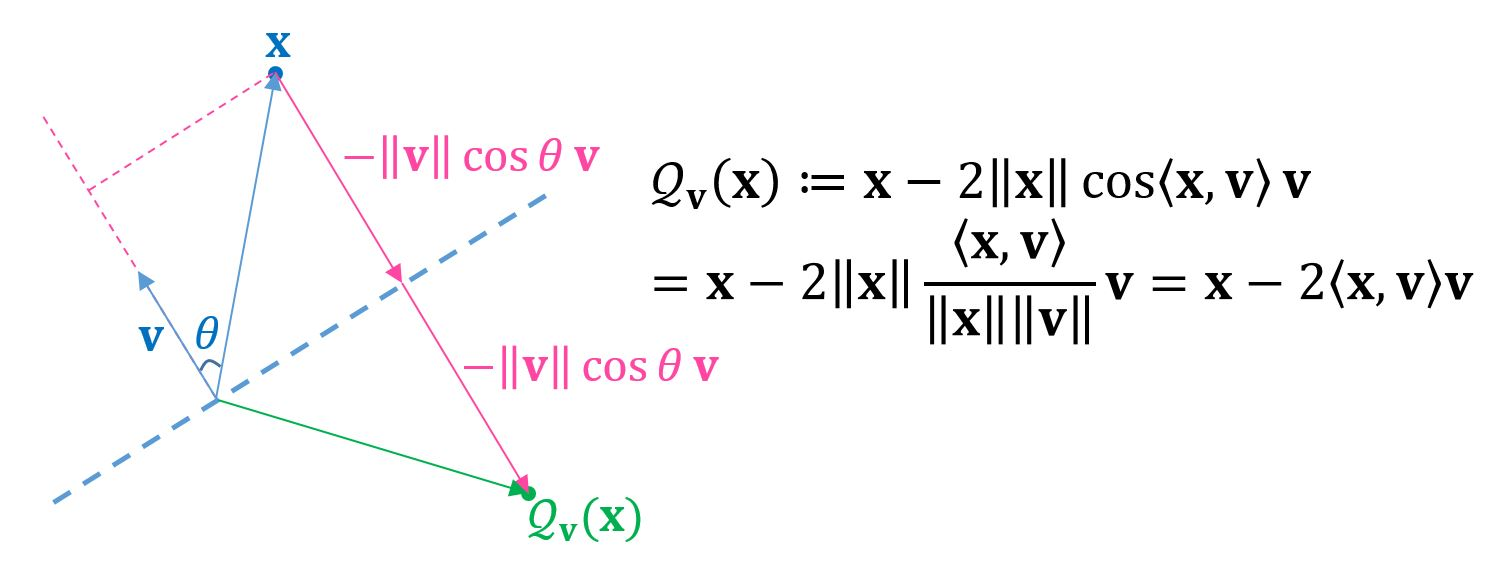
Properties

It is easy to verify that $H$ is

• orthogonal ($H^{t}H=E$)
• symmetric ($H^t=P$)
• involutory ($P^2=E$) where the last property follows from the first two.

$H$ has an eigenvalue $-1$ with the eigenvector $\mathbf{v}$, since $H\mathbf{v}=-\mathbf{v}$. And $H$ has $n-1$ eigenvalues $1$ with eigenvectors any set of $n-1$ linearly independent vectors orthogonal to $\mathbf{v}$

$H$ has trace $n-2$ and determinant $-1$, as can be derived directly or deduced from the facts that the trace is the sum of the eigenvalues and the determinant is the product of the eigenvalues.