Attention Is All You Need

Why Transformer

Limitations of RNNs

• Encoding bottleneck: RNNs encode a lot of content as during the time steps but only output a single context vector at the last time step
• Slow: no way to parallelize the recurrent computing steps
• Not long memory: even LSTMs cannot effectively learning very long sequential data

Transformer's Solution

• Parallelization: concatenate all the inputs together and do the computation at the same time, use positional encoding to save the ordering information
• Attention Mechanism: directly access the previous inputs to achieve longer memory

Model Architecture

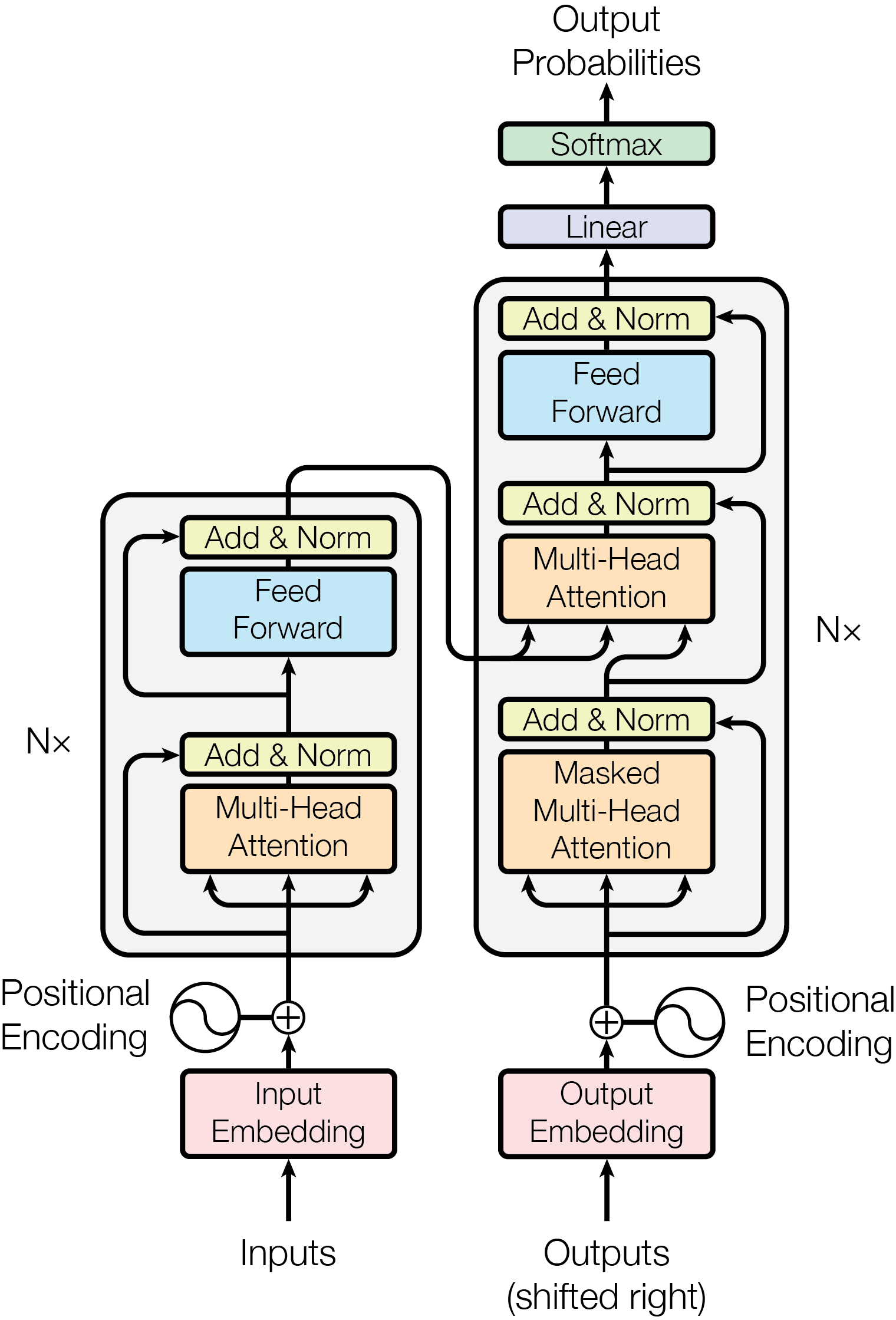
Input / Output Embedding

Convert token to vectors, see Word Embedding. The weights of the embedding layer are initialized with random numbers and will be optimized during training process.

Positional Encoding

Due to the need of parallelization, the model takes in all the sequential inputs at once so the ordering information is lost. Therefore, the model uses a sinusoidal function to generate positional encodings, which are added (residual connection) to the input embeddings to save this positional ordering information. The formulas for the positional encoding $\mathrm{PE}$ at position $\mathrm{pos}$ and dimension $i$ are defined as follows:

$$\begin{array}{c}\mathrm{PE}(\mathrm{pos},2i)=\sin \left(\frac{\mathrm{pos}}{10000^{2i/d_{\mathrm{model}}}}\right)\\ \mathrm{PE}(\mathrm{pos},2i+1)=\cos \left(\frac{\mathrm{pos}}{10000^{2i/d_{\mathrm{model}}}}\right)\end{array}$$

Here $d_{\mathrm{model}}$ is the dimensionality of the embeddings. The use of both sine and cosine functions allows the model to capture different frequencies, which helps in representing various positional relationships.

Attention Mechanism

Dot-Product Attention

The transformer applies dot-product attention to compute the alignment scores between a set of queries and keys. For a given query $Q$ and a set of keys $K$, the attention scores are computed using the dot product

$$\text{scores}=Q{K}^T$$

This results in a matrix of scores that reflects how well each query aligns with each key.

In addition, To prevent the dot products from growing too large, especially when the dimension of the keys (denoted as $d_k$​) is high, the scores are scaled down by the square root of $d_k$:

$$\text{scaled scores}=\frac{Q{K}^T}{\sqrt{d_k}}$$

This scaling helps maintain stable gradients during training.

Finally, the scaled scores are then passed through a softmax function to convert them into attention weights, which ensures that the weights are normalized and sum to one. We gain the output from multiplying the weights by the values $V$:

$$\text{Attention}(Q,K,V)=\text{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

Multi-Head Attention

Multi-head attention operates by running multiple attention mechanisms in parallel. Each of these mechanisms is referred to as an "attention head." The inputs to the attention mechanism—queries ($Q$), keys ($K$), and values ($V$)—are split into multiple subspaces, and each head processes its own set of $Q$, $K$, and $V$ matrices independently. The outputs from all heads are then concatenated and linearly transformed to produce the final output of the multi-head attention layer

The mathematical formulation of multi-head attention can be described as follows:

$$\text{MultiHead}(\text{Q},\text{K},\text{V})=\text{Concat}({\text{head}}_1,\dots ,{\text{head}}_h){\text{W}}_0$$

where each head is computed as:

$${\text{head}}_i=\text{Attention}(\text{Q}{\text{W}}_i^Q,\text{K}{\text{W}}_i^K,\text{V}{\text{W}}_i^V)$$

Here, ${\text{W}}_i^Q,{\text{W}}_i^K,{\text{W}}_i^V$ are learnable parameter matrices corresponding to the queries, keys, and values for each head, respectively.

Normalization

See Layer Normalization